浙教版八年级上册第1章 三角形的初步知识1.5 三角形全等的判定多媒体教学课件ppt

这是一份浙教版八年级上册第1章 三角形的初步知识1.5 三角形全等的判定多媒体教学课件ppt，共23页。PPT课件主要包含了复习引入，定理的证明，练习1，练习2，等边三角形，等边三角形判定探索，等边三角形性质探索，练习3，练习4，练习5等内容，欢迎下载使用。
1.等腰三角形的两腰相等.
2.等腰三角形的两个底角相等,（简称“等边对等角”）.
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合.（简称“三线合一”）
4.等腰三角形是轴对称图形,对称轴是底边的中垂线.
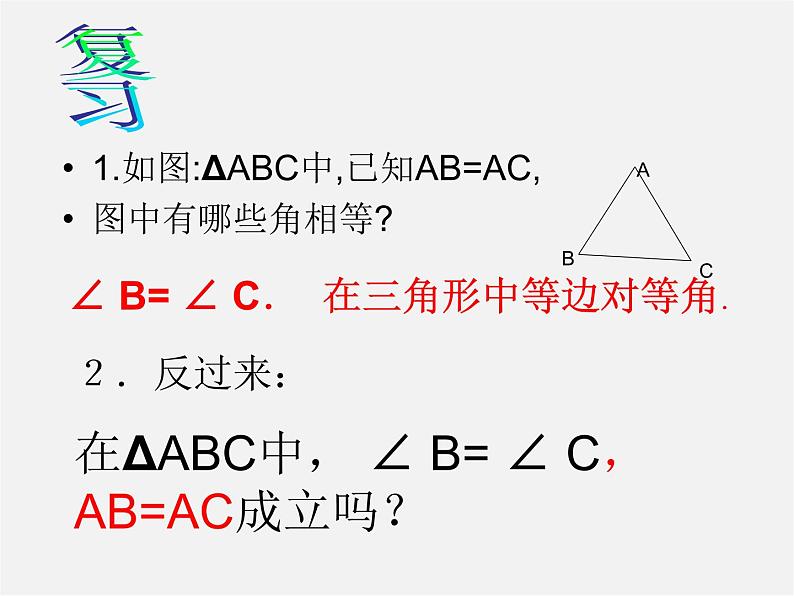
1.如图:ΔABC中,已知AB=AC,图中有哪些角相等?
∠ B= ∠ C． 在三角形中等边对等角．
２．反过来：在ΔABC中， ∠ B= ∠ C， AB=AC成立吗？
1，作一个三角形，有两个角相等，这两个角所对的边是否相等？
在ΔABC中，∠B=∠C作∠BAC的平分线交BC于D，则∠ 1=∠2，又∠B=∠C，由三角形内角和的性质得∠ADB=∠ADC，沿直线
AD折叠∠ADB=∠ADC ，∠1= ∠2，所以射线DB与射线DC重合，射线AB与射线AC重合，从而点B与点C重合，因此AB=AC
等腰三角形有以下的判定方法：
　如果一个三角形有两个角相等，那么这个三角形是等腰三角形．简单地说；在同一个三角形中，　　　　　等角对等到边．
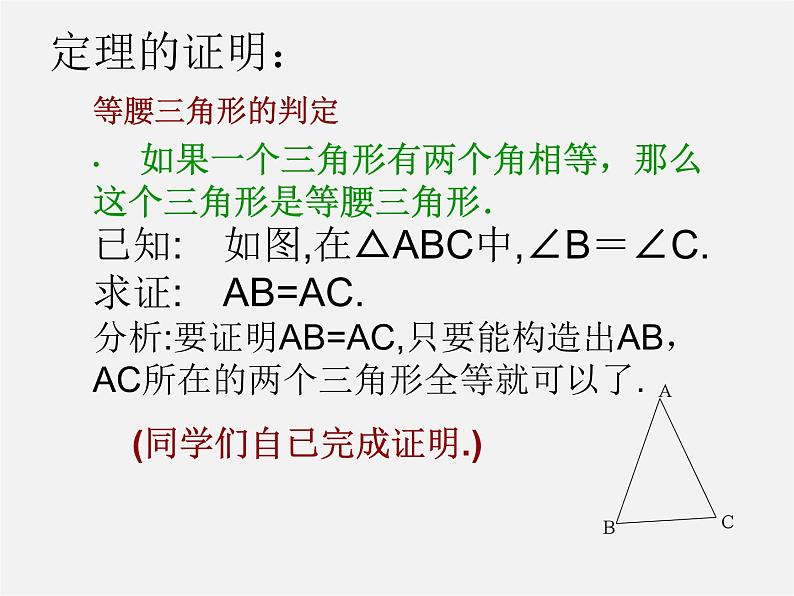
等腰三角形的判定　　如果一个三角形有两个角相等，那么这个三角形是等腰三角形．已知:　如图,在△ABC中,∠B＝∠C.求证:　AB=AC.分析:要证明AB=AC,只要能构造出AB，AC所在的两个三角形全等就可以了. (同学们自已完成证明.)
在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?
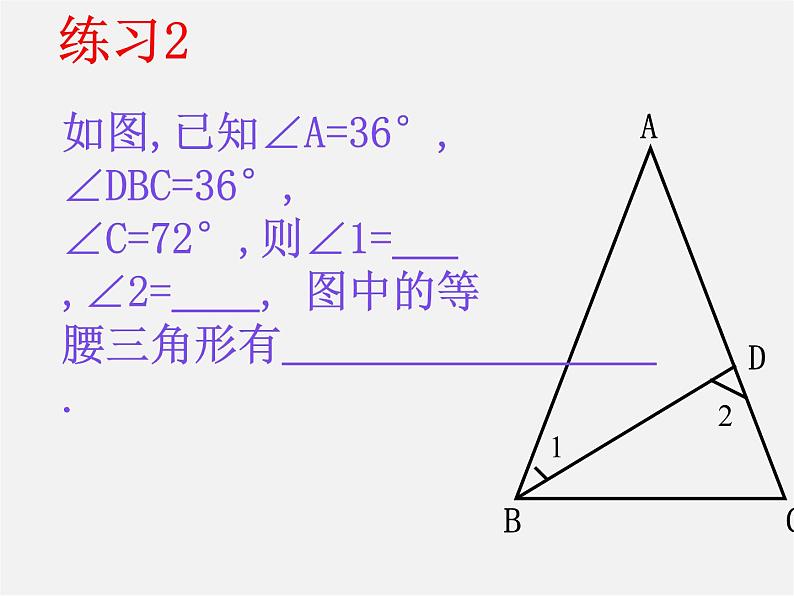
如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .
在等腰三角形中，有一种特殊的情况，就是底边与腰相等，这时，三角形三边相等。
我们把三条边都相等的三角形叫做等边三角形（正三角形）。
1.三个内角都等于60 °的三角形是等边三角形. ∵∠A=∠B=∠C=60 ° ∴AB=AC=BC (为什么) ∴三角形△ABC是等边三角形.
2.有一个内角等于60 °的等腰三角形是等边三角形. 假若AB=AC，则∠ B= ∠ C 当顶角∠A=60 °时, ∠ B= ∠ C= 60 ° ∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形. 当底角∠ B= 60时, ∠ C=60 °, ∠A=180 —(60° +60 °)=60. ° ∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.2.三个内角都等于60 °的三角形是等边三角形.3.有一个内角等于60 °的等腰三角形是等边三角形.
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3(1)求BEC的度数.(2) △ DEF为等边三角形吗?为什么?
例１．一次数学实践活动的内容是测量河宽，如图，即测量Ａ，Ｂ之间的距离．同学们想出了许多方法，其中小聪的方法是：从点Ａ出发，沿着与直线ＡＢ成６０ °角的ＡＣ方向前进至Ｃ，在Ｃ处测得Ｃ＝30° ．量出ＡＣ的长，它就是河宽（即Ａ，Ｂ之间的距离）．这个方法正确吗？请说明理由．解：小聪的测量方法正确．理由如下：∵ ∠ＤＡＣ＝ ∠Ｂ＋ ∠Ｃ（三角形的外角的性质）∴ ∠ＡＢＣ＝ ∠ＤＡＣ－ ∠Ｃ＝６０ ° －３０ ° ＝３０ °∴ ∠ＡＢＣ＝ ∠Ｃ∴ＡＢ＝ＡＣ（在一个三角形中，等角对等边．）
上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得∠NAC=40°， ∠NBC=80°求从B处到灯塔C的距离
解：∵∠NBC=∠A+∠C∴∠C=80°- 40°= 40° ∴ BA=BC（等角对等边）∵AB=20（12-10）=40∴BC=40答：B处到达灯塔C40海里
例２.如果三角形一个角的外的角平分线平行于三角形的第三边，那么这个三角形是等腰三角形吗？为什么？
解：因为AD∥BC，所以∠1=∠B,∠2=∠C.因为∠1=∠2，∠B=∠C.因此AB=AC，即ΔABC的是等腰三角形.
例３．如图，ＢＤ是等腰三角形ＡＢＣ的底边ＡＣ上的高，ＤＥ∥ＢＣ，交ＡＢ于点Ｅ．判断△ＢＤＥ是不是等腰三角形，并说明理由．（请你自已完成说理过程）
1.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?
2.如图，在等腰△ABC中，AB=AC，两底角的平分线BE和CD相交于点O，那么△OBC是什么三角形？为什么？
有两边相等的三角形是等腰三角形
1.两腰相等
思考1:如图,在△ABC中，已知∠ABC=∠ACB，BF平分∠ABC，CF平分∠ACB,请想想看,由以上条件,你能推导出什么结论?并说明理由.
与同伴交流你在探索思路的过程中的具体做法.
下例各说法对吗？为什么？
等腰三角形两底角的平分线相等.等腰三角形两腰上的中线相等.等腰三角形两腰上的高相等.