





还剩11页未读,
继续阅读
初中数学3.2 不等式的基本性质示范课ppt课件
展开
这是一份初中数学3.2 不等式的基本性质示范课ppt课件,共19页。PPT课件主要包含了合作学习,则ac,比较大小,不等式的基本性质3,练一练,即2a<a,体会分享等内容,欢迎下载使用。
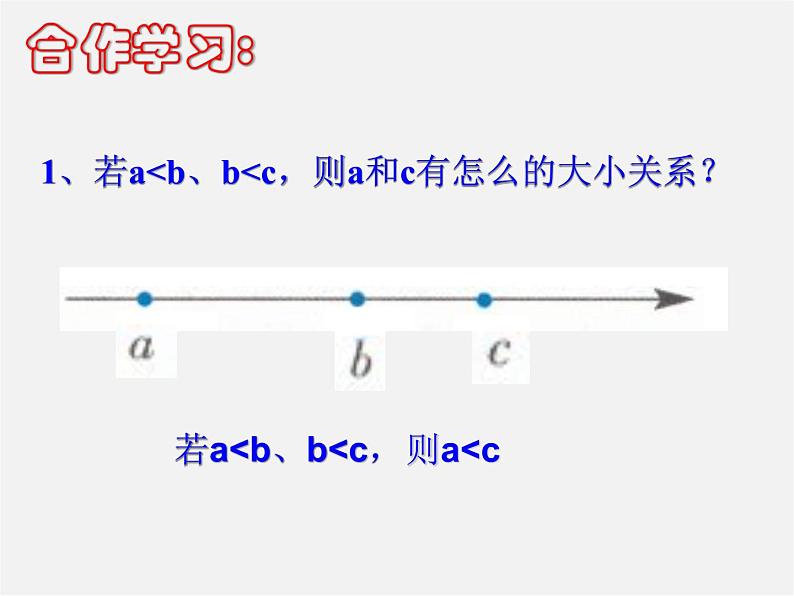
1、等式中, 如果a=b b=c, 那么a c,
2、观察下面这几个式子,完成下面的填空 ∵ a=b ∴ a±3 = b±3 a±(2x+y)=b±(2x+y)等式的基本性质1:等式的两边都加上(或减去)_______或______,等式仍然成立。
3、继续观察 ∵ a=b ∴ 3a=3b a/3 =b/3 等式的基本性质2: 等式的两边都乘以(或除以)___________(除数不能为零),等式仍然成立。
(二)自学、相信自己 1、等式具有传递性; 那么不等式是否有传递性? 若a 不等式的两边都加上(或减去)_________,所得的不等式仍成立。 不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立; 不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立。
1、若a不等式的基本性质1: 若a不等式的基本性质2: 不等式的两边都加上(或减去)同一个数,所得的不等式仍成立。如果a>b,那么a+c>b+c, a-c>b-c如果a<b,那么a+c<b+c, a-c<b-c
5 > 3 5 > 35×1( )3×1, 5×(-1)( )3×(-1)5×2( )3×2, 5×(-2)( )3×(-2)5×3( )3×3, 5×(-3)( )3×(-3)5×4( )3×4, 5×(-4)( )3×(-4)… …
小聪同学在完成上题后,归纳认为:不等式的两边都乘以(或除以)同一个数,所得到的不等式仍成立。你认为对吗?为什么?
1、不等式的两边都乘以(或除以)同一个正数, 所得的不等式仍成立;
2、不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立.
如果a>b,且c>0,那么ac>bc, 如果a<b,且c<0,那么ac<bc,
奇怪,乘正数乘负数,怎么就没有零呢?为什么?
1、若a<b,b<2a-1,则a______2a-1
5、 若a <b,则2-a_____2-b
4、若-a<b,则a_______ -b
选择恰当的不等号填空,并说出理由。
2、若a>-b,则a+b___ b-b ,a+b___0
3、若4a<4b,则a_______ b
例1:已知a<0,试比较2a与a的大小.
解法1: ∵ 2 > 1,a<0 ∴ 2a <a(不等式的基本性质3)
解法2: 在 数轴上分别表示2a与a的点(a<0 )
解法3: ∵ a<0
∵ 2a位于a的左边, ∴ 2a <a
∴ a+a<0+a (不等式的基本性质2)
3.下列各题的横线上填入不等号,使不等式成立.并说明是根据哪一条不等式基本性质. (1)若a-3<9,则 a ______12; (2)若-a<10,则a______ -10; (3)若0.5a>-2, 则a ______-4; (4)若-a>0, 则 a______0。
例4:某品牌计算机键盘的单价在60元至70元之间,买3个这样的键盘需要多少钱?(用适当的不等式表示)
说能出你这节课的收获和体验让大家与你分享吗?
1、等式中, 如果a=b b=c, 那么a c,
2、观察下面这几个式子,完成下面的填空 ∵ a=b ∴ a±3 = b±3 a±(2x+y)=b±(2x+y)等式的基本性质1:等式的两边都加上(或减去)_______或______,等式仍然成立。
3、继续观察 ∵ a=b ∴ 3a=3b a/3 =b/3 等式的基本性质2: 等式的两边都乘以(或除以)___________(除数不能为零),等式仍然成立。
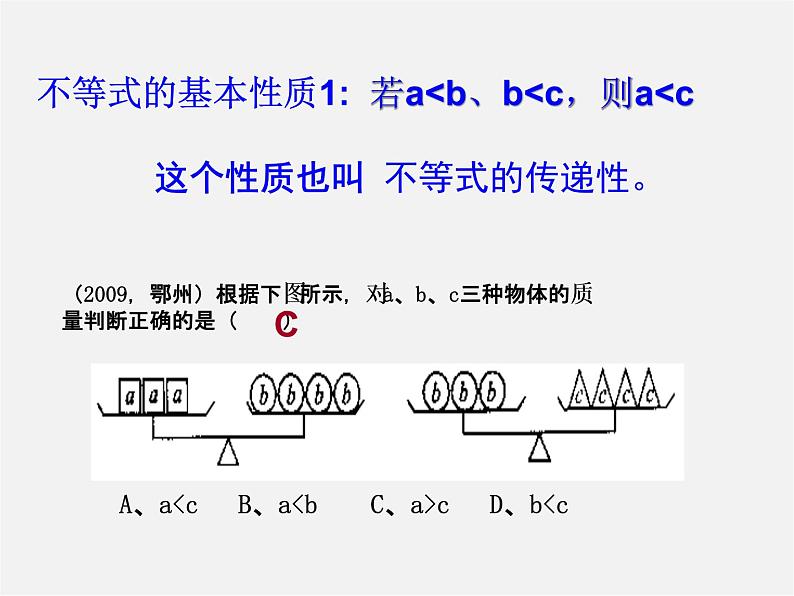
(二)自学、相信自己 1、等式具有传递性; 那么不等式是否有传递性? 若a
1、若a
5 > 3 5 > 35×1( )3×1, 5×(-1)( )3×(-1)5×2( )3×2, 5×(-2)( )3×(-2)5×3( )3×3, 5×(-3)( )3×(-3)5×4( )3×4, 5×(-4)( )3×(-4)… …
小聪同学在完成上题后,归纳认为:不等式的两边都乘以(或除以)同一个数,所得到的不等式仍成立。你认为对吗?为什么?
1、不等式的两边都乘以(或除以)同一个正数, 所得的不等式仍成立;
2、不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立.
如果a>b,且c>0,那么ac>bc, 如果a<b,且c<0,那么ac<bc,
奇怪,乘正数乘负数,怎么就没有零呢?为什么?
1、若a<b,b<2a-1,则a______2a-1
5、 若a <b,则2-a_____2-b
4、若-a<b,则a_______ -b
选择恰当的不等号填空,并说出理由。
2、若a>-b,则a+b___ b-b ,a+b___0
3、若4a<4b,则a_______ b
例1:已知a<0,试比较2a与a的大小.
解法1: ∵ 2 > 1,a<0 ∴ 2a <a(不等式的基本性质3)
解法2: 在 数轴上分别表示2a与a的点(a<0 )
解法3: ∵ a<0
∵ 2a位于a的左边, ∴ 2a <a
∴ a+a<0+a (不等式的基本性质2)
3.下列各题的横线上填入不等号,使不等式成立.并说明是根据哪一条不等式基本性质. (1)若a-3<9,则 a ______12; (2)若-a<10,则a______ -10; (3)若0.5a>-2, 则a ______-4; (4)若-a>0, 则 a______0。
例4:某品牌计算机键盘的单价在60元至70元之间,买3个这样的键盘需要多少钱?(用适当的不等式表示)
说能出你这节课的收获和体验让大家与你分享吗?













