数学八年级上册1.3 证明教学演示ppt课件

这是一份数学八年级上册1.3 证明教学演示ppt课件，共22页。PPT课件主要包含了证明命题的一般步骤，议一议，你有没有其他的证法，三角形的外角，∠ACD∠A，∠ACD∠B，做一做，课堂小结，拓展提高等内容，欢迎下载使用。

(1) 根据题意,画出图形；
(2) 分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；
(3) 在“证明”中写出推理过程.
　　依据思路，运用数学符号和数学语言条理清晰地写出证明过程；检查表达过程是否正确、完善.
对于三角形，我们已经有哪些认识？
三角形的三个内角的和等于180°.
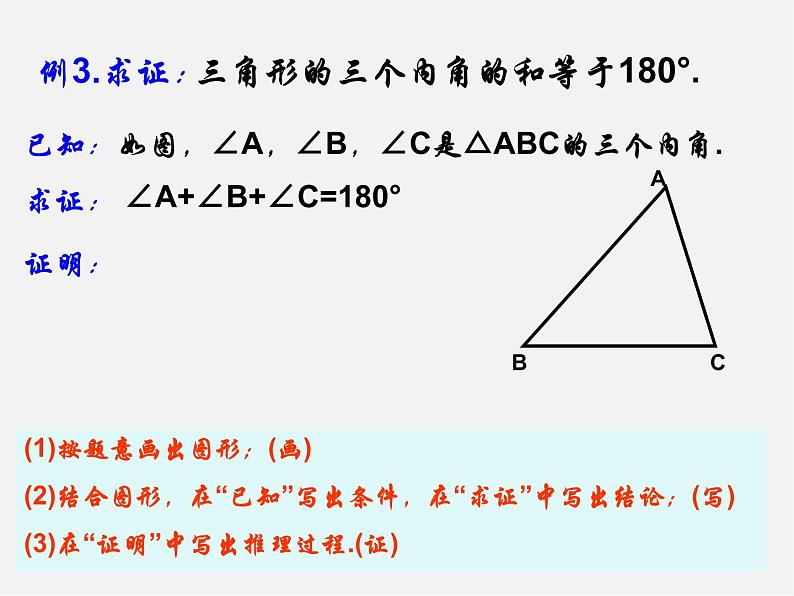
如图，∠A，∠B，∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
(1)按题意画出图形；(画)(2)结合图形，在“已知”写出条件，在“求证”中写出结论；(写)(3)在“证明”中写出推理过程.(证)
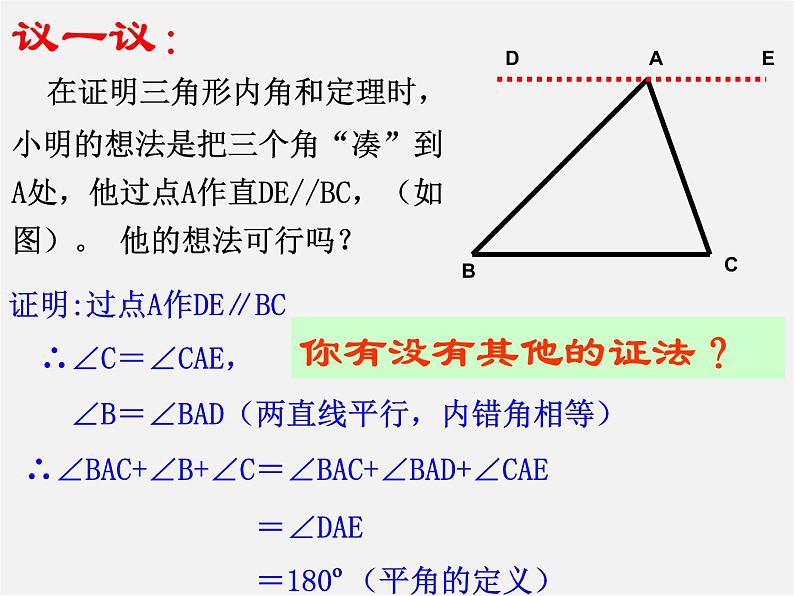
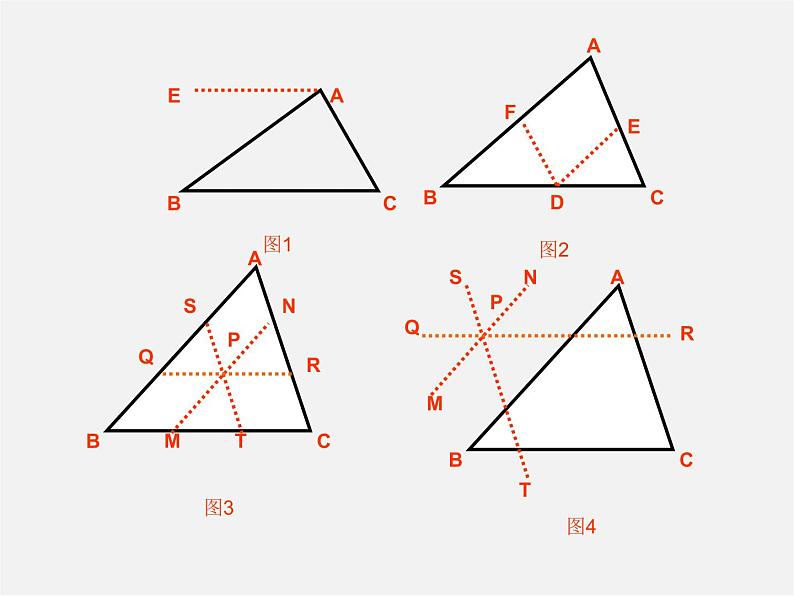
在证明三角形内角和定理时，小明的想法是把三个角“凑”到A处，他过点A作直DE//BC，（如图）。 他的想法可行吗？
证明:过点A作DE∥BC ∴∠C＝∠CAE， ∠B＝∠BAD（两直线平行，内错角相等） ∴∠BAC+∠B+∠C＝∠BAC+∠BAD+∠CAE　 ＝∠DAE ＝180º（平角的定义）
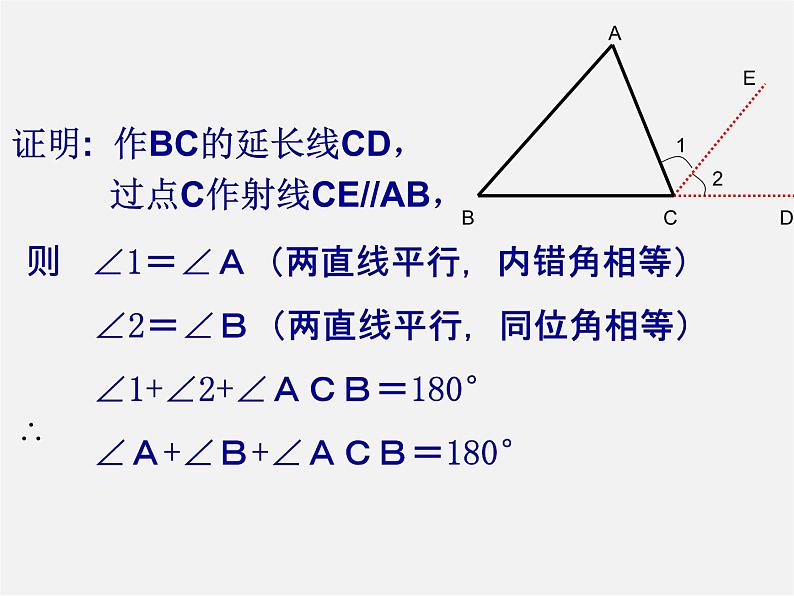
证明: 作BC的延长线CD， 过点C作射线CE//AB，
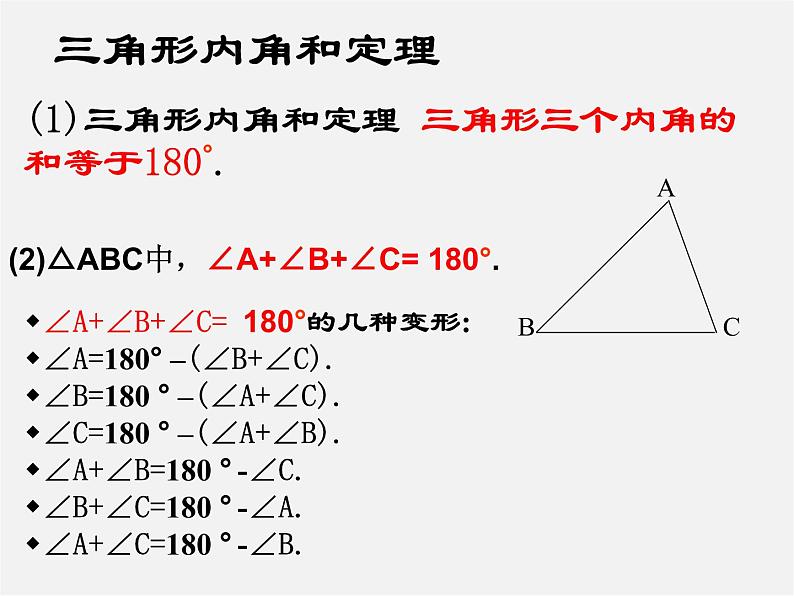
(1)三角形内角和定理 三角形三个内角的 和等于180°.
∠A+∠B+∠C= 180°的几种变形:∠A=180° –(∠B+∠C).∠B=180 ° –(∠A+∠C).∠C=180 ° –(∠A+∠B).∠A+∠B=180 ° -∠C.∠B+∠C=180 ° -∠A.∠A+∠C=180 ° -∠B.
(2)△ABC中，∠A+∠B+∠C= 180°.
辅助线是为了证明需要在原图上添画的线.（辅助线通常画成虚线）它的作用是把分散的条件集中，把隐含的条件显现出来，起到牵线搭桥的作用.添加辅助线，可构造新图形，形成新关系，找到联系已知与未知的桥梁，把问题转化，但辅助线的添法没有一定的规律，要根据需要而定,平时做题时要注意总结.
如图，∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的角，这样的角叫做该三角形的外角。
三角形内角和定理：三角形的三个内角的和等于180°.
三角形的一个外角等于和它不相邻的两个内角的和.
如图，∠ACD是△ABC的一个外角
∠ACD =∠A+∠B
三角形的一个外角大于任何一个和它不相邻的内角.
1.在△ABC中，以A为顶点的一个外角为120°∠B=35°,∠C= .
2.如图，比较∠1与∠2+∠3的大小.
例4 已知：如图，∠B+ ∠D =∠BCD， 求证：AB∥DE　　　　
1.已知：如图，∠B+∠C+∠D=360° 求证：AB∥CD.
如图，在五角星图形中，求：∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。
1. 本节课你学会了什么？ 2. 需要注意什么？你还有什么疑惑吗？
3.你对自己的表现满意吗？为什么？
已知：如图，已知AD是△ABD 和△ACD 的公共边求证：∠BDC=∠BAC+∠B+∠C
如图，已知AD是△ABD 和△ACD的公共边.求证： ∠BDC=∠BAC+∠B+∠C
∵∠1=∠3+∠B，∠2=∠4+∠C
∴∠1+∠2=∠3+∠B+∠4+∠C
即∠BDC=∠BAC+∠B+∠C
如图，已知AD是△ABD 和△ACD的公共边.求证： ∠BDC=∠BAC+∠B+∠C
证法一：∵在△ABD中, ∠1＝180°－∠B－∠3 （三角形内角和定理） 在△ADC中, ∠2＝180°－∠C－∠4 （三角形内角和定理） 又∵∠BDC＝360°－∠1－∠2（周角定义） ∴∠ BDC ＝360°－（ 180°－∠B－∠3 ）－（ 180°－∠C－∠4 ）＝ ∠B+∠C+∠3+∠4. 又 ∵ ∠BAC ＝ ∠3+∠4, ∴ ∠ BDC ＝ ∠B+∠C+ ∠BAC （等量代换）