初中数学人教版八年级上册13.3.1 等腰三角形第2课时精练

这是一份初中数学人教版八年级上册13.3.1 等腰三角形第2课时精练，共5页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．如图（1），△ABC中，AB=AC，DE是AB的中垂线，△BCE的周长
为14，BC=6，则AB的长为 。
2．在△ABC中，∠A=90°，BD为角平分线，DE⊥BC于E，且E恰为
BC中点，则∠ABC等于 。
3．等腰三角形的底边长为5cm，一腰上中线把其周长分成两部分之差为3cm，则腰长为 。
4．如果等腰三角形的顶角是它的一个底角的2倍，这个三角形按角分类应为 。
D
A
B
C
图（2）
5．△ABC中，AB=AC，∠A+∠B=115°，则∠A= ，∠B= 。
6．等腰三角形底角的一个外角为100°，则它的顶角为 。
7．如图（2），AB∥CD，AC平分∠DAB，若∠D=136°，则
∠DCA= 。
A
B
C
D
E
图（3）
8．如图（3），在△ABC中，∠ABC=70°，∠ACB=50°，D、C、B、E
在一条直线上，且DB=AB，CE=AC，则∠E= ，
O
A
B
M
图（4）
∠D= ，∠DAE= 。
9．如图（4），已知∠AOB=40°，OM平分∠AOB，MA⊥OA于A，
MB⊥OB于B，则∠MAB的度数为 。
10．等腰三角形的周长为24cm，其中一边长为7cm，则另外两条
边为 。
二、解答题
1．如图（5），△ABC中，∠A=80°，BD=BE，CD=CF，求∠EDF的度数。
A
B
C
D
F
E
图（5）
A
B
D
C
F
图（6）
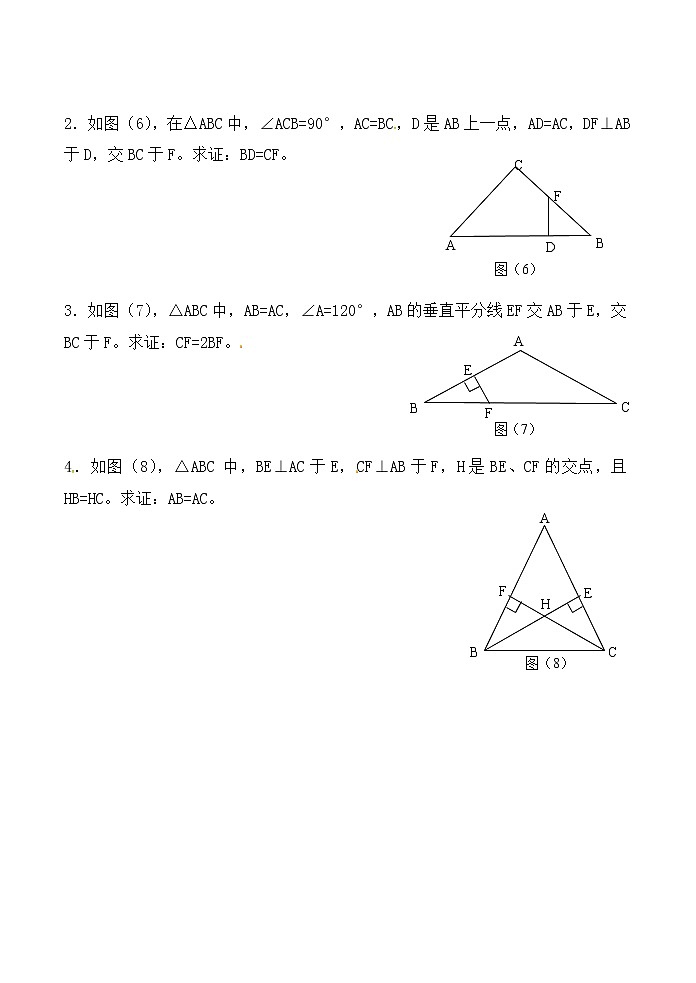
2．如图（6），在△ABC中，∠ACB=90°，AC=BC，D是AB上一点，AD=AC，DF⊥AB于D，交BC于F。求证：BD=CF。
A
B
C
F
E
图（7）
3．如图（7），△ABC中，AB=AC，∠A=120°，AB的垂直平分线EF交AB于E，交BC于F。求证：CF=2BF。
A
B
C
F
E
图（8）
H
4．如图（8），△ABC 中，BE⊥AC于E，CF⊥AB于F，H是BE、CF的交点，且HB=HC。求证：AB=AC。
参考答案
一、1． 8
2．60°
3．8cm
4．直角三角形
5．50°、65°
6．20°或80°
7．22°
8．25° 35° 110°
9．20°
10．7cm、10cm或8.5cm、8.5cm
A
B
C
D
F
E
图（5）
1
2
3
4
二、1．证明：∵∠A+∠B+∠C=180°，∠A=80°
∴∠B+∠C=100°
∵BD=BE CD=CF
∴∠1=∠2 ∠3=∠4
∵∠B+∠1+∠2=180°∠C+∠3+∠4=180°
∴∠2= （180°—∠B）∠4= （180°—∠C）
∵∠2+∠EDF+∠4=180°
∴∠EDF=180°—∠2—∠4=180°— （180°—∠B）— （180°—∠C） =∠B+∠C=100°
2．证明：连结AF。
∵DF⊥AB
∴∠ADF=90°
在Rt△ACF和△ADF中
AF=AF
AC=AD
∴Rt△ACF≌Rt△ADF（HL）
∴CF=DF
∵AC=BC
∴∠A=∠B
∵∠A+∠B+∠ACB=180°，∠ACB=90°
∴∠B=45°
A
B
D
C
F
图（6）
∵∠DFB+∠B+∠BDF=180°
∴∠DFB=45°
∴∠B=∠DFB
∴DF=BD
∵CF=DF
∴BD=CF

3．证明：连结AF[来源:Z*xx*k.Cm]
∵EF是AB的垂直平分线
∴AF=BF
∴∠B=∠BAF
∴∠A=120°
∴∠B=∠BAF=30°
∴∠FAC=90°
∵AB=AC
∴∠C=∠B=30°
A
B
C
F
E
图（7）
∴AF= CF，即CF=2AF
∵AF=BF
∴CF=2B 4．证明：∵BE⊥AC，CF⊥AB
∴∠BEC=∠CFB=90°
在Rt△BCF和Rt△CBE中
BC=BC
CF=BE
∴Rt△BCF≌Rt△CBE（HL）
∴∠ABC=∠ACB
∴AB=AC