初中4.2 平行四边形授课课件ppt

这是一份初中4.2 平行四边形授课课件ppt，共10页。
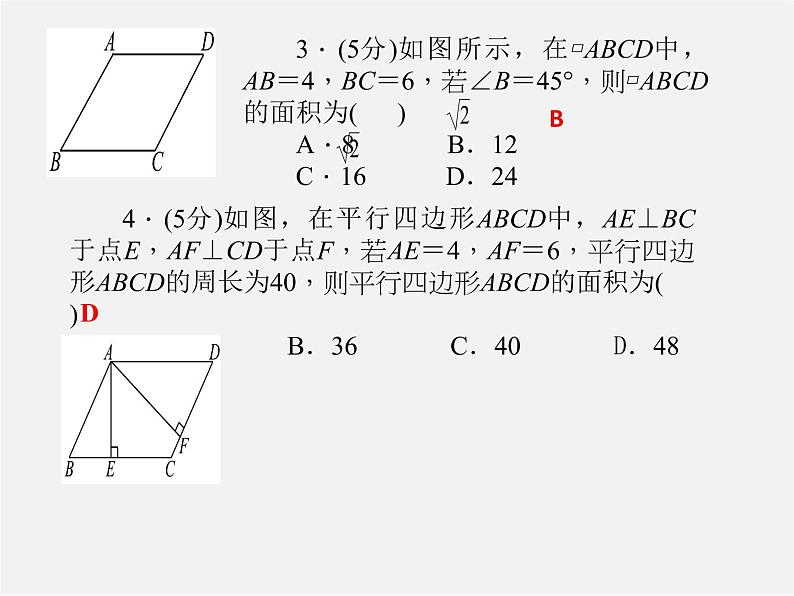
3．(5分)如图所示，在▱ABCD中，AB＝4，BC＝6，若∠B＝45°，则▱ABCD的面积为( )A．8 B．12C．16 D．24
4．(5分)如图，在平行四边形ABCD中，AE⊥BC于点E，AF⊥CD于点F，若AE＝4，AF＝6，平行四边形ABCD的周长为40，则平行四边形ABCD的面积为( )A．24　 　　B．36　　 　C．40　　　 D．48
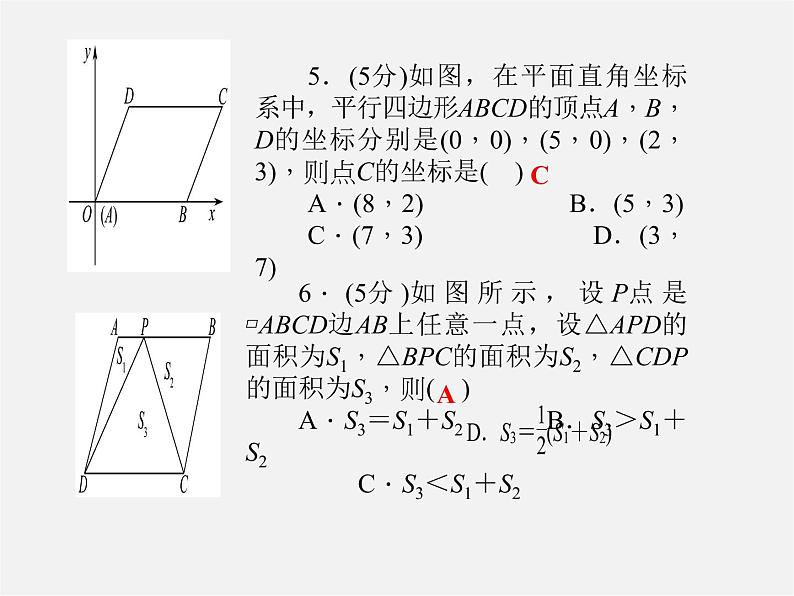
5．(5分)如图，在平面直角坐标系中，平行四边形ABCD的顶点A，B，D的坐标分别是(0，0)，(5，0)，(2，3)，则点C的坐标是( )A．(8，2) B．(5，3)C．(7，3) D．(3，7)
6．(5分)如图所示，设P点是▱ABCD边AB上任意一点，设△APD的面积为S1，△BPC的面积为S2，△CDP的面积为S3，则( )A．S3＝S1＋S2 B．S3＞S1＋S2 C．S3＜S1＋S2
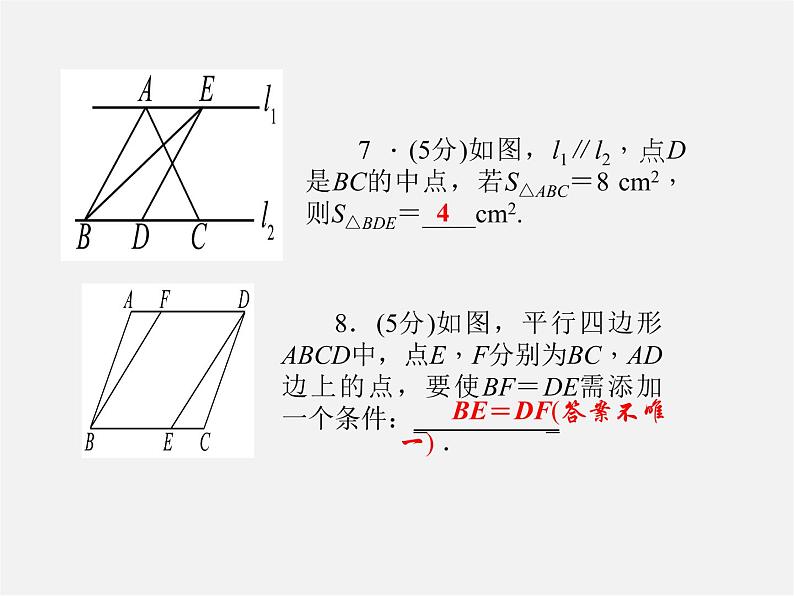
7 ．(5分)如图，l1∥l2，点D是BC的中点，若S△ABC＝8 cm2，则S△BDE＝____cm2.
8．(5分)如图，平行四边形ABCD中，点E，F分别为BC，AD边上的点，要使BF＝DE需添加一个条件：_ _
BE＝DF(答案不唯一) ．
9．(10分)已知：点E，F分别是平行四边形ABCD的对边AB，CD的中点，求证：DE＝FB.
证明：∵ABCD为平行四边形，∴AD＝BC，∠A＝∠C，AB＝DC，∵E，F分别为AB，CD的中点，∴AE＝CF，在△DAE与△BCF中，AD＝BC，∠A＝∠C，AE＝CF，∴△DAE≌△BCF(SAS)，∴DE＝BF. 
10．(6分)两个长、宽各为a米、b米的矩形花圃，都修建了形状不同的一条宽为c米的小路，问：这两条小路的面积____(填“相等”或“不相等”)，若相等，面积是____m2.
11．(10分)如图所示，四边形ABCD是平行四边形，点E在BA的延长线上，且BE＝AD，点F在AD上，AF＝AB.求证：△AEF≌△DFC.
证明：∵四边形ABCD是平行四边形∴AB＝CD，AB∥CD，∴∠D＝∠EAF，∵AF＝AB，BE＝AD，∴AF＝CD，AD－AF＝BE－AB，即DF＝AE，在△AEF和△DFC中，AE＝DF，
∠EAF＝∠D，AF＝DC，∴△AEF≌△DFC(SAS)
12．(10分)如图，在▱ABCD中，AE⊥BC，AF⊥CD，∠EAF＝60°，EC＝2，CF＝1.求▱ABCD的周长及∠B的度数．
解：∵∠EAF＝60°，∴∠C＝360°－∠AEC－∠AFC－∠EAF＝120°，∴∠B＝∠D＝180°－∠C＝60°设AB＝CD＝2x，则BE＝x，BC＝x＋2，
 13．(12分)如图所示，在形状为平行四边形的一块地ABCD中，有一条弯曲的小路EFG.现在想把它改为经过点E的直路，要求小路的两侧土地面积不变，请在图中画出改动后的小路，并说明理由．
解：连接EG，过点F作MN∥EG，交AD于点M，交BC于点N，连接EM，则EM就是所求的路．理由：因为MN∥GE，所以S△EGF＝S△EGM，所以S五边形ABEFG＝S四边形ABEG＋S△EGF＝S四边形ABEG＋S△EGM＝S四边形ABEM，即路左侧面积未变，则右侧面积也未变。
14．(12分)在平行四边形ABCD中，(1)当E点是AB上一点，F是CD上一点，且AE＝CF时，如图①所示，求证：AF＝CE，∠ECF＝∠EAF；(2)当E点变为BA延长线上一点，F变为DC延长线上一点，且AE＝CF时，如图②所示，问(1)中的结论是否仍成立？