浙教版八年级下册5.1 矩形课文内容课件ppt

这是一份浙教版八年级下册5.1 矩形课文内容课件ppt，共17页。PPT课件主要包含了矩形有哪些性质，温故知新，矩形的判定，∴ADDB，又∵CDDE，∵∠ACBRt∠，矩形的对角线相等，∴CEAB，∴∠ACB90°，还有其它证法吗等内容，欢迎下载使用。

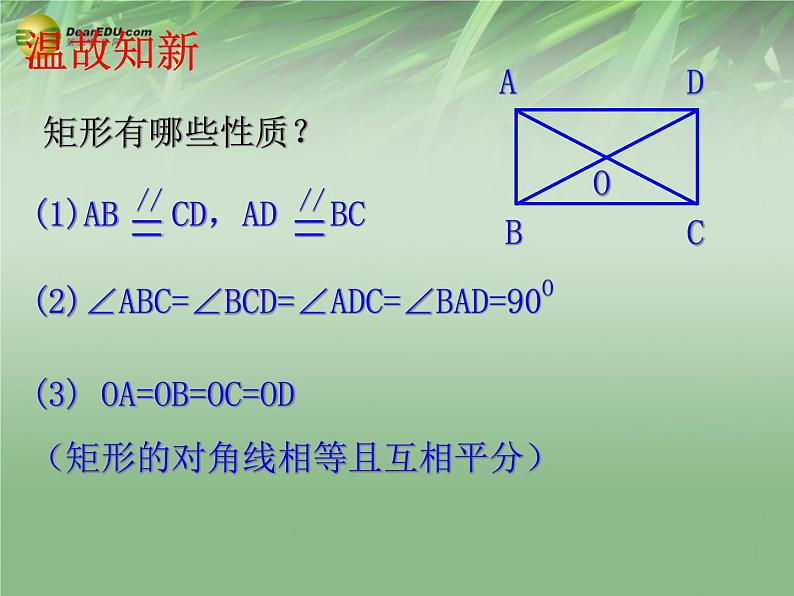
(2)∠ABC=∠BCD=∠ADC=∠BAD=90O
(3) OA=OB=OC=OD（矩形的对角线相等且互相平分）
定理1：有三个角是直角的四边形是矩形
定理2：对角线相等的平行四边形是矩形
有一个角是直角的平行四边形叫是矩形
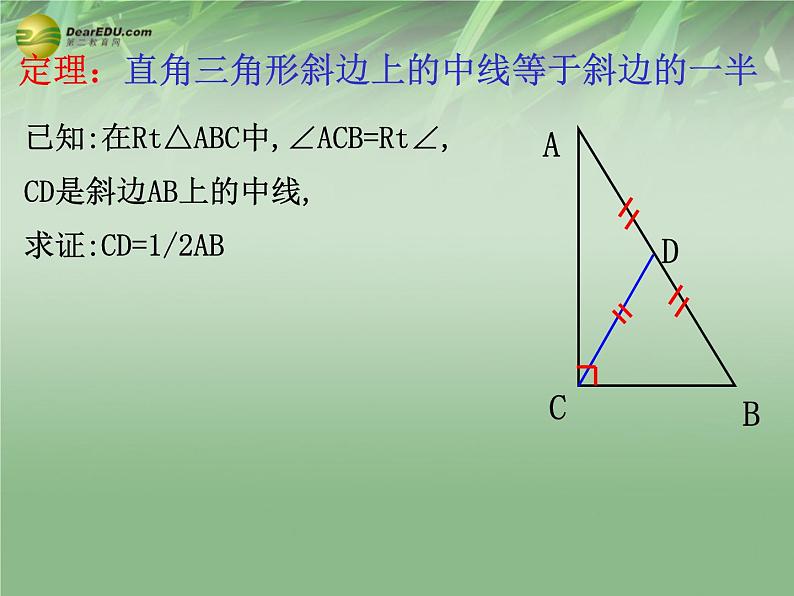
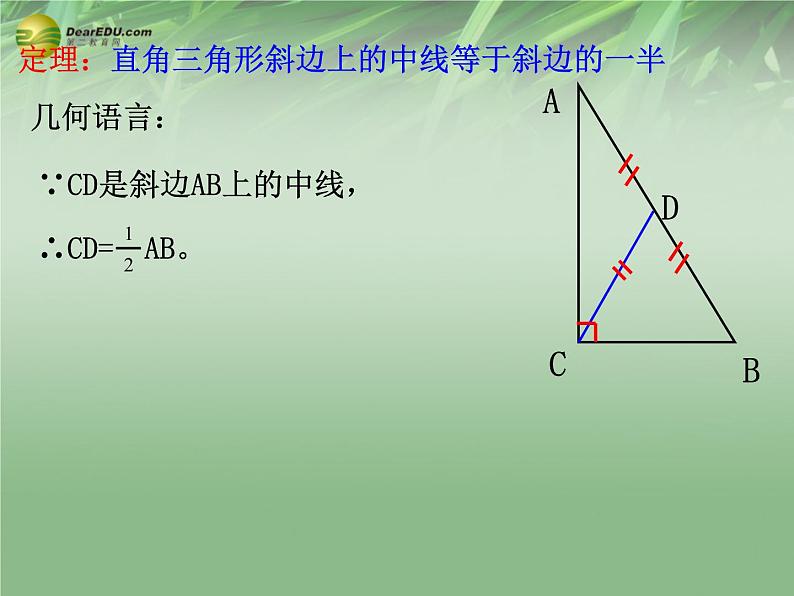
定理：直角三角形斜边上的中线等于斜边的一半
已知:在Rt△ABC中,∠ACB=Rt∠,CD是斜边AB上的中线,求证:CD=1/2AB
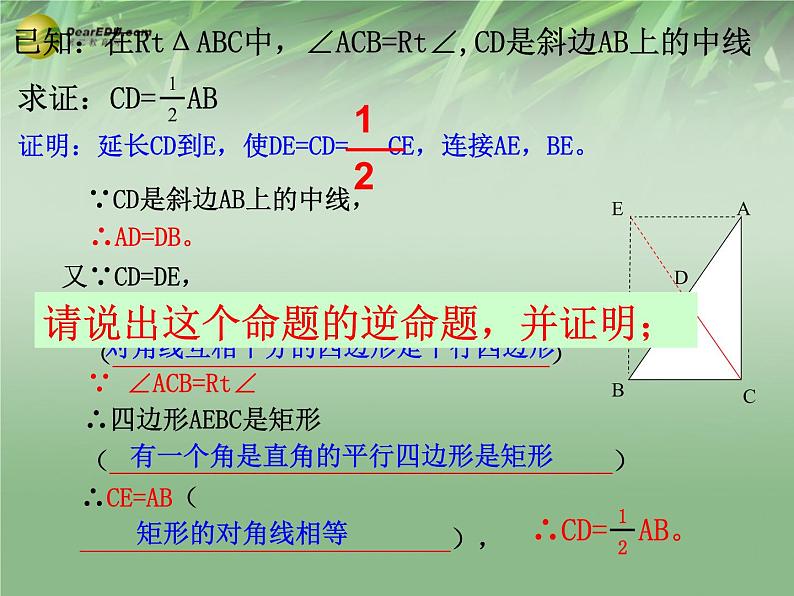
已知：在RtΔABC中，∠ACB=Rt∠,CD是斜边AB上的中线
证明：延长CD到E，使DE=CD= CE，连接AE，BE。
∵CD是斜边AB上的中线，
∴四边形AEBC是平行四边形（_________________________________）
∴CE=AB（____________________________），
∴四边形AEBC是矩形（______________________________________）
对角线互相平分的四边形是平行四边形
有一个角是直角的平行四边形是矩形
请说出这个命题的逆命题，并证明；
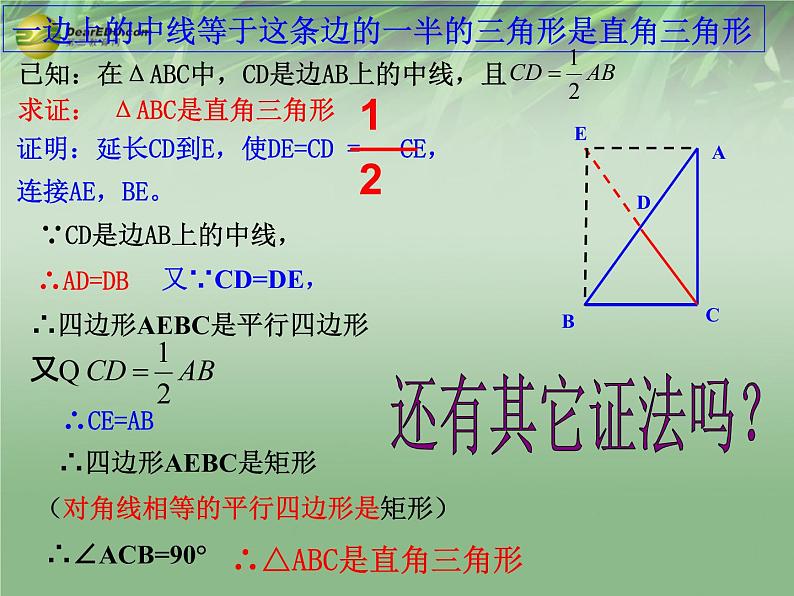
一边上的中线等于这条边的一半的三角形是直角三角形
求证： ΔABC是直角三角形
∵CD是边AB上的中线，
∴四边形AEBC是平行四边形
∴四边形AEBC是矩形
（对角线相等的平行四边形是矩形）
∴△ABC是直角三角形
1、证明一条线段是另一条线段的1/2或2倍，常用的定理：“三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半”
2、添辅助线的方法：延长短的使它等于原来的，再证相等；或在长的上截取一段使它等于短，再证中点。
（3）如图，在矩形ABCD中，E是BC的中点，∠BAE=30O，AE=2，则BD=________
（4）如图，在Rt△ABC中,中∠ACB=Rt∠,CD是斜边AB上的中线,已知∠DCA=250, ∠A= , ∠B= ;
（5）如图，已知BC=20m， ∠B=∠C=30°， E、G分别为AB，AC的中点，P为BC的中点，且EF⊥BC， GH⊥BC，垂足分别为F，H，求EF、PG的长；
（6）一张平行四边形纸片如图。现要求剪一刀，把它分成两部分，然后做适当的图形变换，把剪开的两部分拼成一个矩形，说明你的剪法和所采用的变换。
例、求证：在直角三角形中，300角所对直角边等于斜边的一半。
已知：在RtΔABC中，∠ACB=Rt∠, ∠A= 30°
在直角三角形中，等于斜边一半的直角边所对的角等于30°
已知：在RtΔABC中，∠ACB=Rt∠,
求证：∠A= 30°
3、在矩形ABCD中，E是BC上一点，已知AE=AD,DF垂直与AE于点F,求证：CE=FE
证明一条线段是另一条线段的1/2或2倍，（１）常用的定理：
（2）添辅助线的方法：
“三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半”
延长短的一倍，再证它与长的线段相等；或在长的上截取中点,再证中点取得的一半等于短的，