浙教版八年级下册2.3 一元二次方程的应用授课ppt课件

这是一份浙教版八年级下册2.3 一元二次方程的应用授课ppt课件，共16页。PPT课件主要包含了合作学习，做一做，谈谈这节课的学习体会等内容，欢迎下载使用。

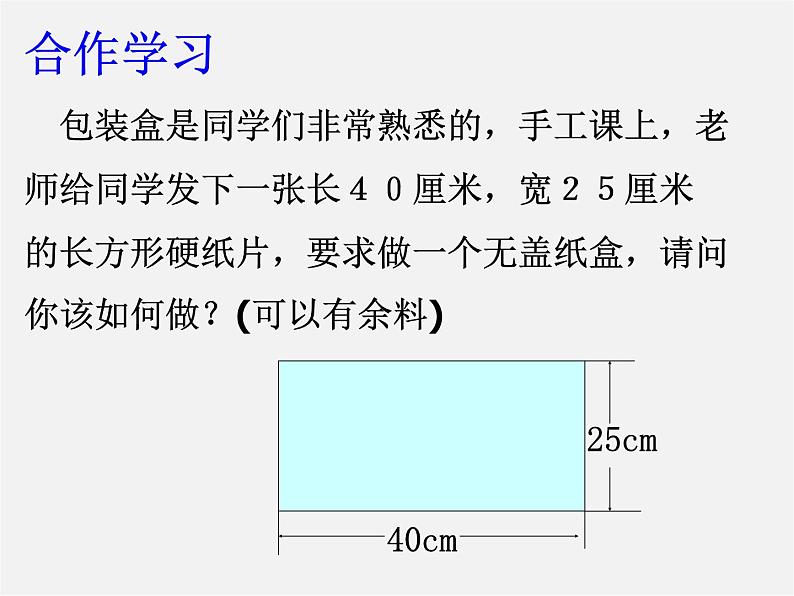
　包装盒是同学们非常熟悉的，手工课上，老师给同学发下一张长４０厘米，宽２５厘米的长方形硬纸片，要求做一个无盖纸盒，请问你该如何做？(可以有余料)
请问：１、同学做的纸盒大小都相同吗？
2、若确定小正方形边长为５厘米，你还能计算哪些量？
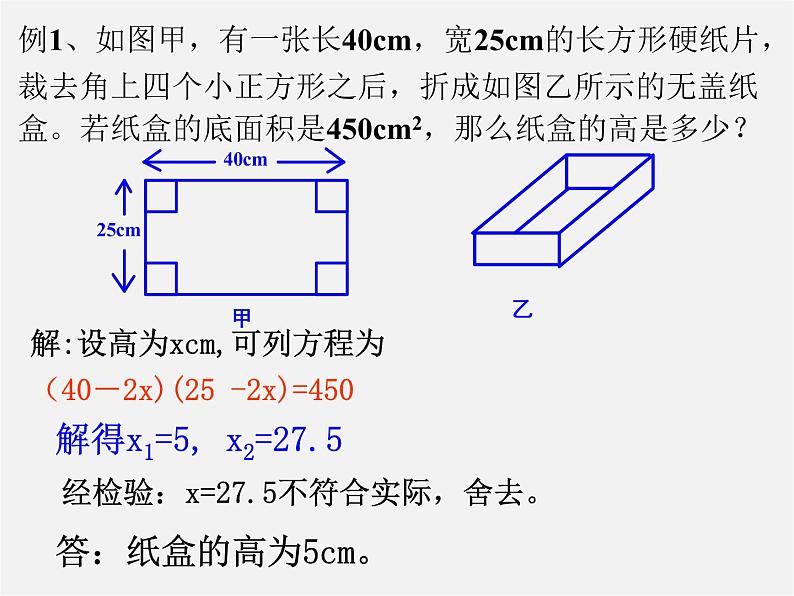
例1、如图甲，有一张长40cm，宽25cm的长方形硬纸片，裁去角上四个小正方形之后，折成如图乙所示的无盖纸盒。若纸盒的底面积是450cm2，那么纸盒的高是多少？
解:设高为xcm,可列方程为（40－2x)(25 -2x)=450
解得x1=5, x2=27.5
经检验：x=27.5不符合实际，舍去。
答：纸盒的高为5cm。
练一练：某中学为美化校园，准备在长32m，宽20m的长方形场地上，修筑若干条笔直等宽道路，余下部分作草坪，下面请同学们共同参与图纸设计，要求草坪面积为540m2求出设计方案中道路的宽分别为多少米？
1、若设计方案图纸为如图，草坪总面积540m2
分析：利用“图形经过平移”，它的面积大小不会改变的道理，把纵横两条路平移一下
2、设计方案图纸为如图，草坪总面积540m2
3、设计方案图纸为如图，草坪总面积540m2
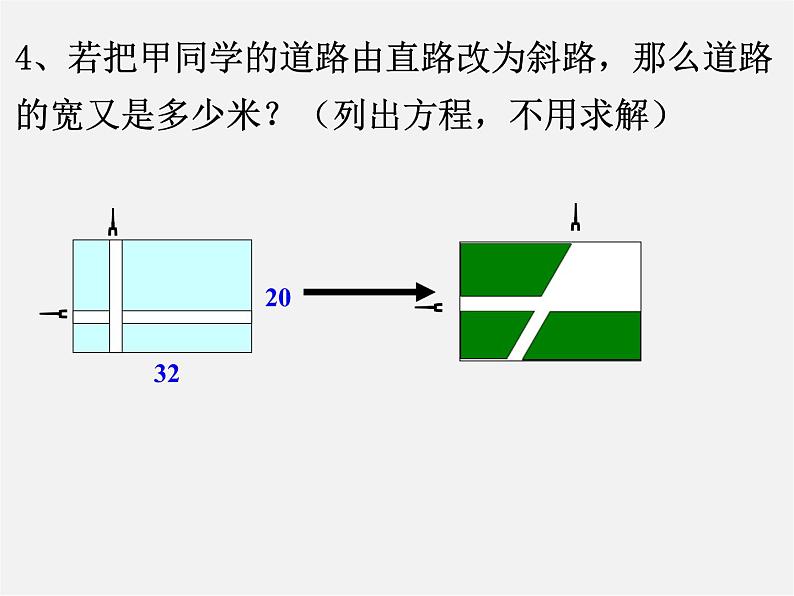
4、若把甲同学的道路由直路改为斜路，那么道路的宽又是多少米？（列出方程，不用求解）
一轮船以30km/h的速度由西向东航行在途中接到台风警报,台风中心正以20km/h的速度由南向北移动,已知距台风中心200km的区域(包括边界)都属于受台风影响区,当轮船接到台风警报时,测BC=500km,BA=300km.
(1)图中C表示什么?B表示什么?圆又表示什么?
(2)△ABC是什么三角形？能求出AC吗？
(3)显然当轮船接到台风警报时,没有受到台风影响，为什么？
(5)在这现象中存在哪些变量?
(4) 船是否受到台风影响与什么有关?
船的航向，速度以及台风的行进方向和速度
船、台风中心离A点的距离
(6)若设经过t小时后,轮船和台风中心位置分别在B1和C1的位置那么如何表示B1C1？
(7)当船与台风影响区接触时B1C1符合什么条件？
（8）船会不会进入台风影响区？如果你认为会进入，那么从接到警报开始，经过多少时间就进入影响区？　
B1C12=AC12+AB12
解:设当轮船接到台风警报后,经过t小时,则令：(400-30t)2+(300-20t)2=2002
问：(1) 这方程解得的t1,t2的实际意义是什么？
(2) 从t1,t2的值中，还可得到什么结论？
解得：t1≈8.35 t2≈19.34
(3) 如何才能避免轮船不进入台风影响区？
轮船首次受到台风影响的时间和最后受到影响的时间
假如轮船一直不改变航向或速度，从开始到结束影响的总时间
（4）如果船速为10 km/h,结果将怎样?
解:设当轮船接到台风警报后,经过t小时,则令：(400-10t)2+(300-20t)2=2002
化简，得：t2-40t+420=0
∴轮船继续航行不会受到台风的影响。
如图，在△ABC中，∠B=90。点P从点A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别从A，B同时出发，经过几秒， △ PBQ的面积等于8cm2 ？
∴（6-x）×2x÷2=8
∵ S△PBQ=BP×BQ÷2
BP=6-x，BQ=2x
解得：x1=2，x2=4