初中数学浙教版八年级下册5.2 菱形教课内容ppt课件

这是一份初中数学浙教版八年级下册5.2 菱形教课内容ppt课件，共26页。PPT课件主要包含了定义法，课前热身，合作学习，且ABAD，菱形的判定，∴□ABCD是菱形，一组邻边相等，对角线互相垂直，四条边相等，菱形的判定方法等内容，欢迎下载使用。

（1）菱形的定义是什么？
（2）菱形有哪些性质？
（3）判定一个四边形是不是菱形可根据什么？
（4）菱形还有其他判定方法吗？
一组邻边相等的平行四边形叫做菱形
1.具有平行四边形的一切性质。
2.菱形本身具有的特殊性质:四条边相等, 两条对角线互相垂直平分, 每一条对角线平分一组对角.
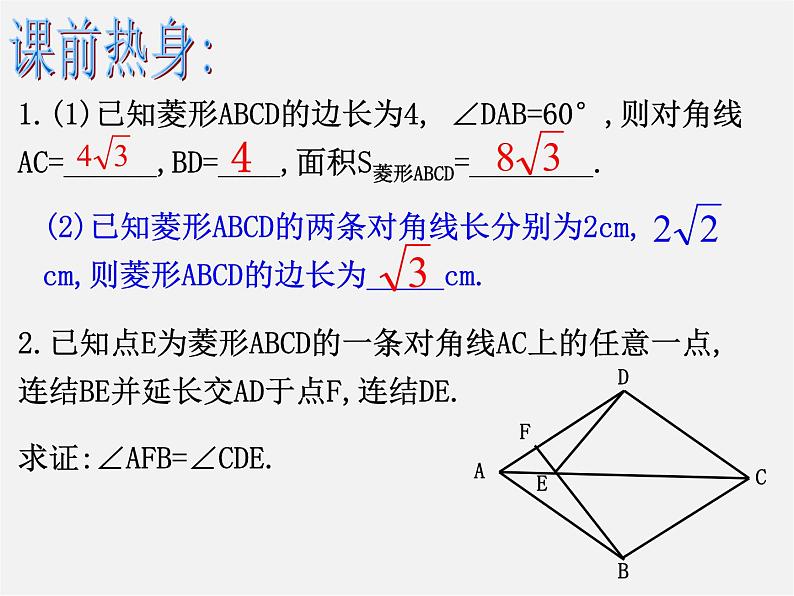
1.(1)已知菱形ABCD的边长为4, ∠DAB=60°,则对角线AC=______,BD=____,面积S菱形ABCD=________.
2.已知点E为菱形ABCD的一条对角线AC上的任意一点,连结BE并延长交AD于点F,连结DE.求证:∠AFB=∠CDE.
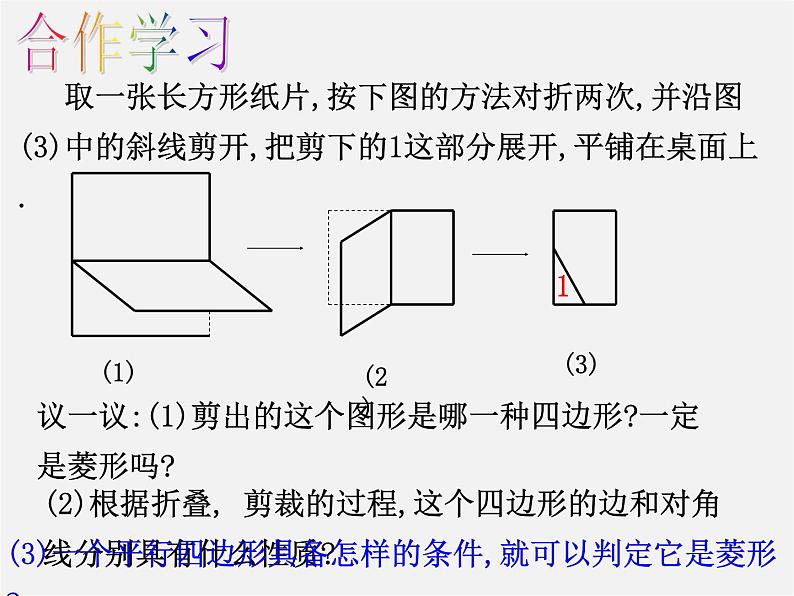
取一张长方形纸片,按下图的方法对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.
议一议:(1)剪出的这个图形是哪一种四边形?一定是菱形吗?
(2)根据折叠, 剪裁的过程,这个四边形的边和对角线分别具有什么性质?
(3)一个平行四边形具备怎样的条件,就可以判定它是菱形?
根据菱形的定义,可得菱形的判定方法1：
有一组邻边相等的平行四边形叫做菱形.
∵四边形ABCD是平行四边形，
∴四边形ABCD是菱形.
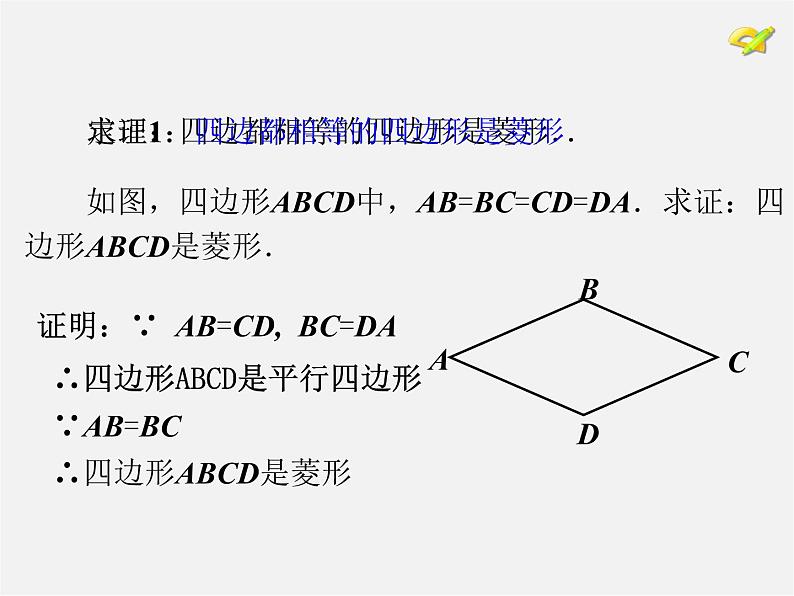
　　求证：四边都相等的四边形是菱形．　　　
　　如图，四边形ABCD中，AB=BC=CD=DA．求证：四边形ABCD是菱形．
　　定理1：四边都相等的四边形是菱形．
证明：∵ AB=CD, BC=DA ∴四边形ABCD是平行四边形 ∵AB=BC ∴四边形ABCD是菱形
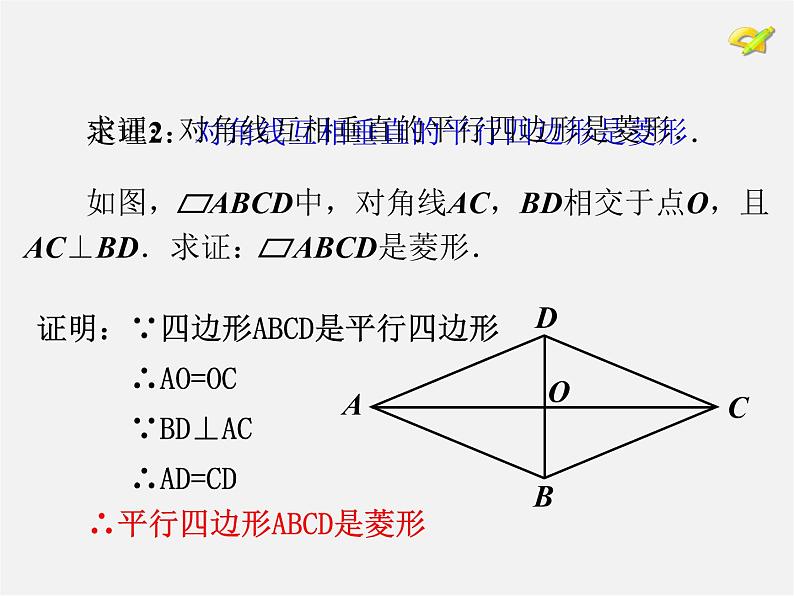
　　定理2：对角线互相垂直的平行四边形是菱形．
　　求证：对角线互相垂直的平行四边形是菱形．　　　
证明：∵四边形ABCD是平行四边形 ∴AO=OC ∵BD⊥AC ∴AD=CD
∴平行四边形ABCD是菱形
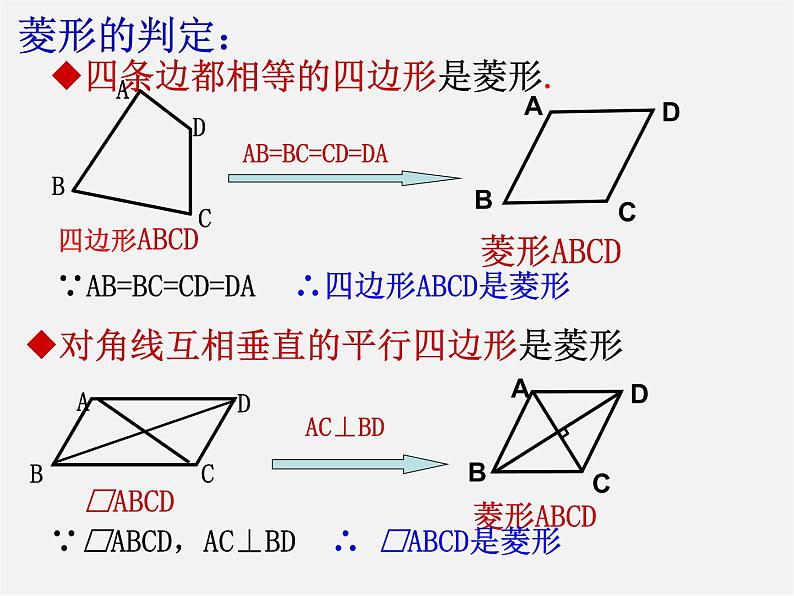
四条边都相等的四边形是菱形.
∵AB=BC=CD=DA
∴四边形ABCD是菱形
对角线互相垂直的平行四边形是菱形
∵□ABCD，AC⊥BD
1、画一个菱形，使它的两条对角线的长分别为4cm和6cm。
（1）两条对角线互相垂直的四边形是菱形. ( )
（2）两条对角线互相垂直平分的四边形是菱形. ( )
例1、如图，在 矩形ABCD中，对角线AC垂直平分与AD，BC分别交于E，F 求证：四边形AFCE是菱形
证明:∵四边形ABCD是矩形, ∴AE//FC(矩形的定义) ∴∠EAC=∠ACF 又∵∠AOE=∠COF,AO=CO, ∴△AOE≌△COF, ∴EO=FO. ∴四边形是平行四边形 (对角线相互平分的四边形是平行四边形). ∵EF⊥AC ∴四边形AFCE是菱形 (对角线互相垂直的平行四边形是菱形).
（2）∵ 四边形ABCD是平行四边形， ∵AC⊥BD ∴四边形ABCD是菱形.
（2）四边形ABCD是菱形吗？为什么？
1.已知，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F。 求证：四边形AEDF是菱形。
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形
∴平行四边形AEDF是菱形.
∴∠ADE=∠DAF.
∵AD是△ABC的角平分线,
∴∠DAE=∠DAF.
∴∠DAE=∠ADE.
2、一边长为5cm平行四边形的两条对角线的长分别为6cm和8cm，求证：这个平行四边形为菱形。
3、如图，在等边三角形ABC中，D，E，F分别是各边的中点。连结DE、EF、FD图中有菱形吗？如果有，请你把它们找出来。
4、已知如图，在四边形ABCD中，E，F，G，H依次是AB、BC、CD、DA的中点，请添一个条件，使四边形DFGH为菱形。
解：添加的条件是： 理由是：
2.已知:如图,在四边形ABCD中,AC＝BD .E,F,G,H依次是AB,  BC,CD,DA的中点.求证:四边形EFGH是菱形.
∵E,F分别是AB,BC的中点,  ∴EF是△ABC的中位线,  ∴EF＝ AC(三角形的中位线等于第三边的一半).  同理,FG＝ BD,HG＝ AC,HE＝  BD  又∵AC＝BD,  ∴EF＝FG＝FG＝GH＝HE.  ∴四边形EFGH是菱形(四条边相等的四边形是菱形).
例2、求证：有一条对角线平分一个内角的平行四边形是菱形
已知：四边形ABCD是平行四边形，对角线AC平分∠DAB
求证：四边形ABCD是菱形
∵ 四边形ABCD是平行四边形
（两直线平行，内错角相等）
（在一个三角形中，等角对等边）
∴ 四边形ABCD是菱形
（邻边相等的平行四边形是菱形）
2、如图，在平行四边形ABCD中，∠BAD的平分线与BC交于点E，∠ABC的平分线与AD交于点F，AE与BF相交于点O。求证：四边形ABEF是菱形
3、将菱形ABCD沿AC方向平移至A1B1C1D1, A1D1交CD于点E, A1B1交BC于点F. 判断四边形A1FCE是不是菱形,并说明理由.
4、在直角坐标系中,点A,B,C,D的坐标依次为(-1,0), (x,y),(-1,5),(w,z).要使四边形ABCD为菱形,x,y,w,z的值必须满足什么条件?
3.如图，两张等宽的纸条交叉重叠在一起，猜想重叠部分的四边形ABCD是什么形状？说说你的理由。
全课小结——菱形的判定
四边相等的四边形是菱形
一组邻边相等的平行四边形是菱形
DE,EF是△ABC的两条中位线,我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的形状有什么关系.建议按下列步骤探索:(1)围成的四边形是否必定是平行四边形?
(2)在什么条件下,围成的四边形是菱形?
(3)在什么条件下,围成的四边形是矩形?
(4)你还能发现其他什么结论吗?
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,四边形AEFG是菱形吗?