浙教版九年级下册1.1 锐角三角函数说课课件ppt

这是一份浙教版九年级下册1.1 锐角三角函数说课课件ppt，共25页。PPT课件主要包含了探索园地，初识三角函数，相信自己能行﹗，第一章解直角三角形，登高望远，三角函数的由来等内容，欢迎下载使用。
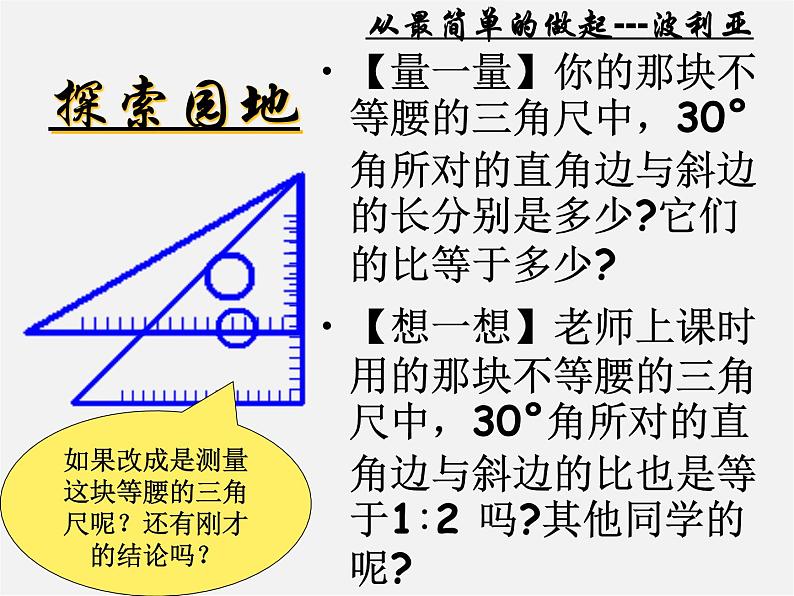
从最简单的做起---波利亚
【量一量】你的那块不等腰的三角尺中，30°角所对的直角边与斜边的长分别是多少?它们的比等于多少?【想一想】老师上课时用的那块不等腰的三角尺中，30°角所对的直角边与斜边的比也是等于1∶2 吗?其他同学的呢?
如果改成是测量这块等腰的三角尺呢？还有刚才的结论吗？
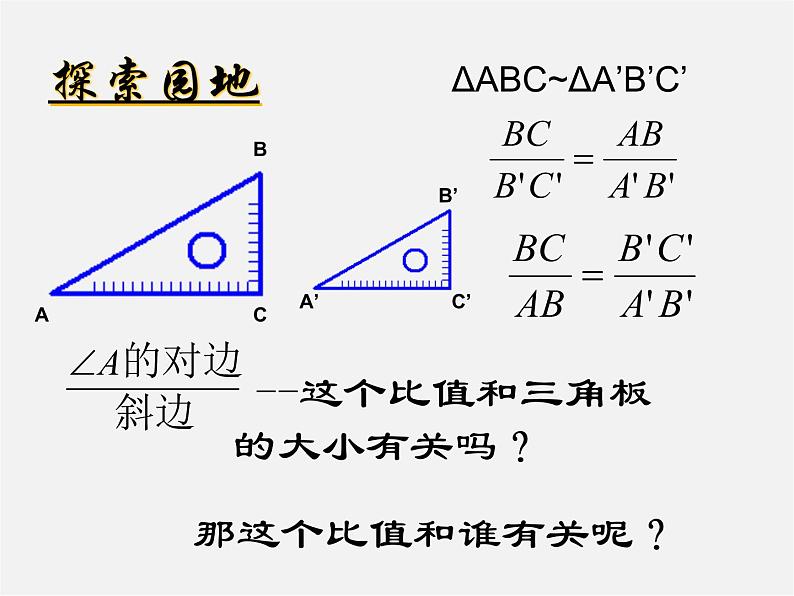
--这个比值和三角板的大小有关吗？
ΔABC~ΔA’B’C’
那这个比值和谁有关呢？
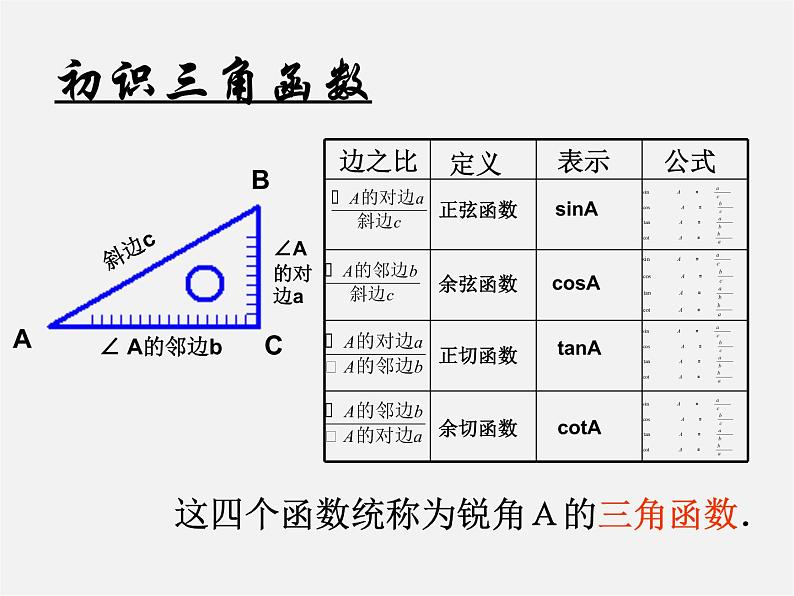
这四个函数统称为锐角Ａ的三角函数．
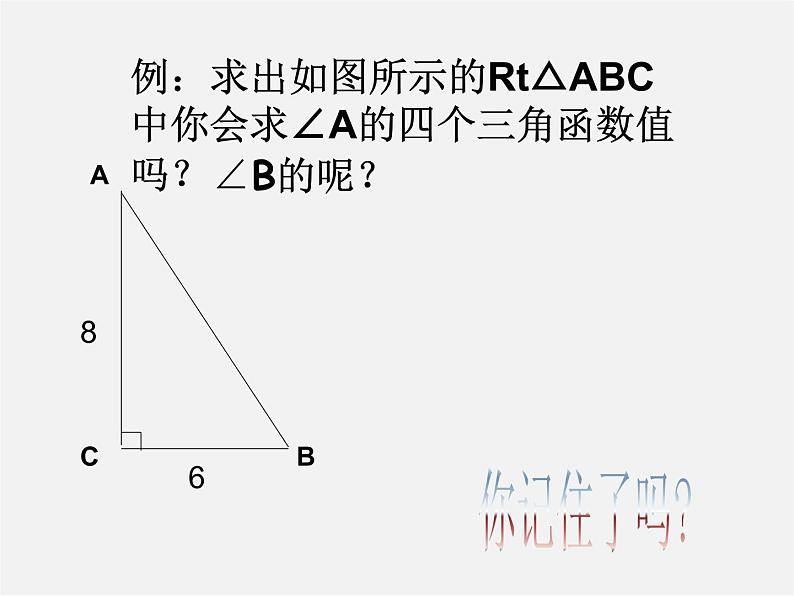
例：求出如图所示的Rt△ABC中你会求∠A的四个三角函数值吗？
２、如图所示的长方形分割成四个大小相同的正方形。已知正方形的边长为a,则tan = ____ , sin =______
１、如图所示：则sin =_____， cs = ______， tan = _____，ct =_______。
３、等腰三角形的腰长为5cm,底边长为8cm，则它的底角的正切值是____．
4、已知sinA= ,求csA,tanA,ctA的值．
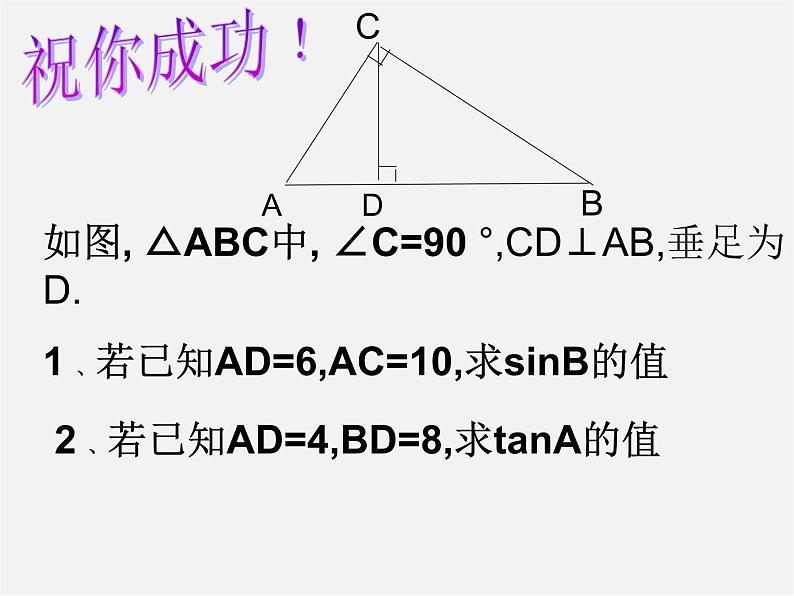
2 、若已知AD=4,BD=8,求tanA的值
如图, △ABC中, ∠C=90 °,CD⊥AB,垂足为D.1 、若已知AD=6,AC=10,求sinB的值
根据三角函数定义，你能确定锐角A的正弦与余弦三角函数值 的取值范围吗？
并找一找∠A的四个三角函数之间有何关系？
小结：1、这节课我们学了什么？2、今后在涉及直角三角形的 边角关系时，你会选择什么方法去解决？
作业：1、第109页练习2、3，第111页习题19.3第一题 2、你能用所学知识分别求出30 ° 、45°、 60 °的三角 函数 值吗？
思考题：1、若y=sinA+3,则y取值范围为________2、如图，在Rt Δ ABC中， ∠B=90 °，则sinA =____ csA =______,猜想： sin²A+ cs²A=_____
如图,小红骑车上学路上要依次经过这样的三个斜坡,你认为哪一个斜坡更陡些?并说一说你是用什么方法来判别的?
1.1 锐角三角函数 2
第一章 解直角三角形
1.1 锐角三角函数
分别在倾斜角为30°和40°的斜坡上步行了150米,则乙队比甲队高多少米?
在两个倾斜角不同的斜坡上都步行了150米，请问哪个队登得高?
思考：在上述过程中，哪些量是保持不变的？
在直角三角形中,当∠A=30 °时,
与点B在角的边上的位置无关.
　　三角测量在我国出现的很早．据记载，早在公元前两千年，大禹就利用三角形的边角关系，来进行对山川地势的测量．
　　“三角学”一词，是由希腊文三角形与测量二字构成的，原意是三角形的测量，也就是解三角形．后来范围逐渐扩大，成为研究三角函数及其应用的一个数学分支．
１、如图，在Rt△ABC中，∠C=Rt∠,若AB=5，BC=3.
(2)请求出∠B的正弦、余弦和正切的值.
(1)求∠A的正弦、余弦和正切的值；
(3)观察(1)(2)中的计算结果,你发现了什么?
当∠A+∠B=90°时,
tanA·tanB=1.
问题：甲、乙两队分别在倾斜角为30°和40°的斜坡上都步行了150米，那么乙队比甲队高多少米？
拓展问题1：如图，已知甲队步行了600米到达山顶C处，请问乙队要步行多少米才能到达山顶？
拓展问题2：利用图中的数据，若测得∠PAD的度数，我就能求出塔高PC，你能说出其中的道理吗？
经历了一个探究过程：特殊到一般
学习了一个重要概念：锐角三角函数
体现了一种数学思想：数形结合