数学九年级上册4.5 相似三角形的性质及应用示范课ppt课件

这是一份数学九年级上册4.5 相似三角形的性质及应用示范课ppt课件，共24页。PPT课件主要包含了怎样测量河宽，初步尝试，答楼高36米，一起来试一试，当堂巩固，基础演练，挑战自我，自我挑战，课外拓展，课堂小结等内容，欢迎下载使用。
1．三角形中的“三线”与相似比相似三角形对应高的比、对应中线的比与对应角平分线的
比、都________相似比．
2．周长与相似比(1)相似三角形周长的比________相似比．
(2)相似多边形周长的比________相似比．
3．面积比与相似比(1)相似三角形面积的比等于相似比的________．
(2)相似多边形面积的比等于相似比的________．
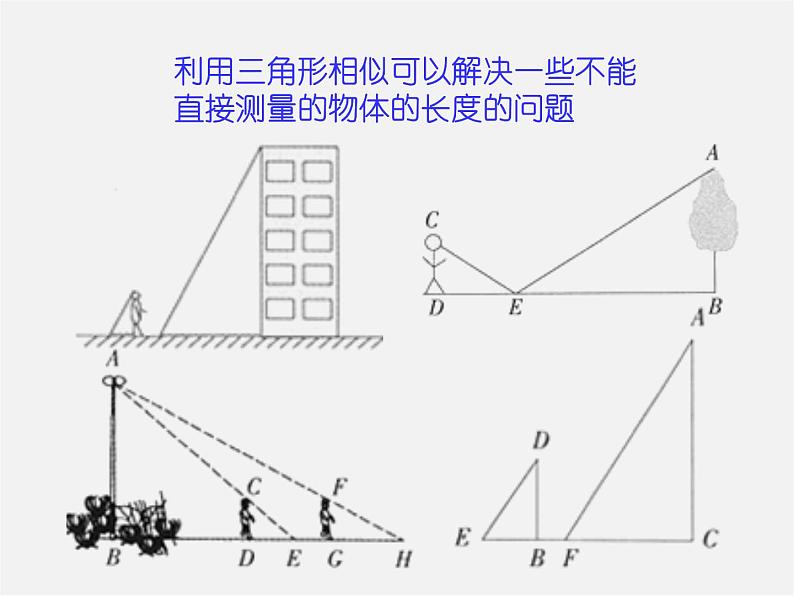
世界上最高的楼——台北101大楼
怎样测量这些非常高大物体的高度？
世界上最宽的河——亚马孙河
利用三角形相似可以解决一些不能直接测量的物体的长度的问题
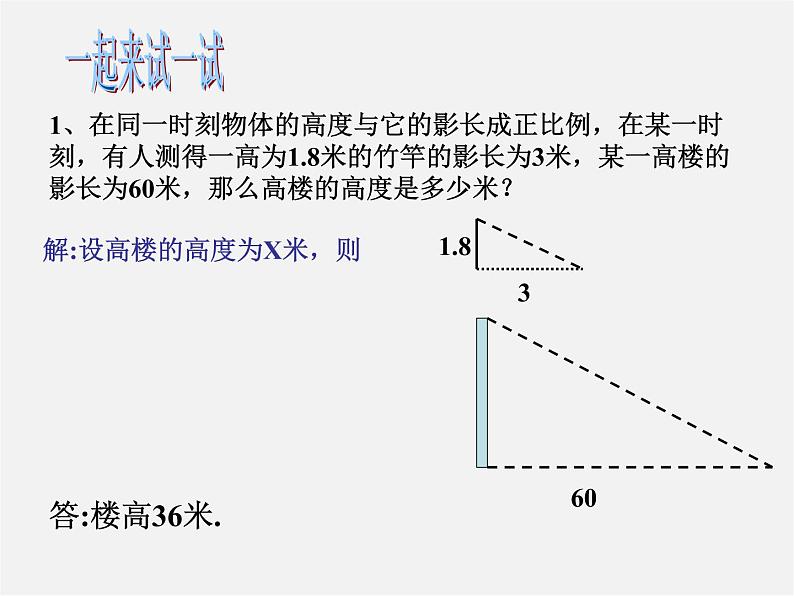
1、在同一时刻物体的高度与它的影长成正比例，在某一时刻，有人测得一高为1.8米的竹竿的影长为3米，某一高楼的影长为60米，那么高楼的高度是多少米？
解:设高楼的高度为X米，则
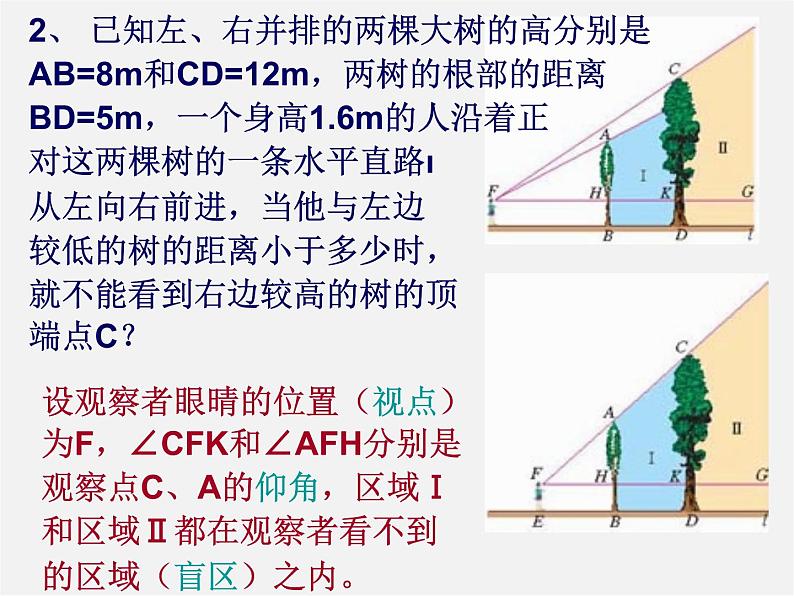
2、 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m，两树的根部的距离BD=5m，一个身高1.6m的人沿着正对这两棵树的一条水平直路ι从左向右前进，当他与左边较低的树的距离小于多少时，就不能看到右边较高的树的顶端点C？
设观察者眼晴的位置（视点）为F，∠CFK和∠AFH分别是观察点C、A的仰角，区域Ⅰ和区域Ⅱ都在观察者看不到的区域（盲区）之内。
解：假设观察者从左向右走到点E时，他的眼睛的位置点F与两棵树的顶端点A、C在一条直线上。 ∵AB⊥ι，CD⊥ι ， ∴AB∥CD，△AFH∽△CFK， ∴FH：FK=AH：CK，即 ，解得FH=8.
当他与左边较低的树的距离小于8m时，就不能看到右边较高的树的顶端点C。
例3 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m，两树的根部的距离BD=5m，一个身高1.6m的人沿着正对这两棵树的一条水平直路ι从左向右前进，当他与左边较低的树的距离小于多少时，就不能看到右边较高的树的顶端点C？
方法一：利用阳光下的影子。
小雨把长为2.4米的标杆CD直立在地面上， 量出树影长2.8米，标杆影长1.47米
（太阳光线可以近似的看作平行线）
小商在树前面的地面上平放一面镜子（E），观测者沿着直线BE后退到点D，调整位置使恰好在镜子里看到树梢顶点A.测量出：BE=8m DE=2.8m CD=1.6m
方法二：利用镜子的反射。（入射角等于反射角）
方法三：利用标杆小明在地面直上立一根标杆EF，沿着直线BF后退到点D，使眼睛C、标杆的顶点E 、树梢的顶点A在同一直线上。
测量：人与标杆的距离DF， 人与树的距离DB 人的目高和标杆的高度
方法四：利用标尺用手举一根标尺EF，让标尺与地面垂直，调整人与树的距离或眼睛与标尺的距离，使标尺刚好挡住树的高度。
测量：人与标尺的距离，人与树的距离 确认标尺的长度
依据：相似三角形对应高的比等于相似比。
步枪在瞄准时的示意图如图，从眼睛到准星的距离OE为80cm，步枪上准星宽度AB为2mm，目标的正面宽度CD为50cm，求眼睛到目标的距离OF。
解：由题意得，△OAB∽ △OCD，
解得：OF=20000（cm） =200(m).
如图，△ABC是一块锐角三角形余料，边BC=120毫米，高AD=80毫米，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？
解：设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。因为PN∥BC，所以△APN∽ △ABC所以
在Rt△ ABC中，∠C=90。，AC=4，BC=3，
（3）如图3，三角形内有并排的三个相等的正方形，它们组成的矩形内接于△ ABC，求正方形的边长。
（2）如图2，三角形内有并排的两个相等的正方形，它们组成的矩形内接于△ ABC，求正方形的边长
（1）如图1，四边形DEFG为△ ABC的内接正方形，求正方形的边长。
（4）如图4，三角形内有并排的个正方形，它们组成的矩形内节于△ ABC，请写出正方形的边长。
1 相似三角形可应用于生活中的很多方面，主要是：测高（不能直接使用皮尺或刻度尺量的）测距（不能直接测量的两点的距离）
2 解决这类实际问题时：一般有以下步骤 ①审题 ②构建相似三角形 ③应用相似三角形列出比例式（方程） ④求出未知量