数学九年级下册2.3 三角形的内切圆教学演示课件ppt

这是一份数学九年级下册2.3 三角形的内切圆教学演示课件ppt，共30页。PPT课件主要包含了O就是所求的圆，巩固练习，a+b-c，三边的距离相等，想一想，比一比看谁做得快，腰长和中位线长相等，开动脑筋，学生归纳小结等内容，欢迎下载使用。
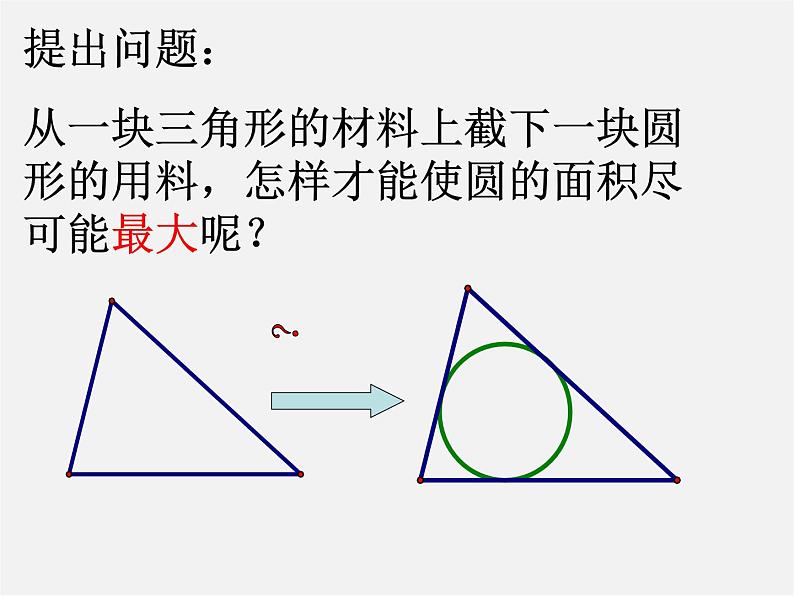
提出问题：从一块三角形的材料上截下一块圆形的用料，怎样才能使圆的面积尽可能最大呢？
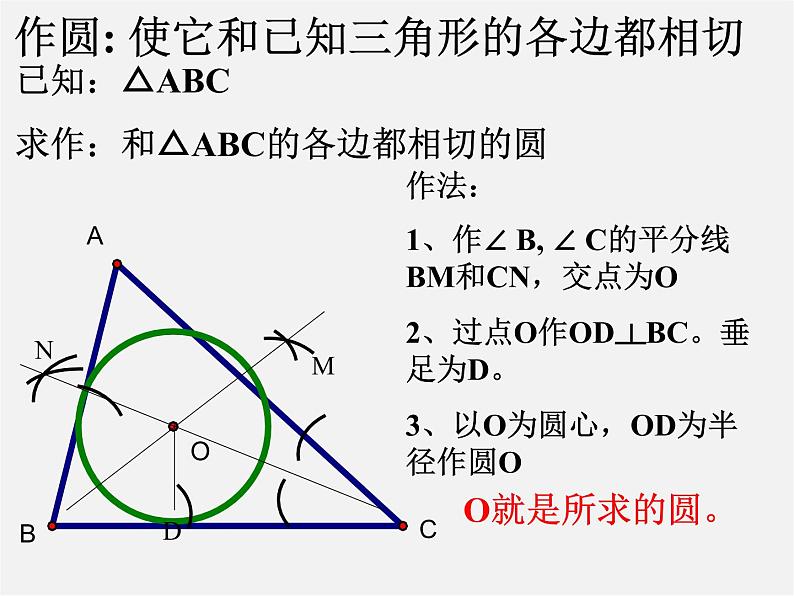
作圆: 使它和已知三角形的各边都相切
已知：△ABC求作：和△ABC的各边都相切的圆
2、和多边形的各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形。
概念；1、和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。
想一想：根据作法,和三角形各边都 相切的圆能作出几个？
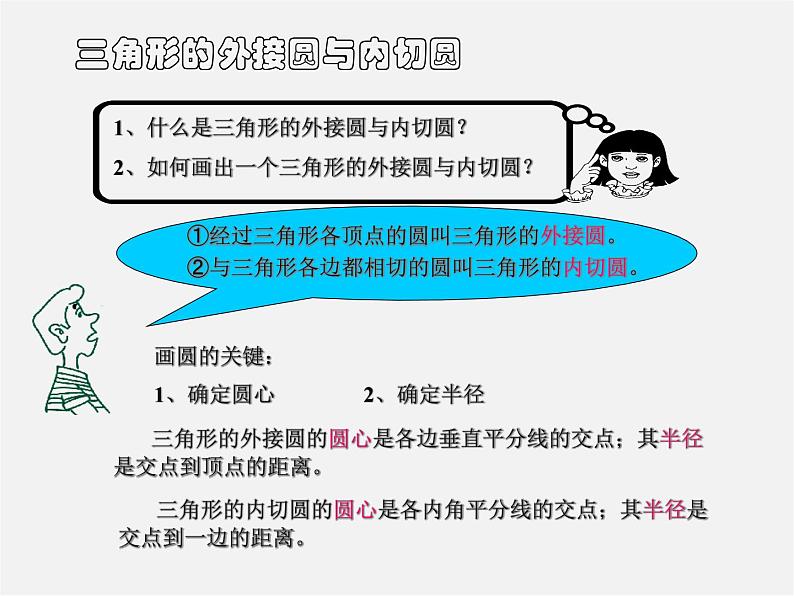
1、什么是三角形的外接圆与内切圆？2、如何画出一个三角形的外接圆与内切圆？
画圆的关键：1、确定圆心 2、确定半径
三角形的外接圆的圆心是各边垂直平分线的交点；其半径是交点到顶点的距离。
三角形的内切圆的圆心是各内角平分线的交点；其半径是交点到一边的距离。
三角形的外接圆与内切圆
①经过三角形各顶点的圆叫三角形的外接圆。　②与三角形各边都相切的圆叫三角形的内切圆。
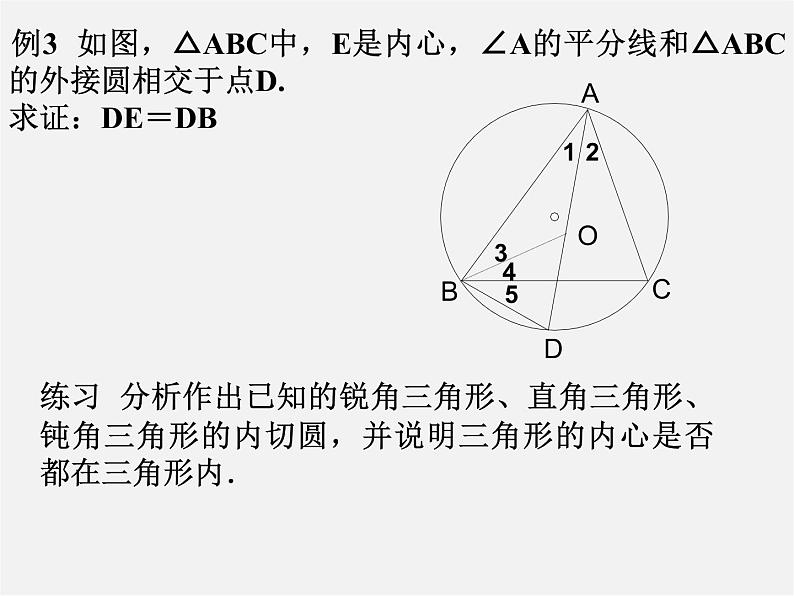
例3 如图，△ABC中，E是内心，∠A的平分线和△ABC的外接圆相交于点D.求证：DE＝DB
练习 分析作出已知的锐角三角形、直角三角形、钝角三角形的内切圆，并说明三角形的内心是否都在三角形内．
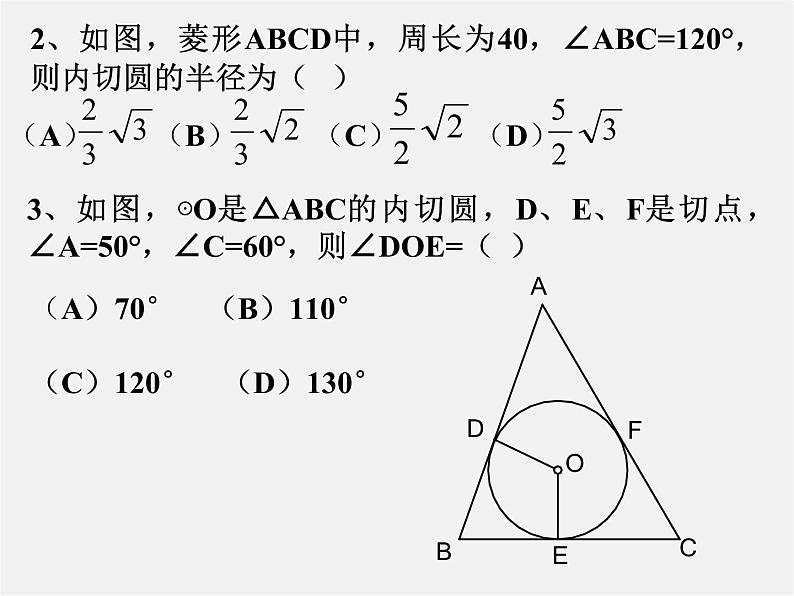
2、如图，菱形ABCD中，周长为40，∠ABC=120°，则内切圆的半径为（ ）
3、如图，⊙O是△ABC的内切圆，D、E、F是切点，∠A=50°，∠C=60°，则∠DOE=（ ）
（A）70° （B）110° （C）120° （D）130°
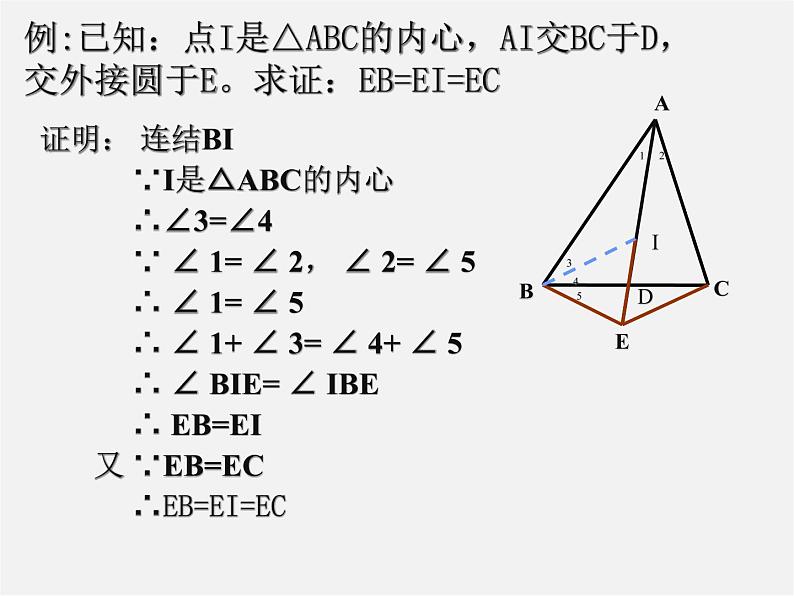
例:已知：点I是△ABC的内心，AI交BC于D，交外接圆于E。求证：EB=EI=EC
证明： 连结BI ∵I是△ABC的内心 ∴∠3=∠4 ∵ ∠ 1= ∠ 2， ∠ 2= ∠ 5 ∴ ∠ 1= ∠ 5 ∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5 ∴ ∠ BIE= ∠ IBE ∴ EB=EI 又 ∵EB=EC ∴EB=EI=EC
达标检测一、判断。1、三角形的外心到三角形各边的距离相等。 （ ）2、直角三角形的外心是斜边的中点。 （ ）二、填空：1、直角三角形的两条直角边分别是5cm和12cm，则它的外接圆 半径————，内切圆半径————。2、等边三角形外接圆半径与内切圆半径之比————。三、选择题：下列命题正确的是（ ）A、三角形外心到三边距离相等B、三角形的内心不一定在三角形的内部C、等边三角形的内心、外心重合D、三角形一定有一个外切圆
4、等边三角形的内切圆半径、外接圆的半径和高的比为（ ）
5、存在内切圆和外接圆的四边形一定是（ ）
（A）矩形（B）菱形 （C）正方形 （D）平行四边形
1、如图，△ABC中，∠A=55度，I是内心 则，∠BIC＝————度。
2、如图，△ABC中，∠A=55度，其内切圆切△ABC 于D、E、F，则∠FDE＝————度。
三、特殊三角形外接圆、内切圆半径的求法：
直角三角形外接圆、内切圆半径的求法
例：已知：点I是△ABC的内心，AI交BC于D，交外接圆于E。求证：EB=EI=EC
课堂练习：1、判断（1）三角形的外心是三边中垂线的交点。（ ）（2）三角形三边中线的交点是三角形内心。（ ）（3）若O为△ABC的内心， 则OA＝OB＝OC。（ ）
三个内角的角平分线的交点
提示：关键是利用内心的性质
如果∠ A＝120 ° ，∠ BOC=？
如果∠ A=n ° ， ∠ BOC=?
例1、如图，在△ABC中， ∠A=55 ° ，点O是外心，求∠ BOC的度数。
如果∠ A＝120 °呢？
例2、如图：点I是△ABC的内心，AI交边BC于点D，交△ABC外接圆于点E.求证：BE＝IE
提示：欲证BE＝IE 需证∠ BIE＝ ∠ IBE把∠ BIE转化为两圆周角之和
若已知圆的三条切线呢？
设△ABC的BC=a，CA=b，AB=c，内切圆I和BC、AC、AB分别相切于点D、E、F
y+z=ax+z=bx+y=c
分析：设 AF=x，BD=y，CE=z
圆的外切四边形具有什么性质？
圆的外切四边形的两组对边的和相等。
例：等腰梯形各边都与⊙O相切， ⊙O的直径为6cm，等腰梯形的腰等于8cm，则梯形的面积为_____。
若已知圆的四条切线呢？
如图：四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P。
根据已知条件可以得出什么结论？
例：已知在△ABC中，BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、 AB切于点D、E、F，求AF、BD和CE的长。
已知：在△ABC中，BC=14，AC=9，AB=13，它的内切圆分别和BC、AC、AB切于点D、E、F，求AF、BD和CE的长。
（2）如图，Δ ABC的内切圆分别和BC，AC，AB切于D，E，F；如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB=
（3）如图，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8CM，则Δ PDE的周长为（ ）
例：直角三角形的两直角边分别是5cm， 12cm 则其内切圆的半径为______。
圆的外切等腰梯形有什么特点？
圆的外切平行四边形有什么特点？
圆的外切平行四边形是菱形
课堂练习：练习册69 2 （1）（2）
1、三角形内切圆的作法2、三角形的内切圆，内心，圆外切三角形的概念。3、利用三角形的内心的性质证解有关问题。
课后作业： 书102－102 10、11、12 B组题 3
练习2 已知：△ABC是⊙O外切三形，切点为D，E，F。若BC＝14 cm ，AC＝9cm，AB＝13cm。求AF，BD，CE。
x+y=13y+z=14x+z=9
圆的外切四边形的两组对边和相等。
已知：四边形ABCD的边 AB，BC，CD，DA和圆O分别相切于L，M，N，P。探索圆外切四边形边的关系。
求证：圆的外切四边形的两组对边的和相等．
已知：四边形ABCD是⊙O的外切四边形，切点分别是点P、L、M、N。
求证：AB+CD=AD+BC
证明：∵四边形ABCD是⊙O的外切四边形， 切点分别是点P、L、M、N。
∴AL=AP， BL=BM， CN=CM，DN=DP
∴AL+BL+CN+DN=AP+BM+CM+DP
即 AB+CD=AD+BC