初中数学第二章 直线与圆的位置关系2.3 三角形的内切圆说课课件ppt

这是一份初中数学第二章 直线与圆的位置关系2.3 三角形的内切圆说课课件ppt，共26页。PPT课件主要包含了⊙I就是所求的圆，读句画图，三边中垂线，三个角平分线，三角形内心的性质，一判断题，二填空，120°，在△OBC中，课堂小结等内容，欢迎下载使用。
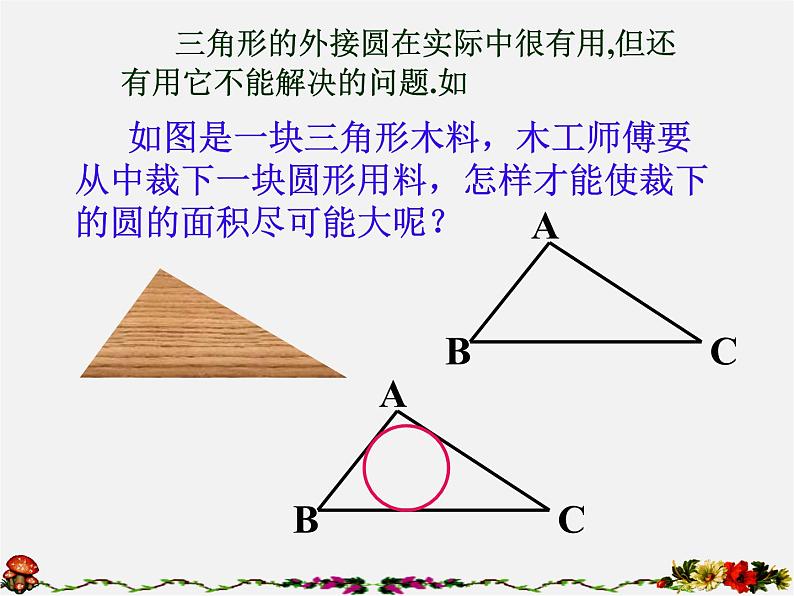
如图是一块三角形木料，木工师傅要从中裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？
三角形的外接圆在实际中很有用,但还有用它不能解决的问题.如
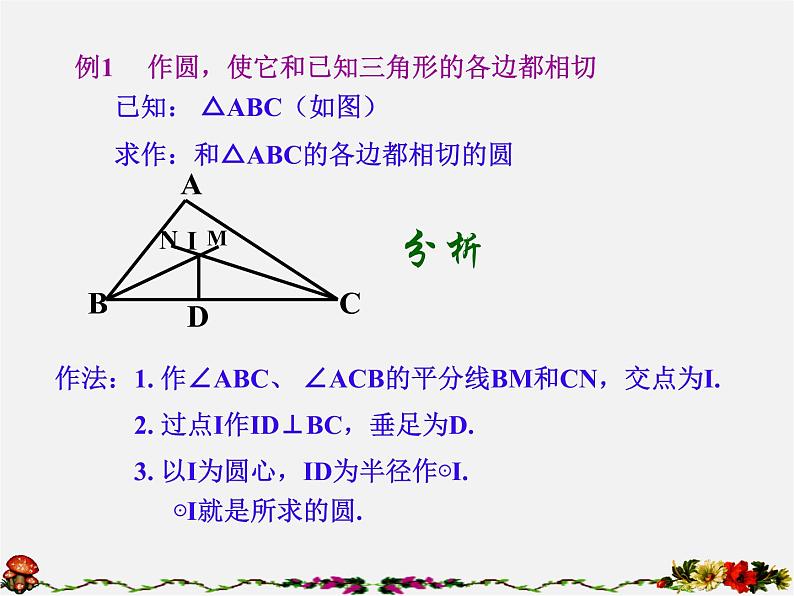
已知： △ABC（如图）求作：和△ABC的各边都相切的圆
作法：1. 作∠ABC、 ∠ACB的平分线BM和CN，交点为I.
例1 作圆，使它和已知三角形的各边都相切
2. 过点I作ID⊥BC，垂足为D.
3. 以I为圆心，ID为半径作⊙I.
1. 和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形.
2. 和多边形各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形.
②作直线m与⊙O相切于点D，作直线n与⊙O相切于点E，直线m和直线n相交于点A;
①以点O为圆心，1cm为半径画⊙O;
③作直线l与圆O相切于点F，直线l分别与直线m、直线n相交于点B、C.
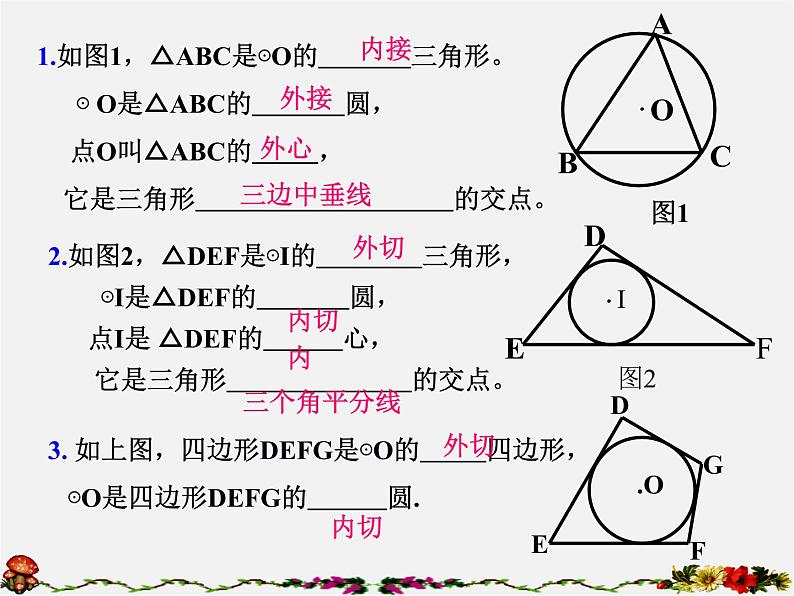
1.如图1，△ABC是⊙O的 三角形。 ⊙ O是△ABC的 圆， 点O叫△ABC的 ， 它是三角形 的交点。
2.如图2，△DEF是⊙I的 三角形， ⊙I是△DEF的 圆， 点I是 △DEF的 心， 它是三角形 的交点。
3. 如上图，四边形DEFG是⊙O的 四边形， ⊙O是四边形DEFG的 圆.
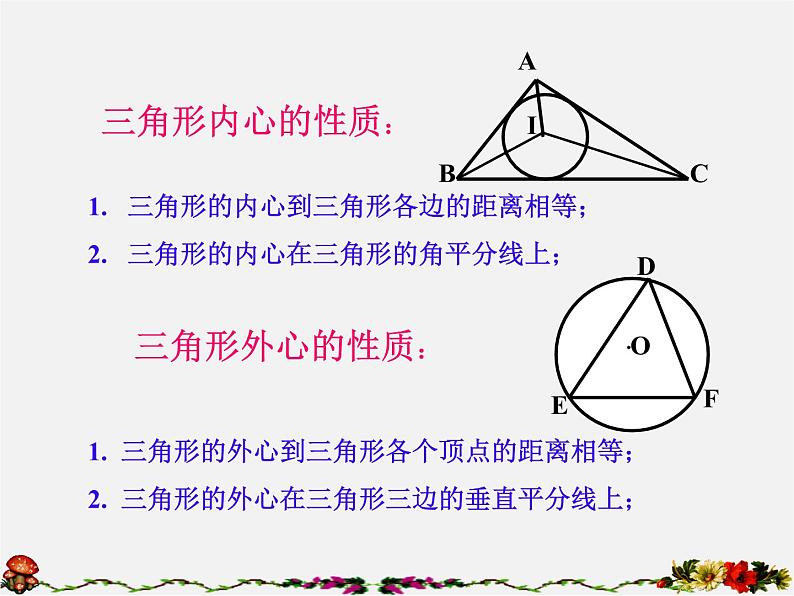
1. 三角形的内心到三角形各边的距离相等；2. 三角形的内心在三角形的角平分线上；
1. 三角形的外心到三角形各个顶点的距离相等； 2. 三角形的外心在三角形三边的垂直平分线上；
三角形外心的性质：
1. 三角形的内心到三角形各个顶点的距离相等（ ）2. 三角形的外心到三角形各边的距离相等 （ ）3. 等边三角形的内心和外心重合； （ ）4. 三角形的内心一定在三角形的内部（ ）5. 菱形一定有内切圆（ ）6. 矩形一定有内切圆（ ）
如图， △ABC的顶点在⊙O上， △ABC的各边与⊙I都相切，则△ABC是⊙I的 三角形；△ABC是⊙O的 三角形； ⊙I叫△ABC的 圆；⊙O叫△ABC的 圆，点I是△ABC的 心，点O是△ABC的 心
（2）若∠A=80 °，则∠BOC = 度。（3）若∠BOC=100 °，则∠A = 度。
（1）∵点O是△ABC的内心，
∴ ∠BOC=180 °－(∠1＋ ∠3)
= 180 °－(25°＋ 35 °)
理由： ∵点O是△ABC的内心，
（4）试探索： ∠A与∠BOC之间存在怎样的数量关系？请说明理由。
∠BOC =180 °－（ ∠1＋ ∠3 ）
1. 本节课从实际问题入手，探索得出三角形内切圆的作法 . 2. 通过类比三角形的外接圆与圆的内接三角形概念得出三角形的内切圆、圆的外切三角形概念，并介绍了多边形的内切圆、圆的外切多边形的概念。 3. 学习时要明确“接”和“切”的含义、弄清“内心”与“外心”的区别， 4. 利用三角形内心的性质解题时，要注意整体思想的运用，在解决实际问题时，要注意把实际问题转化为数学问题。
例2、如图，一个木摸的上部是圆柱，下部是底面为等边三角形的直棱柱．圆柱的下底面是圆是直三棱柱上底面等边三角形的内切圆．已知直三棱柱的底面等边三角形边长为３cm，求圆柱底面的半径。
例：直角三角形的两直角边分别是5cm，12cm .则其内切圆的半径为______。
已知：如图，在Rt△ABC中，∠C=90°，边BC、AC、AB的长分别为a、b、c，求求其内切圆O的半径长。
说出下列图形中圆与四边形的名称
四边形ABCD叫做⊙O的外切四边形
四边形ABCD叫做⊙O的内接四边形
探讨3： 设△ABC是直角三角形，∠C=90°，它 的内切圆的半径为r，△ABC 的各边长分别为a、b、c，试探讨r与a、b、c的关系.
已知：在△ABC中，BC=14，AC=9，AB=13，它的内切圆分别和BC、AC、AB切于点D、E、F，求AF、BD和CE的长。
∴(13-x)+(9-x)=14
略解：设AF＝x，则BF=13-x
由切线长定理知:AE=AF=x,BD=BF=13-x,DC=EC=9-x,又∵BD+CD=14
答：AF=4 BD=9 CE=5
∴AF=4，BD=9，CE=5
如图,O是△ABC的内心, ∠BAC与∠BOC有何数量关系? 试着作一推导.
1. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在圆的_______. 2.如图,O是△ABC的内心,则 OA平分∠______, OB平分∠______, OC平分∠______,.(2) 若∠BAC=100º,则∠BOC=______.
探讨2： 设△ABC 的内切圆的半径为r，△ABC 的各边长之和为L，△ABC 的面积S,我们会有什么结论?解:AD+AF+BD+BE+CE+CF=L 2AD+2BE+2CE=L 2AD=L－2（BE+CE） 　AD=ＡＥ＝？　　ＢＤ＝ＢＥ？　　ＣＥ＝ＣＦ＝？
三角形面积 （L为三角形周长，r为内切圆半径）
例3 如图，朱家镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑，以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等，AC⊥BC，BC=30米，AC=40米。请你帮助计算一下，镇标雕塑中心M离道路三边的距离有多远？
∵雕塑中心M到道路三边的距离相等∴点M是△ABC的内心，连结AM、BM、CM，设⊙M的半径为r米，⊙M分别切AC、BC、AB于点D、E、F，则MD⊥AC， ME ⊥BC， MF ⊥AB，则 MD= ME= MF=r，∵在Rt △ABC 中，AC=40，BC=30， ∴AB=50
思考 三条公路AB、AC、BC两两相交与A、B、C三点（如图所示）。已知AC⊥BC，BC=3千米，AC=4千米。现想在△ABC内建一加油站M，使它到三条公路的距离相等，请你帮助计算一下，加油站M应建在离公路多远的地方？
1.如图, ABC 的内心为I,外心为O.
(2)  BOC = 4BIC 360 °
2.如图,I是ABC的内心,连结AI并延长交BC边于点D,交ABC的外接圆于点E.
(1) EI = EB ;
(2)IE ² = AE · DE .