第八章 第五节 圆与圆的位置关系-备战2022年（新高考）数学一轮复习考点讲解+习题练习学案

第五节 圆与圆的位置关系及圆的应用

知识回顾  

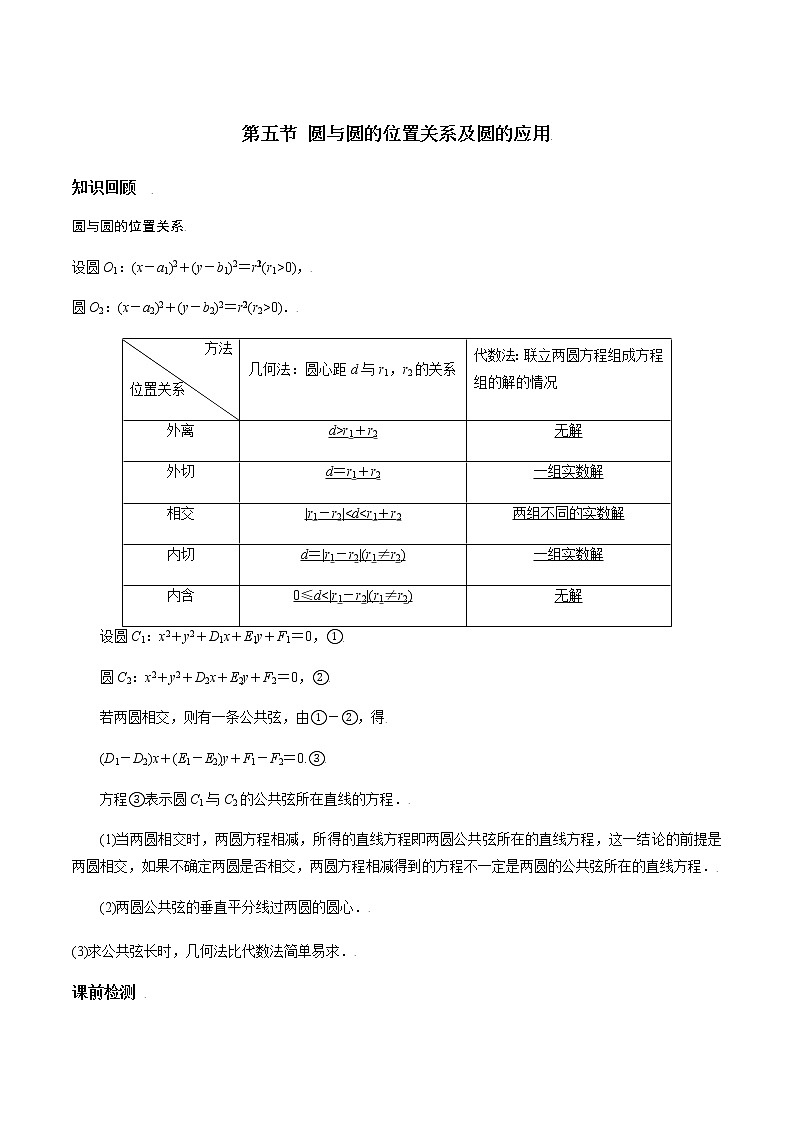
圆与圆的位置关系

设圆O1：(x－a1)2＋(y－b1)2＝r(r1>0)，

圆O2：(x－a2)2＋(y－b2)2＝r(r2>0)．

设圆C1：x2＋y2＋D1x＋E1y＋F1＝0，①

圆C2：x2＋y2＋D2x＋E2y＋F2＝0，②

若两圆相交，则有一条公共弦，由①－②，得

(D1－D2)x＋(E1－E2)y＋F1－F2＝0.③

方程③表示圆C1与C2的公共弦所在直线的方程．

(1)当两圆相交时，两圆方程相减，所得的直线方程即两圆公共弦所在的直线方程，这一结论的前提是两圆相交，如果不确定两圆是否相交，两圆方程相减得到的方程不一定是两圆的公共弦所在的直线方程．

(2)两圆公共弦的垂直平分线过两圆的圆心．

(3)求公共弦长时，几何法比代数法简单易求．

课前检测

1．圆C1：x2＋y2＋2x＝0，圆C2：x2＋y2＋4y＝0，则两圆的位置关系是________．

2．若圆C1：x2＋y2＝1与圆C2：x2＋y2＋6x－8y＋m＝0相切，则实数m的值为________．

3．（2020•山东新高考模拟卷）已知两定点，如果动点P满足，点Q是圆上的动点，则|PQ|的最大值为(    )

A． B． C． D．

4.圆心在直线x－y－4＝0上，且经过两圆x2＋y2＋6x－4＝0和x2＋y2＋6y－28＝0的交点的圆的方程为_________

5．两圆相交于两点A(1,3)和B(m，－1)，两圆圆心都在直线x－y＋c＝0上，则m＋c的值为________．

6．在平面直角坐标系xOy中，已知圆C1：(x－4)2＋(y－8)2＝1，圆C2：(x－6)2＋(y＋6)2＝9，若圆心在x轴上的圆C同时平分圆C1和圆C2的圆周，则圆C的方程是________．

课中讲解  

考点一.两圆位置关系的判定

例1.已知两圆x2＋y2－2x－6y－1＝0,x2＋y2－10x－12y＋m＝0.

(1)m取何值时两圆外切？

(2)m取何值时两圆内切？

(3)当m＝45时,求两圆的公共弦所在直线的方程和公共弦的长．

变式1 (2020·南京模拟)在平面直角坐标系xOy中，已知圆M：(x－a)2＋(y＋a－3)2＝1(a>0)，点N为圆M上任意一点．若以N为圆心、ON为半径的圆与圆M至多有一个公共点，则a的最小值为________．

例2.已知圆M：x2＋y2－2ay＝0(a＞0)截直线x＋y＝0所得线段的长度是2,则圆M与圆N：(x－1)2＋(y－1)2＝1的位置关系是(　　)

A．内切　　　　　　　B．相交

C．外切  D．相离

变式2.(1)圆C1：(x＋2)2＋(y－2)2＝4和圆C2：(x－2)2＋(y－5)2＝16的位置关系是(　　)

A．外离  B．相交  C．内切  D．外切

(2)圆x2＋y2＋4x－4y＋7＝0与圆x2＋y2－4x＋10y＋13＝0的公切线有________条．

例3.已知圆截直线所得线段的长度是，则圆与圆的位置关系是　　

A．内切 B．相交 C．外切 D．相离

考点二.两圆的公共弦问题

例1.若圆x2＋y2＝4与圆x2＋y2＋2ay－6＝0(a＞0)的公共弦长为2,则a＝________．

变式1.已知圆C：x2＋y2－10x－10y＝0与圆M：x2＋y2＋6x＋2y－40＝0相交于A，B两点．

(1)求圆C与圆M的公共弦所在直线的方程；

(2)求AB的长．

例2 (1)圆C1：x2＋y2－2x－8＝0与圆C2：x2＋y2＋2x－4y－4＝0的公共弦长为________．

(2)已知圆C1：x2＋y2－6x－6＝0，圆C2：x2＋y2－4y－6＝0，请判断两圆的位置关系，并说明两圆是否存在公共弦．若存在，求出公共弦所在直线的方程，若不存在，请说明理由．

变式2.（2020回民中学一模）已知圆与圆的公共弦所在的直线恒过定点，且点在直线上，则的取值范围是_____.

考点三.圆的应用

例1. 若动点P在直线上，动点Q在直线上，设线段PQ的中点为M，且≤8，则的取值范围是   ▲   .

变式1．如图，在平面直角坐标系xOy中，已知曲线C由圆弧C1和圆弧C2相接而成，两相接点M、N均在直线x＝5上，圆弧C1的圆心是坐标原点O，半径为13，圆弧C2过点A(29,0)．

(1)求圆弧C2的方程；

(2)曲线C上是否存在点P，满足PA＝PO？若存在，指出有几个这样的点；若不存在，请说明理由；

(3)已知直线l：x－my－14＝0与曲线C交于E、F两点，当EF＝33时，求坐标原点O到直线l的距离．

例2.如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．规划要求：新桥BC与河岸AB垂直，保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80 m．经测量，点A位于点O正北方向60 m处，点C位于点O正东方向170 m处(OC为河岸)，tan∠BCO＝.

(1)求新桥BC的长；

(2)当OM多长时，圆形保护区的面积最大？

课后习题

一．单选题

1．圆(x＋2)2＋y2＝4与圆(x－2)2＋(y－1)2＝9的位置关系为(　　)

A．内切   B．外切

C．相交   D．外离

2．圆C1：x2＋y2＝1与圆C2：x2＋(y－3)2＝1的内公切线有且仅有(　　)

A．1条  B．2条  C．3条  D．4条

3．两圆C1：x2＋y2＋2x－6y－26＝0，C2：x2＋y2－4x＋2y＋4＝0的位置关系是(　　)

A．内切   B．外切

C．相交   D．外离

4．(2020·盐城质检)若两圆x2＋y2＝m和x2＋y2＋6x－8y－11＝0有公共点，则实数m的取值范围是(　　)

A．(－∞，1)   B．(121，＋∞)

C．[1,121]   D．(1,121)

5．若点A(1,0)和点B(4,0)到直线l的距离依次为1和2，则这样的直线有(　　)

A．0条  B．1条  C．2条  D．3条

6．点P在圆C1：x2＋y2－8x－4y＋11＝0上，点Q在圆C2：x2＋y2＋4x＋2y＋1＝0上，则PQ的最小值是(　　)

A．3   B．3－5

C．3＋5   D．6

7.若圆C1：x2＋y2＝1与圆C2：x2＋y2－6x－8y＋m＝0外切,则m＝(　　)

A．21  B．19  C．9  D．－11

二．多选题

8．（2020•山东新高考模拟演练9）如图，，，，是以为直径的圆上一段圆弧，是以为直径的圆上一段圆弧，是以为直径的圆上一段圆弧，三段弧构成曲线W.则下述正确的是(    )

A．曲线W与x轴围成的面积等于；

B．曲线W上有5个整点(横纵坐标均为整数的点)；

C．所在圆的方程为：；

D．与的公切线方程为：.

三．填空题

9.设 x 、y均为正实数，且，以点为圆心,为半径的圆的面积最小时圆的标准方程为    ▲    

10.在平面直角坐标系中，已知点在曲线上，点在轴上的射影为.若点在直线的下方，当取得最小值时，点的坐标为           .

11．在平面直角坐标系xOy中，已知(x1－2)2＋y＝5，x2－2y2＋4＝0，则(x1－x2)2＋(y1－y2)2的最小值为________．

12．已知圆C1：(x－2)2＋(y－3)2＝1，圆C2：(x－3)2＋(y－4)2＝9，M，N分别是圆C1，C2上的动点，P为x轴上的动点，则PM＋PN的最小值为________．

13．已知圆O的半径为1，PA，PB为该圆的两条切线，A，B为两切点，那么·的最小值为________．

14．在平面直角坐标系xOy中，圆C：x2＋y2＝4分别交x轴正半轴及y轴负半轴于M，N两点，点P为圆C上任意一点，则·的最大值为____________．

15．(2020·南通模拟)在平面直角坐标系xOy中，圆C1：x2＋y2＝4，圆C2：x2＋y2＝16，点M(1,0)，动点P，Q分别在圆C1和圆C2上，满足MP⊥MQ，则线段PQ的取值范围是________．

16．在平面直角坐标系xOy中，点A(0,3)，若圆C：(x－a)2＋(y－a－2)2＝1上存在一点M满足MA＝2MO，则实数a的取值范围是________．

17．已知P点为圆O1与圆O2的公共点，圆O1：(x－a)2＋(y－b)2＝b2＋1与圆O2：(x－c)2＋(y－d)2＝d2＋1相交，若ac＝8，＝，则点P与直线l：3x－4y－25＝0上任意一点M之间的距离的最小值为________．

18.是圆外一动点，到圆上点的最短距离等于到直线的距离.

（1）求动点的轨迹的方程；

（2）点是直线上的动点，过点引曲线的两条切线，两条切线分别与轴交于两点，证明：以为直径的圆恒过定点.

19.如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2＋y2－12x－14y＋60＝0及其上一点A(2,4)．

(1)设圆N与x轴相切，与圆M外切，且圆心N在直线x＝6上，求圆N的标准方程；

(2)设平行于OA的直线l与圆M相交于B，C两点，且BC＝OA，求直线l的方程；

(3)设点T(t,0)满足：存在圆M上的两点P和Q，使得＋＝，求实数t的取值范围．

20．(2019·江苏五校联考)已知圆O1：x2＋y2－8x－8y＋48＝0，圆O2过点A(0，－4)．

(1)若圆O2与圆O1相切于点B(2，2)，求圆O2的方程；

(2)若圆O2过点C(4,0)，圆O1，O2相交于点M，N，且两圆在点M处的切线互相垂直，求直线MN的方程．