第七章 第二节 直线、平面的平行关系-备战2022年（新高考）数学一轮复习考点讲解+习题练习学案

这是一份第七章 第二节 直线、平面的平行关系-备战2022年（新高考）数学一轮复习考点讲解+习题练习学案，文件包含第七章第二节直线平面的平行关系原卷板docx、第七章第二节直线平面的平行关系解析版docx等2份学案配套教学资源，其中学案共42页， 欢迎下载使用。
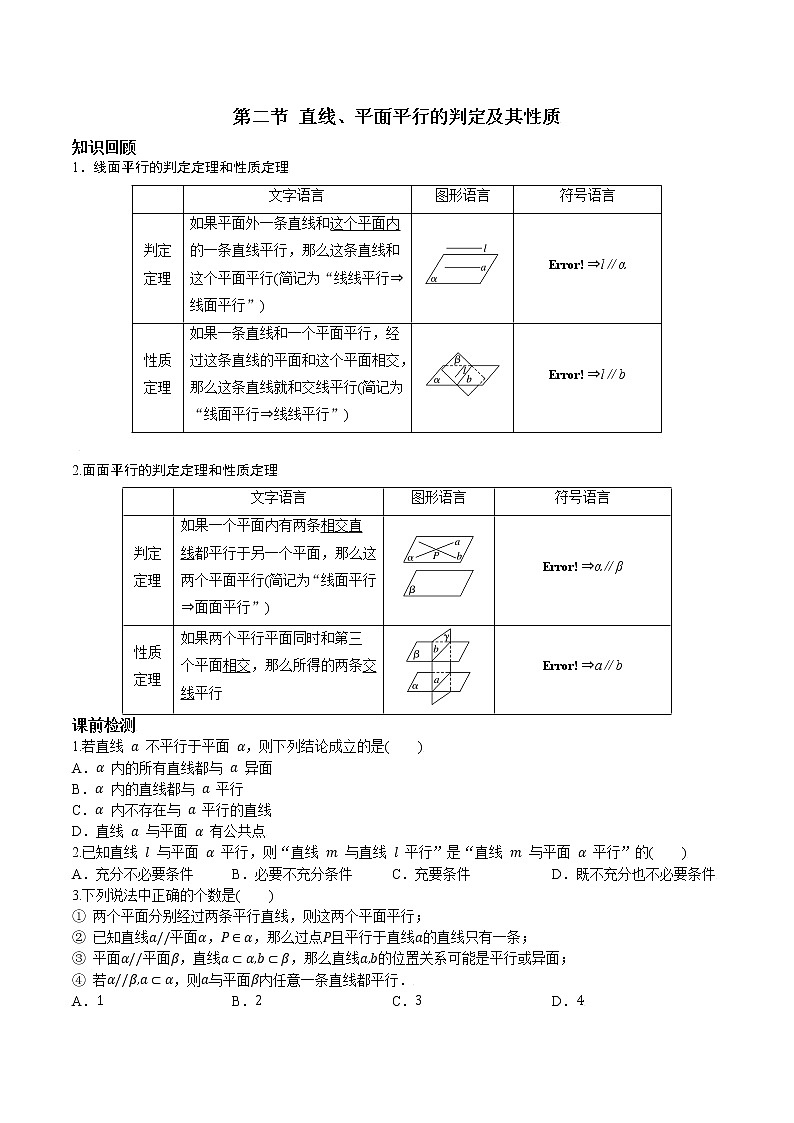
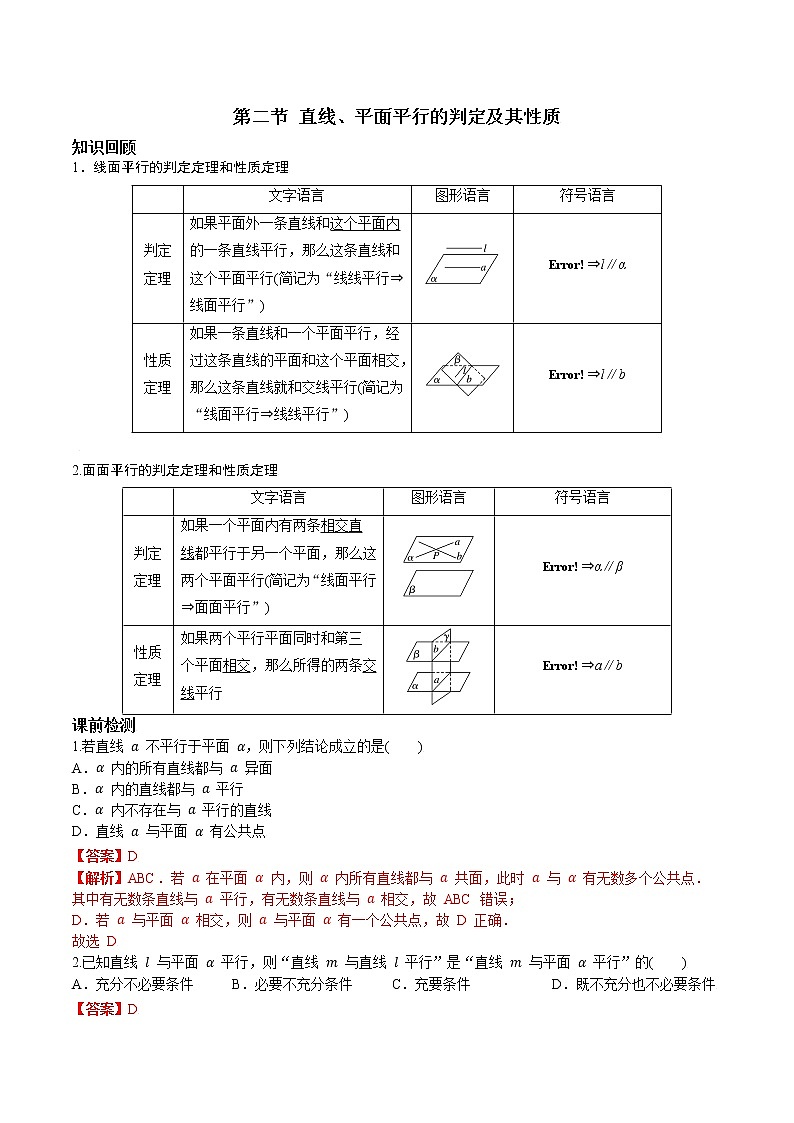
第二节 直线、平面平行的判定及其性质
知识回顾
1．线面平行的判定定理和性质定理

文字语言
图形语言
符号语言
判定定理
如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行(简记为“线线平行⇒线面平行”)

⇒l∥α
性质定理
如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行(简记为“线面平行⇒线线平行”)

⇒l∥b

2.面面平行的判定定理和性质定理

文字语言
图形语言
符号语言
判定定理
如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行(简记为“线面平行⇒面面平行”)

⇒α∥β
性质定理
如果两个平行平面同时和第三个平面相交，那么所得的两条交线平行

⇒a∥b
课前检测
1.若直线 a 不平行于平面 α，则下列结论成立的是(　　)
A．α 内的所有直线都与 a 异面
B．α 内的直线都与 a 平行
C．α 内不存在与 a 平行的直线
D．直线 a 与平面 α 有公共点
【答案】D
【解析】ABC．若 a 在平面 α 内，则 α 内所有直线都与 a 共面，此时 a 与 α 有无数多个公共点．
其中有无数条直线与 a 平行，有无数条直线与 a 相交，故 ABC 错误；
D．若 a 与平面 α 相交，则 a 与平面 α 有一个公共点，故 D 正确．
故选 D
2.已知直线 l 与平面 α 平行，则“直线 m 与直线 l 平行”是“直线 m 与平面 α 平行”的(　　)
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
【答案】D
【解析】由直线 l 与平面 α 平行，知：
“直线 m 与直线 l 平行”⇒“直线 m 与平面 α 平行或直线 m⊂ 平面 α”．
“直线 m 与平面 α 平行”⇒“直线 m 与直线 l 平行、相交或异面”．
∴“直线 m 与直线 l 平行”是“直线 m 与平面 α 平行”的既不充分也不必要条件．
故选 D
3.下列说法中正确的个数是(　　)
① 两个平面分别经过两条平行直线，则这两个平面平行；
② 已知直线a//平面α，P∈α，那么过点P且平行于直线a的直线只有一条；
③ 平面α//平面β，直线a⊂α,b⊂β，那么直线a,b的位置关系可能是平行或异面；
④ 若α//β,a⊂α，则a与平面β内任意一条直线都平行．
A．1 B．2 C．3 D．4
【答案】B
【解析】① 过两条平行直线的两个平面可能相交，故不正确；
② 由图可知：

正确
③ 两个平面平行，平面内的直线没有交点，根据空间图形两直线可能平行，可能异面，故正确；
④ 由图可知：

根据空间直线的位置关系，可知a与平面β内的直线可能异面．

4．设α，β是两个不同的平面，m，n是平面α内的两条不同直线，l1，l2是平面β内的两条相交直线，则α∥β的一个充分不必要条件是(　　)
A．m∥l1且n∥l2 B．m∥β且n∥l2
C．m∥β且n∥β D．m∥β且l1∥α
答案　A
解析　对于A，由m∥l1，m⊂α，l1⊄α，得l1∥α，同理l2∥α，又l1，l2相交，l1，l2⊂β，所以α∥β，反之不成立，所以m∥l1且n∥l2是α∥β的一个充分不必要条件．
5．若平面α∥平面β，直线a∥平面α，点B∈β，则在平面β内且过B点的所有直线中(　　)
A．不一定存在与a平行的直线
B．只有两条与a平行的直线
C．存在无数条与a平行的直线
D．存在唯一一条与a平行的直线
答案　A
解析　当直线a在平面β内且过B点时，不存在与a平行的直线，故选A.
6.(多选)下列命题正确的是(　　)
A．若直线与平面有两个公共点，则直线在平面内
B．如果两条异面直线中的一条与一个平面平行，则另一条直线一定与该平面相交
C．若直线l与平面α平行，则l与平面α内的直线平行或异面
D．若平面α∥平面β，直线a⊂α，直线b⊂β，则a∥b
【答案】AC　
【解析】 若直线与平面有两个公共点，由基本事实2可得直线在平面内，故A对；如果两条异面直线中的一条与一个平面平行，则另一条直线可能与该平面平行或相交或在平面内，故B错；若直线l与平面α平行，则l与平面α内的直线无公共点，即平行或异面，故C对；若平面α∥平面β，直线a⊂α，直线b⊂β，则a∥b或a，b异面，故D错．
7.(多选)如图，矩形ABCD中，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点，则在△ADE翻转过程中，下列命题正确的是(　　)
A．MB是定值
B．点M在圆上运动
C．一定存在某个位置，使DE⊥A1C
D．一定存在某个位置，使MB∥平面A1DE

【答案】ABD　
【解析】 取DC的中点N，连接MN，NB，则MN∥A1D，NB∥DE，∵MN∩NB＝N，A1D∩DE＝D，∴平面MNB∥平面A1DE，∵MB⊂平面MNB，∴MB∥平面A1DE，D正确；∠A1DE＝∠MNB，MN＝＝定值，NB＝DE＝定值，根据余弦定理得，MB2＝MN2＋NB2－2MN·NB·cos ∠MNB，∴MB是定值，A正确；∵B是定点，∴M在以B为圆心，MB为半径的圆上，B正确；当矩形ABCD满足AC⊥DE时存在，其他情况不存在，C不正确．∴A、B、D正确．

8.(一题两空)设α，β，γ是三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．
①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.
可以填入的条件有________(填序号)．
【答案】①或③
【解析】 由面面平行的性质定理可知，①正确；当m∥γ，n∥β时，n和m可能平行或异面，②错误；当n∥β，m⊂γ时，n和m在同一平面内，且没有公共点，所以m∥n，③正确．
课中讲解
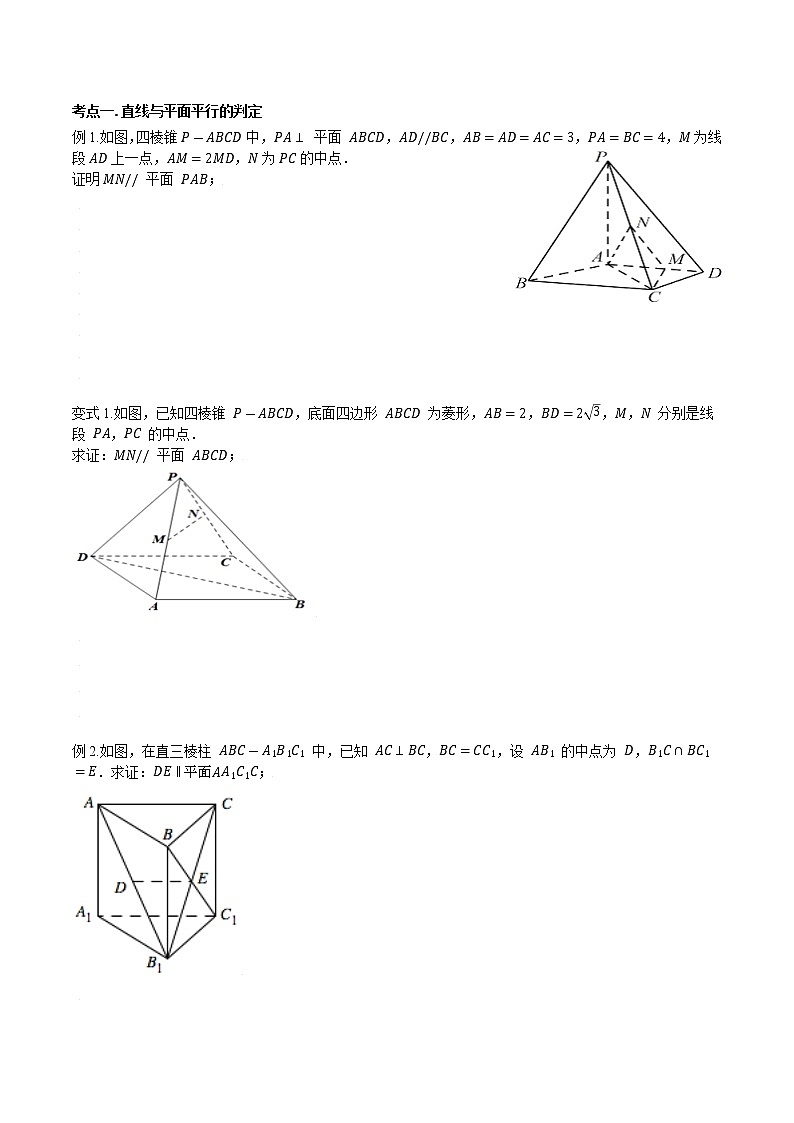
考点一.直线与平面平行的判定
例1.如图，四棱锥 P-ABCD 中，PA⊥ 平面 ABCD，AD//BC，AB=AD=AC=3，PA=BC=4，M 为线段 AD 上一点，AM=2MD，N 为 PC 的中点．
证明 MN// 平面 PAB；
【答案】见解析
【解析】取 BC 中点 E，连接 EN，EM；
因为 AD//BC，AB=3，BC=4，
所以 AM=BE，AMEB 为平行四边形，
所以 ME//AB，
又因为 NE 为三角形 PBC 中位线，
所以 NE//PB，
所以面 MNE// 面 PAB，
所以 MN// 平面 PAB．

变式1.如图，已知四棱锥 P-ABCD，底面四边形 ABCD 为菱形，AB=2，BD=23，M，N 分别是线段 PA，PC 的中点．
求证：MN// 平面 ABCD；
【答案】见解析
【解析】
连接 AC 交 BD 于点 O，
因为 M，N 分别是线段 PA，PC 的中点，
所以 MN//AC，
因为 MM⊂ 平面 ABCD，AC⊂ 平面 ABCD
所以 MN// 平面 ABCD．


例2.如图，在直三棱柱 ABC-A1B1C1 中，已知 AC⊥BC，BC=CC1，设 AB1 的中点为 D，B1C∩BC1=E．求证：DE∥平面AA1C1C；
【答案】略．
【解析】由题意知，E 为 B1C 的中点，
又 D 为 AB1 的中点，因此 DE∥AC．
又因为 DE⊄平面AA1C1C，AC⊂平面AA1C1C，
所以 DE∥平面AA1C1C 线面平行．
【备注】本题可通过证明 DE∥AC 来证明 DE∥面AA1C1C．

变式2.如图，在四棱锥P-ABCD中,∠ADC=∠PAB=90∘ ,BC=CD=12AD ,PA⊥CD,AD//BC,
试在棱PD上找一点E，使得直线CE//平面PAB，并说明理由；
【答案】E为PD中点
【解析】取PD中点E，中点F，连接EC,EF,FC，四边形ABEF为平行四边形∴CF//BA∴面CEF//面PAB∵CE⊂面CEF∴CE//面PAB；


例3.如图，在三棱锥 P-ABC 中，D，E，F 分别为棱 PC，AC，AB 的中点，已知 PA⊥AC，PA=6，BC=8，DF=5．
直线 PA// 平面 DEF；
【答案】见解析
【解析】因为 D，E 分别为棱 PC、AC 中点
所以 DE//PA．
又因为 PA⊄ 平面 DEF，DE⊆ 平面 DEF
所以直线 PA// 平面 DEF．


变式3.在直三棱柱ABC-A1B1C1中，∠BAC=90∘,AA1=AB=22AC=2，点P在线段BC上，且BP=12CP，点D是BB1的中点，且CD交于BC1点Q．证明：CC1//平面A1PQ；
【答案】见解析
【解析】∵ΔCC1Q∼ΔDBQ∴QDCQ=BDCC1=12∴QP//CC1∴CC1//平面A1PQ．


例4.如图，在三棱柱ABC-A1B1C1中，G为ABC的重心，BE=13BC1．求证：GE//平面ABB1A1；
【答案】见解析
【解析】证明：连结CG并延长交AB于O，过G作GD//AB，交BC于D，连接DE．如图所示．∵G为ABC的重心,∴BDBC=OGOC=13，又BEBC1=13，所以DE//CC1，又因为BB1//CC1，所以DE//BB1，∵DE⊄平面AA1B1B,BB1⊂ ⊂平面AA1B1B,∴DE//平面AA1B1B．∵GD⋂DE=D，且GD，DE⊂平面GDE，∴平面GDE//平面AA1B1B，又GE⊂平面GDE，所以GE//平面ABB1A1．

变式4.如图，四棱锥P­ABCD中，AD∥BC，AB＝BC＝AD，
E，F，H分别是线段AD，PC，CD的中点，AC与BE交于O点，G是线段OF上一点．求证：
(1)AP∥平面BEF；
(2)GH∥平面PAD.
证明：
(1)连接EC，
∵AD∥BC，BC＝AD，E是AD的中点，
∴BC綊AE，
∴四边形ABCE是平行四边形，
∴O为AC的中点．
又∵F是PC的中点，∴FO∥AP.
∵FO⊂平面BEF，AP⊄平面BEF，
∴AP∥平面BEF.
(2)连接FH，OH，
∵F，H分别是PC，CD的中点，
∴FH∥PD.
∵PD⊂平面PAD，FH⊄平面PAD，
∴FH∥平面PAD.
又∵O是AC的中点，H是CD的中点，∴OH∥AD.
又∵AD⊂平面PAD，OH⊄平面PAD，
∴OH∥平面PAD.
又∵FH∩OH＝H，∴平面OHF∥平面PAD.
又∵GH⊂平面OHF，∴GH∥平面PAD.
考点二.直线与平面平行的性质
例1.如图，平面五边形 ABCDE 中，AB//CE，且 AE=2，∠AEC=60∘，CD=ED=7，cos⁡∠EDC=57．将 △CDE 沿 CE 折起，使点 D 到 P 的位置，且 AP=3，得到四棱锥 P-ABCE，记平面 PAB 与平面 PCE 相交于直线 l，求证：AB//l．

【答案】见解析
【解析】∵AB//CE，且 CE⊂ 面 PCE．
∴AB// 面 PCE．
又 ∵ 面 PAB∩ 面 PCE=l．
∴AB//l．


变式1.如图，在底面是菱形的四棱锥 P-ABCD 中，PA⊥ 平面 ABCD，∠ABC=60∘，PA=AB=2，点 E、F 分别为 BC、PD 的中点，设直线 PC 与平面 AEF 交于点 Q．
已知平面 PAB∩ 平面 PCD=l，求证：AB//l；
【答案】见解析
【解析】∵AB//CD，AB⊄ 平面 PCD，CD⊂ 平面 PCD，
∴AB// 平面 PCD，∵AB⊂ 平面 PAB，平面 PAB∩ 平面 PCD=l，∴AB//l．

例2.如图：E、H分别是空间四边形ABCD的边AB、AD的中点，平面α过EH分别交BC、CD于F、G．
​​​
求证：EH//FG．
【答案】

略


【解析】证明：∵E、H分别是空间四边形ABCD的边AB、AD的中点；
∴EH//BD，
EH不在平面BCD内，BD在平面BCD内．
∴EH//平面BCD．
又平面α过EH分别交BC、CD于F、G；
∴EH//FG．
【备注】先根据条件得到EH//BD，进而得到EH//平面BCD，即可得到结论的证明．
本体主要考察直线与平面平行的性质.一般在证明线线平行时，常用方法为：证明线线平行或证明线面平行．
变式2.如图，ABEDFC 为多面体，平面 ABED 与平面 ACFD 垂直，点 O 在线段 AD 上，OA=1，OD=2，△OAB，△OAC，△ODE，△ODF 都是正三角形．
证明：直线 BC//EF；
【答案】见解析
【解析】
如图，设 G 是线段 DA 延长线 与线段 EB 延长线的交点．
由于 △OAB 与 △ODE 都是正三角形，
所以 OB//DE，OB=12DE，OG=OD=2，
同理，设 G' 是线段 DA 延长线与线段 FC 延长线的交点，有 OG'=OD=2，
又由于 G 和 G' 都在线段 DA 的延长线上，所以 G 与 G' 重合．
在 △GED 和 △GFD 中，
由 OB//DE，OB=12DE 和 OC//DF，OC=12DF，
可知 B，C 分别是 GE 和 GF 的中点，所以 BC 是 △GEF 的中位线，故 BC//EF．
考点三.面面平行的判定与性质
例1.如图，正方体 ABCD-A1B1C1D1 中，M，N，E，F 分别是 A1B1，A1D1，B1C1，C1D1 的中点．

(1) 求证：E，F，B，D 共面；
【答案】略
【解析】连接 B1D1，BD，EF．

∵EF∥B1D1，而 B1D1∥BD，
∴EF∥BD，
∴E，F，B，D 四点共面．

(2) 求证：平面 AMN∥平面EFDB．
【答案】略
【解析】连接 AM,AN,MN,DF,BE,FM，

∵FM=A1D1，FM∥A1D1，AD=A1D1，AD∥A1D1，
∴FM=AD，FM∥AD．
∴ 四边形 AMFD 为平行四边形，
∴AM∥DF，
又 ∵MN∥EF，且 AM∩MN=M，DF∩EF=F，
∴平面AMN∥平面EFDB．

变式1.如图，在平行六面体 ABCD-A1B1C1D1 中，E，F，G 分别是 A1D1，DD1，D1C1 的中点，证明：
​​​
(1) EG∥AC；
【答案】略
【解析】连接A1C1
∵E,G分别为A1D1,C1D1中点
∴EG∥A1C1∥AC

(2) 平面 EFG∥ 平面 AB1C．
【答案】见解析
【解析】由（1）EG∥AC，则 EG∥ 平面 AB1C
同理可得 EF∥B1C，则 EF∥ 平面 AB1C
又 EG∩EF=E，
所以平面 EFG∥ 平面 AB1C．
例2.如图，在矩形ABCD中，AB=3，BC=33，点E、H分别是所在边靠近B、D的三等分点，现沿着EH将矩形折成直二面角，分别连接AD、AC、CB，形成如图所示的多面体．
证明：平面BCE//平面ADH；
​​​
【答案】略
【解析】∵DH//CE，AH//BE，
DH∩AH=H，CE∩BE=E，
DH，AH⊂平面ADH，CE，BE⊂平面BCE，
∴平面BCE//平面ADH．
变式2.已知四棱锥 P-ABCD 中，底面 ABCD 是菱形，侧面 PAD⊥ 平面 ABCD，且 PA=3，AD=1，PD=2．若点 F 在线段 CD 上，且 DFFC=3，试问：在 PB 上是否存在一点 E，使 EF// 面 PAD？若存在，求出 PEEB 的值；若不存在，请说明理由．

【答案】存在，PEEB=3
【解析】存在 E，当 PEEB=3 时，使 EF// 面 PAD．
理由如下：
在 AB 上取一点 G，使 AGGB=3 时，则在 △PAB 中，PEEB=AGGB=3，
∴EG//AP，EG⊄ 平面 PAD，AP⊂ 平面 PAD，
∴EG// 平面 PAD，
∵ 在菱形 ABCD 中，AGGB=DFFC=3，
∴GF//AD，
同理，GF// 平面 PAD，
∵FG⊂ 平面 EFG，EG⊂ 平面 EFG，FG∩EG=G，
∴ 平面 EFG// 平面 PAD，
∴FG// 平面 PAD，
∵EF⊂ 平面 EFG，
∴EF// 平面 PAD．

例3.如图，在四棱柱 ABCD-A1B1C1D1 中，底面 ABCD 为等腰梯形，AB//CD，AB=4，BC=CD=2，AA1=2，E、E1 分别是棱 AD，AA1 的中点．设 F 是棱 AB 的中点，
证明：直线 EE1// 面 FCC1．

【答案】见解析
【解析】因为 F 为 AB 的中点，
CD=2，AB=4，AB//CD，
所以 CD//AF，
因此四边形 AFCD 为平行四边形，
所以 AD//FC．
又 CC1//DD1，FC∩CC1=C，
FC⊂ 平面 FCC1，CC1⊂ 平面 FCC1，
AD∩DD1=D，AD⊂ 平面 ADD1A1，
所以平面 ADD1A1// 平面 FCC1．
又 EE1⊂ 平面 ADD1A1，EE1⊄ 平面 FCC1，
所以 EE1// 平面 FCC1．
【备注】面面平行定义的应用，当不好做辅助线找线线平行，可先证明面面平行，再由定义应用得出线面平行．

变式3.如图所示，PA⊥ 平面 ABC，点 C 在以 AB 为直径的 ⊙O 上，∠CBA=30∘，PA=AB=2，点 E 为线段 PB 的中点，点 M 在 AB⏜ 上，且 OM//AC．求证：ME// 平面 PAC．

【答案】见解析
【解析】∵ 点 E 为线段 PB 的中点，点 O 为线段 AB 的中点
∴OE//PA．
∵PA⊂ 平面 PAC，OE⊄ 平面 PAC，
∴OE// 平面 PAC．
∵OM//AC，AC⊂ 平面 PAC，OM⊄ 平面 PAC，
∴OM// 平面 PAC．
∵OE⊂ 平面 MOE，OM⊂ 平面 MOE，OE∩OM=O，
∴ 平面 MOE// 平面 PAC．
∵ME⊂ 平面 MOE
∴ME// 平面 PAC．


考点四.平行关系的综合应用
例1.　如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．

(1)求证：AB∥平面EFGH，CD∥平面EFGH；
(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围．
(1)证明　∵四边形EFGH为平行四边形，
∴EF∥HG.
∵HG⊂平面ABD，EF⊄平面ABD，
∴EF∥平面ABD.
又∵EF⊂平面ABC，平面ABD∩平面ABC＝AB，
∴EF∥AB，又∵AB⊄平面EFGH，EF⊂平面EFGH，
∴AB∥平面EFGH.同理可证，CD∥平面EFGH.
(2)解　设EF＝x(0