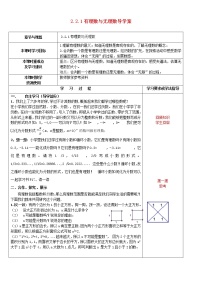
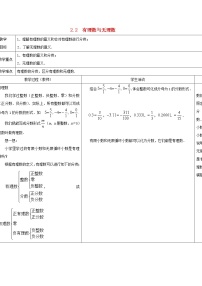
数学七年级上册2.2 有理数与无理数教学设计

这是一份数学七年级上册2.2 有理数与无理数教学设计，共2页。教案主要包含了生活情境创设，小组合作探究，数学知识建模，数学方法应用，课堂感悟等内容，欢迎下载使用。
2.2 有理数与无理数  教学目标1．理解有理数的意义和会对有理数进行分类；2．了解无理数的意义.教学重点1．有理数的意义和分类；2．无理数的意义．教学难点有理数的分类，区分有理数和无理数.一、生活情境创设我们学过整数（正整数、负整数、零）和分数（正分数、负分数）．实际上，所有整数都可以写成分母为1的分数的形式．如　我们把能写成分数形式（m、n是整数，n≠0）的数叫做有理数．想一想：小学里学过的有限小数和无限循环小数是有理数吗？，，，．有限小数和无限循环小数都可以化为分数，它们都是有理数．根据有理数的定义，有理数可以进行如下的分类：，或  二、小组合作探究1、议一议：是不是所有的数都是有理数呢？将两个边长为1的小正方形，沿图中红线剪开，重新拼成一个大正方形，它的面积为2．如果大正方形的边长为a，那么a2＝2．a是有理数吗？推导过程见书P15，（学生感受“无限夹逼法” ）2、事实上，a不能写成分数形式（m、n是整数，n≠0），a是无限不循环小数，它的值是1.414 213 562 373…．三、数学知识建模1、无限不循环小数叫做无理数．小学学过的圆周率π是无限不循环小数，它的值是3.141 592 653 589…，π是无理数．此外，像0.101 001 000 1…、－0.101 001 000 1…这样的无限不循环小数也是无理数．四、数学方法应用1、判断题. (1)无理数都是无限小数.             (2)无限小数都是无理数.(3)有理数与无理数的差都是有理数.  (4)两个无理数的和是无理数.2、将下列各数填入相应括号内：，，，，－2π，，．正数集合：{      　　     　　　　 …}；负数集合：{      　　     　　　　 …}；正有理数集合：{        　　　　　　 …}；负有理数集合：{      　   　　　　　 …}．3、以下各正方形的边长是无理数的是（      ）（A）面积为25的正方形；   (B)面积为16的正方形；(C)面积为3的正方形；      (D)面积为1.44的正方形.五、课堂感悟：                                                                     批注/记录