初中数学人教版八年级下册17.1 勾股定理优质课ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理优质课ppt课件，文件包含1711《勾股定理》课件25张pptx、1711《勾股定理》同步练习doc、1711《勾股定理》教学设计教案docx等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。

二次根式章末复习有理数
了解关于勾股定理的一些文化历史背景，会用面积法来证明勾股定理
会用勾股定理进行简单的计算
会用勾股定理进行简单的计算
关于直角三角形,你知道哪些方面的知识?
1.直角三角形叫Rt△2.两锐角互余∠A+∠B=90°3.三角形的面积s=1/2ab=1/2hc4. 30°所对的直角边等于斜边的一半5.证明两个直角三角形全等有“HL”
本节课我们再来探索直角三角形新的知识
请同学们欣赏下面海螺的图片：
在数学中也有这样一幅美丽的“海螺型”图案，如第七届国际数学教育大会的会徽。
这个图是怎样绘制出来的呢？
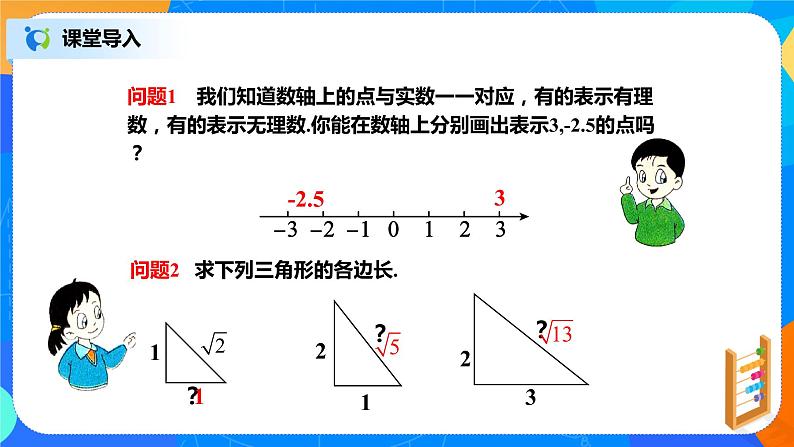
问题1 我们知道数轴上的点与实数一一对应，有的表示有理数，有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗？
问题2 求下列三角形的各边长.
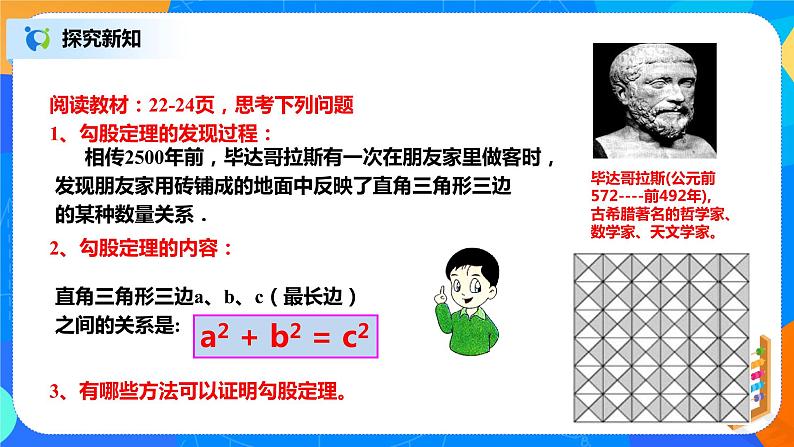
阅读教材：22-24页，思考下列问题1、勾股定理的发现过程：2、勾股定理的内容：3、有哪些方法可以证明勾股定理。
相传2500年前，毕达哥拉斯有一次在朋友家里做客时，发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系．
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。
直角三角形三边a、b、c（最长边）之间的关系是:
a2 + b2 = c2
设直角三角形的两条直角边长分别为a和b，斜边长为c.(1)已知a=6,c=10,求b；(2)已知a=5,b=12,求c;(3)已知c=25,b=15,求a.
　　由这三个正方形A，B，C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系？
　　探究一、三个正方形A，B，C 的面积有什么关系？　　
（图中每个小方格是1个单位面积）
1.A中含有____个小方格，即A的面积是 个单位面积．
B的面积是 个单位面积．
C的面积是 个单位面积．
结论：图1中三个正方形A，B，C的面积之间的数量关系是:
探究一、三个正方形A，B，C 的面积有什么关系？　　
探究二：SA+SB=SC在图2中还成立吗？
A的面积是 个单位面积．
B的面积是 个单位面积．
你是怎样得到正方形C的面积的？与同伴交流交流．
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?
至此，我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积，即SA+SB=SC
问题1:去掉网格结论会改变吗？
问题3:去掉正方形结论会改变吗？
　　想一想：在一般的直角三角形，以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系？
猜想：如果直角三角形两直角边长分别为a，b，斜边长为c，那么a2+b2=c2．
你有哪些方法可以证明？
如果直角三角形两直角边长分别为a，b，斜边长为c，那么a2+b2=c2．
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统”证法.
1.成立条件： 在直角三角形中；
3.作用：已知直角三角形任意两边长， 求第三边长.
（注意：哪条边是斜边）
全等三角形面积相等；底和高分别相等的一对三角形面积相等．
△ADB≌△ACG △BAG≌△BFC
当∠C=90°时，　 　　．
例：求出下列直角三角形中未知边的长度.
解：（1）在Rt△ABC中,由勾股定理得：AB2=AC2+BC2
（2）在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
1.求下列图中表示边的未知数x、y、z的值.
2.直角ABC的两直角边a=5,b=12,c=_____3.直角ABC的一条直角边a=10,斜边 c=26，则b= ______4.已知：∠C＝90°，a=6， a：b＝3：4，求b和c.
　1、本节课我们学到了什么？
　　通过本节课的学习我们不但知道了著名的勾股定理，还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想.
2、学了本节课后我们有什么感想？
　 很多的数学结论存在于平常的生活中，需要我们用数学的眼光去观察、思考、发现，这节课我们还受到了数学文化辉煌历史的教育.
教材24页练习1、2题