数学八年级下册18.1.1 平行四边形的性质优秀课件ppt

这是一份数学八年级下册18.1.1 平行四边形的性质优秀课件ppt，文件包含1812《平行四边形对角线的特点》课件44张pptx、1812《平行四边形对角线的特点》同步练习docx、1812《平行四边形对角线的特点》教学设计教案docx等3份课件配套教学资源，其中PPT共47页， 欢迎下载使用。

运用平行四边形的性质解决平面几何图形中求角的度数、证明线段相等、求点的坐标等问题
梳理知识，建立知识间的联系，形成知识结构，积累解决问题经验
发展推理论证能力、几何直观能力.
运用平行四边形的性质解决平面几何图形中的问题
运用平行四边形对角线性质求几何坐标
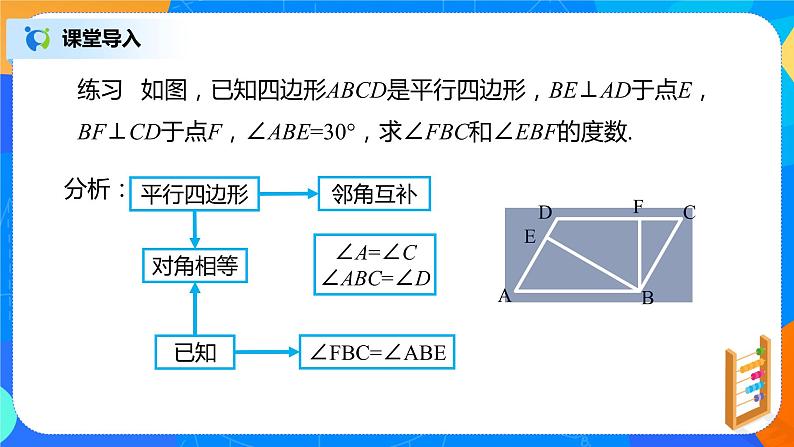
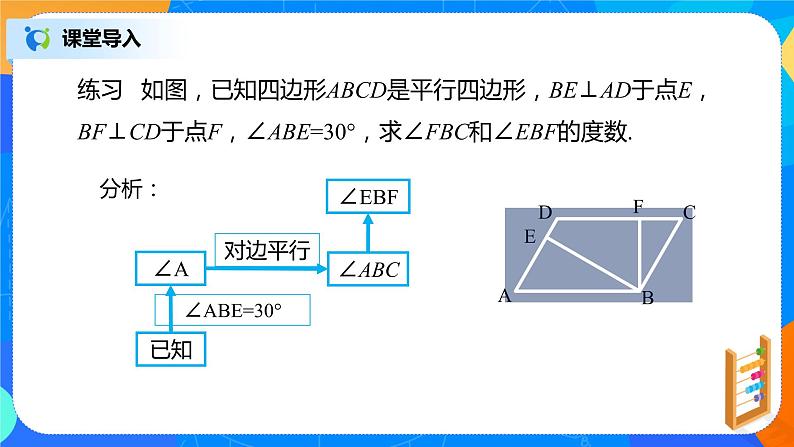
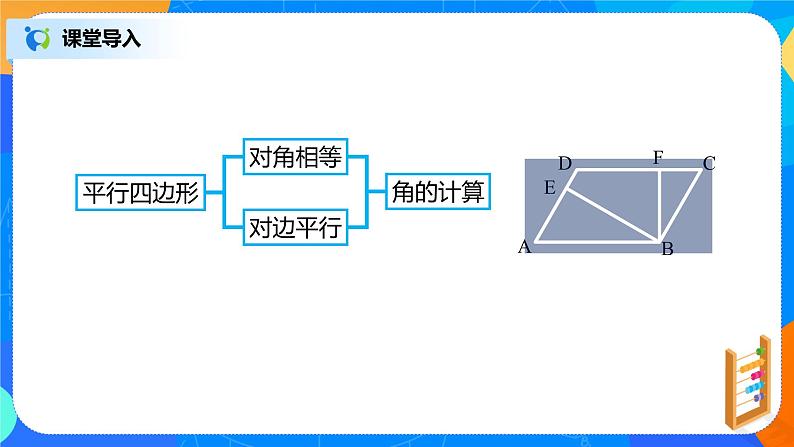
练习 如图，已知四边形ABCD是平行四边形，BE⊥AD于点E，BF⊥CD于点F，∠ABE=30°，求∠FBC和∠EBF的度数.
∠A=∠C∠ABC=∠D
解：∵四边形ABCD是平行四边形， ∴∠A=∠C，AD∥CB. ∵BE⊥AD，BF⊥CD，∴∠ABE=90°-∠A，FBC=90°-∠C.∴∠ABE=∠FBC.∵∠ABE=30°，∴∠FBC=30°.∵ BE⊥AD，∠ABE=30°，∴∠A=60°.又 ∠ABC=180°- ∠A，∴ ∠ABC=120°.∵ ∠EBF= ∠ABC- ∠ABE- ∠FBC， ∴ ∠EBF=60°.
例1 如图，四边形ABCD是平行四边形，O是对角线AC和BD的交点，过点O作直线EF分别交AB，CD于E，F两点.求证：OE=OF.
证明：∵ 四边形ABCD是平行四边形， ∴ AB∥CD，OB=OD.∴ ∠EBO=∠FDO， ∠BEO=∠DFO.∴ △BEO≌△DFO.∴ OE=OF.
对角线互相平分对边平行
思考：如果直线EF绕着点O转动，在转动的过程中， 是否始终有OE=OF？
证明：∵ 四边形ABCD是平行四边形， ∴ AB∥CD，OB=OD.∴ ∠EBO=∠FDO，∠BEO=∠DFO.∴ △BEO≌△DFO.∴ OE=OF.
变式 若直线EF与AD，CB的延长线分别交于点M，N ，线段DM和BN是否相等？
证明：∵ 四边形ABCD是平行四边形， ∴ AD∥CB，OD=OB.∴ ∠MDO=∠NBO，∠DMO=∠BNO.∴ △DMO≌△BNO.∴ DM=BN.
证明：∵ 四边形ABCD是平行四边形， ∴ AD∥CB，AD=CB，OA=OC.∴ ∠MAO=∠NCO， ∠AMO=∠CNO.∴ △AMO≌△CNO.∴ AM=CN.∵ DM=AM-AD，BN=CN-CB，∴ DM =BN.
证明：∵ 四边形ABCD是平行四边形， ∴ AB∥CD，AD∥CB，OB=OD，∠ADC=∠ABC.∴ ∠EBO=∠FDO，∠BEO=∠DFO.∴ △BEO≌△DFO.∴ BE=DF.又 ∠DMF=∠BNE，∠MDF=∠NBE.∴ △MDF≌△NBE.∴ DM=BN.
思考：如果直线EF绕着点O转动，在转动的过程中，直线EF始终与AD，CB的延长线相交，是否有DM = BN ？
AD∥CBAD=CBOA=OC
∠ADC=∠ABCAD∥CBOB=OD
例2 在平面直角坐标系xOy中，O是坐标原点，已知点A(2，0)，B(3，2) . 以O，A，B，C为顶点的平行四边形如图①， ②， ③所示，分别求出顶点C的坐标.
解：延长BC，交y轴于点D.∵ 四边形OABC是平行四边形， ∴ OA∥BC， OA=BC.∵ B(3，2)，∴ BD=3，点B到x轴的距离为2.又 点C在第一象限，∴ 点C的纵坐标为2.又 A(2，0)，∴ OA=2.∵ CD=BD-BC .∴ CD=1. ∴ 点C的横坐标为1.∴ 点C的坐标为(1，2).
解：分别过点B，C向x轴作垂线，垂足分别为M，N.∴∠AMB=∠ONC=90°.∵四边形OCAB是平行四边形， ∴AB∥OC， AB=OC.∴∠COA=∠BAO.∴∠CON=∠BAM.∴△CON≌△BAM.∴ON=AM，NC=MB.∵ B(3，2)，点C在第三象限，∴ 点C的纵坐标为-2.∵ A(2，0)，M(3，0)，∴ AM=1.∴ ON=1.∴ 点C的坐标为(-1，-2).
解：分别过点B，C向x轴作垂线，垂足分别为M，N.∵ 四边形OACB是平行四边形， ∴OA∥BC，OB∥AC， OB=AC.∴ BM=CN.又点B (3，2)，点C在第一象限， ∴点C的纵坐标为2.∵OB∥AC，∴∠BOM=∠CAN.又∠BMO=∠CNA=90°.∴△BOM≌△CAN. ∴OM=AN.∵M (3，0)，即OM=3，∴AN=3.又 A (2，0)，∴ON=OA+AN.即 ON=5.∴ N (5，0).∴ C (5，2).
在坐标系中研究几何图形
AE平分∠DABBF平分∠ABC
（1）证明： ∵ 四边形ABCD是平行四边形， ∴ AD∥BC. ∴ ∠DAB+∠ABC=180°. ∵ AE平分∠DAB，BF平分∠ABC， ∴ 2∠EAB+2∠FBA=180°. ∴ ∠EAB+∠FBA=90°. ∴ ∠AMB=90° . ∴ AE⊥BF.
（2）解： DF=CE，理由如下：∵四边形ABCD是平行四边形， ∴AB∥CD，AD=BC.∴∠DEA=∠EAB.又AE平分∠DAB， ∴∠DAE=∠EAB.∴∠DEA=∠DAE.∴DE=AD.同理 CF=BC.∴DE=CF.∵DF=DE-EF，CE=CF-EF，∴DF=CE.
1.如图，直线l1∥l2，△ABC与△DBC的面积相等吗？为什么？你还能画出一些与△ABC面积相等的三角形吗？
2.如图，平行四边形OABC的顶点O，A，C的坐标分别是(0，0)，(a，0)，(b，c).求顶点B的坐标.