人教版八年级下册18.1.1 平行四边形的性质获奖ppt课件

这是一份人教版八年级下册18.1.1 平行四边形的性质获奖ppt课件，文件包含1815《三角形的中位线定理》课件25页pptx、1815《三角形的中位线定理》同步练习doc、1815《三角形的中位线定理》教案教学设计docx等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。

平行四边形的判定（二）有理数
平行四边形的性质及判定定理的综合运用
理解三角形中位线的概念和定理的内容
进一步发展推理论证的能力
能利用三角形中位线定理解决有关证明和计算问题
理解三角形中位线的概念，掌握三角形的中位线定理
能利用三角形的中位线定理解决有关证明和计算问题
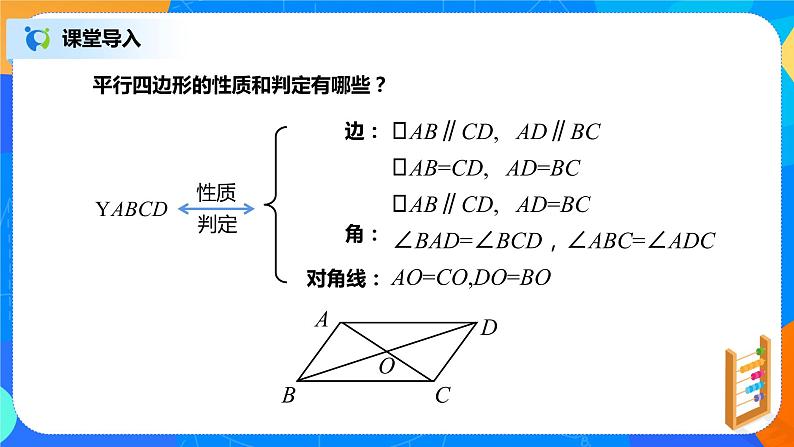
平行四边形的性质和判定有哪些？
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AD=BC
∠BAD=∠BCD，∠ABC=∠ADC
AO=CO,DO=BO
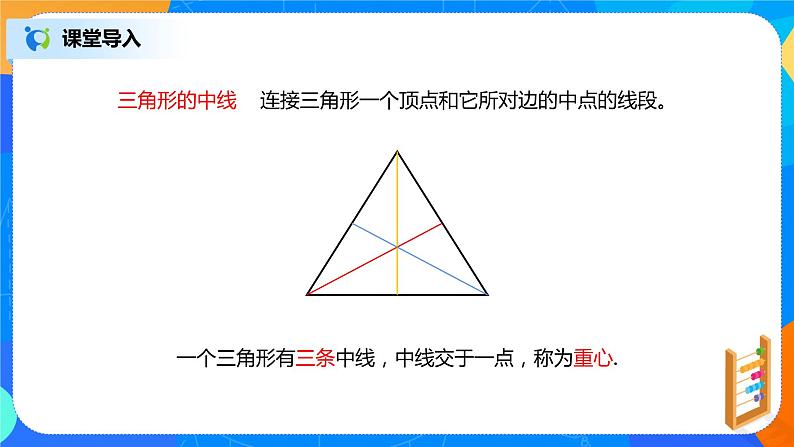
三角形的中线 连接三角形一个顶点和它所对边的中点的线段。
一个三角形有三条中线，中线交于一点，称为重心.
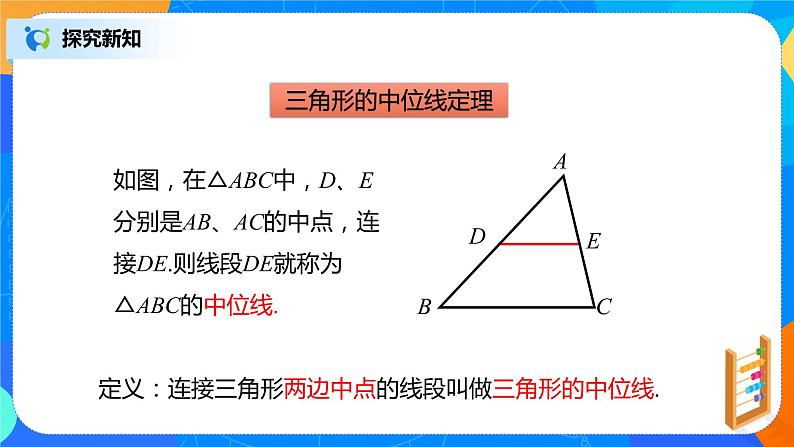
定义：连接三角形两边中点的线段叫做三角形的中位线.
如图，在△ABC中，D、E分别是AB、AC的中点，连接DE.则线段DE就称为△ABC的中位线.
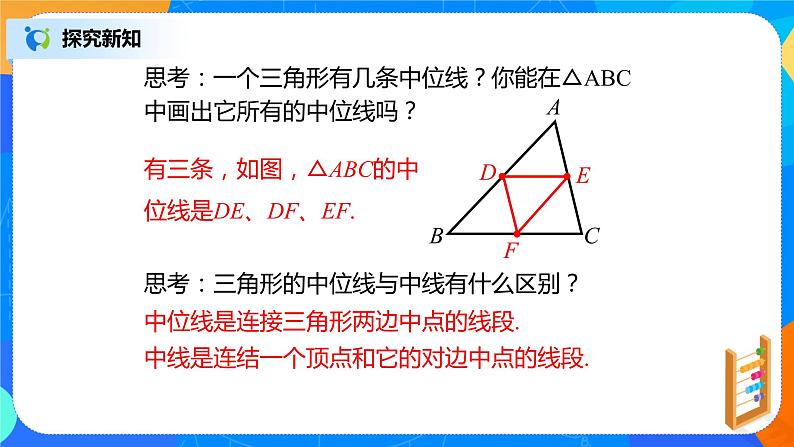
思考：一个三角形有几条中位线？你能在△ABC中画出它所有的中位线吗？
有三条，如图，△ABC的中位线是DE、DF、EF.
思考：三角形的中位线与中线有什么区别？
中位线是连接三角形两边中点的线段.
中线是连结一个顶点和它的对边中点的线段.
三角形中位线与三角形中线有什么区别？
（2）三角形的中位线与中线的区别主要是线段的端点不同．中位线是 点与 点的连线；中线是 点与对边 点的连线．
如图，DE是△ABC的中位线，DE与BC有怎样的关系？
一条线段是另一条线段的一半
证明：延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC，EF=DE
∴ CF∥DA，CF=DA
∴ CF∥BD，CF=BD
∴ DF∥BC，DF=BC
三角形的中位线平行于三角形的第三边，且等于第三边的一半。
∵DE是△ABC的中位线，
（ ∵AD=BD, AE=CE )
想一想：三角形的三条中位线围成的三角形的周长与原三角形的周长有什么关系？面积又有什么关系呢？
A、B两点被池塘阻隔，如何测两点距离？
在AB外选一点C，使C能直接到达A和B，连结AC和BC，并分别找出AC和BC的中点M、N。测出MN的长，就可知A、B两点的距离。
根据三角形的中位线定理，找到AB连线的中位线，如图MN所示。测出MN距离即可。
如果MN两点之间还有阻隔，你有什么解决办法？
1.如图，在△ABC中，D、E分别是AB，AC的中点，AC=12，F是DE上一点，连接AF，CF，若∠AFC=90°，EF=3DF，则BC的长为（　　）A．13B．14C．15D．16
分析：根据直角三角形的性质得到EF=6，根据EF=3DF，得到DF=2，求出DE，根据三角形中位线定理解答即可。
2.如图，点D、E、F分别为△ABC的三边的中点，若△DEF的周长是10，则△ABC的周长是（　　）A．5B．10C．15D．20
分析：根据三角形的中位线定理，△ABC的各边长等于△DEF的各边长的2倍，从而得出△ABC的周长。
3.如图，M、N分别是△ABC的边AC和AB的中点，D为BC上任意一点，连接AD，将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上，已知△AMN的面积为7，则图中阴影部分的面积为（　　）A．14 B．21C．28 D．7．
4.在△ABC中，AH⊥BC于H，D，E，F分别是BC，CA，AB的中点（如图所示）.求证：∠DEF=∠HFE．
分析：EF为中位线，所以EF∥BC，又因为∠HFE和∠FHB，∠DEF和∠CDE分别为一组平行线的对角，所以相等；转化成求证∠FHB=∠CDE．
解：∵E，F分别为AC，AB的中点，∴EF∥BC，根据平行线定理，∠HFE=∠FHB，∠DEF=∠CDE；同理可证∠CDE=∠B，∴∠DEF=∠B．又∵AH⊥BC，且F为AB的中点，∴HF=BF，∴∠B=∠BHF，∴∠HFE=∠B=∠DEF．即∠HFE=∠DEF。
1.在四边形ABCD中，ACBD相交于O点，AC=BD，E、F分别是AB，CD的中点，连接EF分别交AC、BD于M、N，判断三角形MON的形状，并说明理由．
分析：取BC边的中点G，连接EG，FG．根据三角形中位线定理得到GE=GF，根据平行线的性质和等量代换得到∠OMN=∠ONM，根据等腰三角形的判定定理证明结论．
2、三角形的中位线定理
三角形的中位线平行于三角形的第三边，且等于第三边的一半。