









- 18.2.2《矩形的判定》课件+教案+同步练习 课件 46 次下载
- 18.2.3《菱形的性质》课件+教案+同步练习 课件 48 次下载
- 18.2.5《正方形》课件+教案+同步练习 课件 48 次下载
- 18.2.6《正方形判定及应用》课件+教案+同步练习 课件 48 次下载
- 18.3.1《章末复习:专题讲解》课件+教案+同步练习 课件 51 次下载
初中数学人教版八年级下册18.2.2 菱形获奖ppt课件
展开掌握菱形判定方法;会用这些判定方法进行有关的论证和计算
根据菱形的判定定理进行简单的证明,培养学生的逻辑推理能力和演绎能力
在探究菱形判定方法的活动中获得成功的体验.通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心
根据菱形的判定定理进行简单的证明
会用这些判定方法进行有关的论证和计算
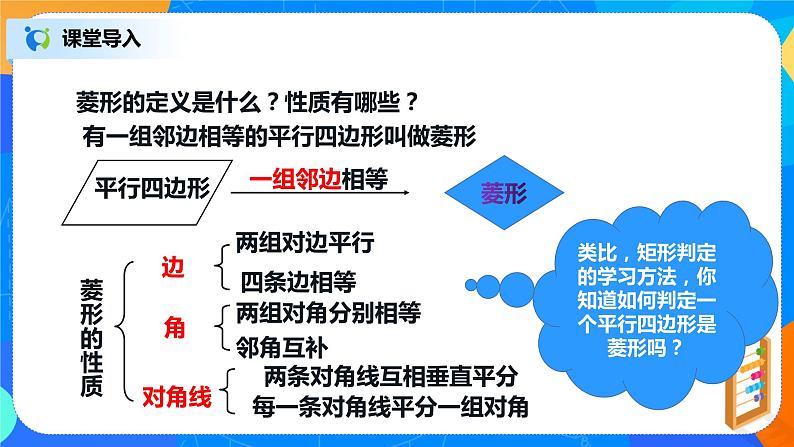
有一组邻边相等的平行四边形叫做菱形
两条对角线互相垂直平分每一条对角线平分一组对角
菱形的定义是什么?性质有哪些?
类比,矩形判定的学习方法,你知道如何判定一个平行四边形是菱形吗?
朋友的生日快到了,小丽想制作一个菱形的相框送给她,可是在制作完后遇到了困难,如何才能确定这个相框是不是菱形的呢?
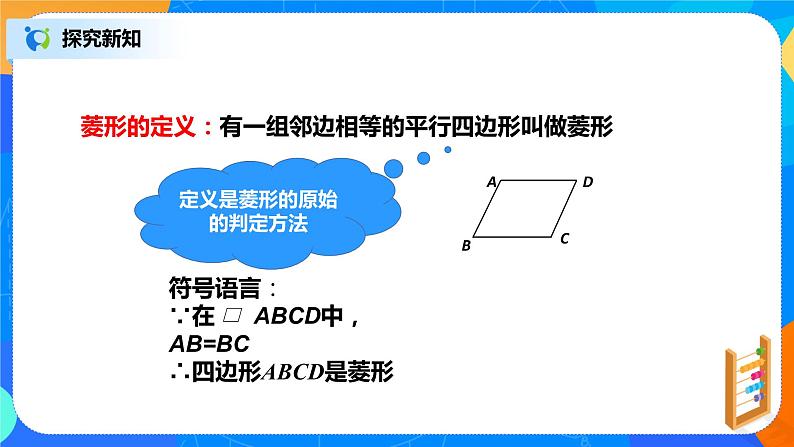
菱形的定义:有一组邻边相等的平行四边形叫做菱形
定义是菱形的原始的判定方法
符号语言:∵在 ABCD中,AB=BC∴四边形ABCD是菱形
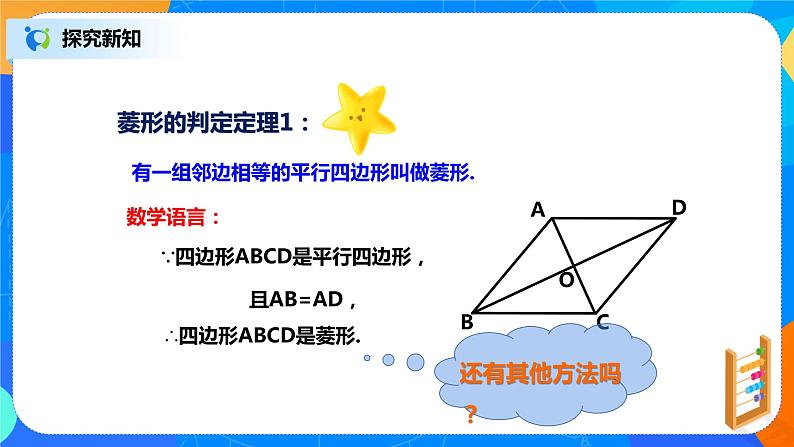
有一组邻边相等的平行四边形叫做菱形.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
对角线互相垂直的平行四边形是菱形。
菱形的对角线互相垂直。
命题:对角线互相垂直的平行四边形是菱形.
∵四边形ABCD是平行四边形
∴ 平行四边形ABCD是菱形
求证:平行四边形ABCD是菱形
已知:在平行四边形ABCD中,AC ⊥ BD
对角线互相垂直的平行四边形是菱形.
数学语言∵在□ABCD中,AC⊥BD
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.求证:四边形ABCD是菱形。
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
∴四边形ABCD是菱形
四条边都相等的四边形是菱形。
数学语言∵在四边形ABCD中AB=BC=CD=DA
例4: 如图,平行四边形ABCD的对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证: 平行四边形ABCD是菱形.
证明:∵AB=5,AO=4,BO=3,∴AB2=AO2+BO2∴△OAB是直角三角形, AC⊥ BD.∴ □ABCD是菱形.
1、判断题(1)对角线互相垂直的四边形是菱形( )(2)一条对角线垂直另一条对角线的四边形是菱形( )(3)对角线互相垂直且平分的四边形是菱形( )(4)对角线相等的四边形是菱形( )(5)对角线互相平分且邻边相等的四边形是菱形( )(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
2.四边形ABCD是矩形,MN垂直平分对角线BD于O,交AD于M,交BC于N,求证:四边形MBND是菱形。
分析:由矩形的性质得出∠MDO=∠NBO,由ASA证明△MOD≌△NOB,得出OM=ON,证出四边形MBND是平行四边形,再由MN⊥BD,即可得出结论
解析:∵四边形ABCD是矩形,∴AD∥BC,∴∠MDO=∠NBO,∵MN垂直平分对角线BD,∴OD=OB,MN⊥BD,在△MOD和△NOB中,∠MDO=∠NBO ;OD=OB ;∠MOD=∠NOB ,∴△MOD≌△NOB(ASA),∴OM=ON,∴四边形MBND是平行四边形,又∵MN⊥BD,∴四边形MBND是菱形.
3.已知,如图所示,在▱ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
分析:先证明四边形ABEF是平行四边形,再证明邻边相等即可得出结论
解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠AEB,∵∠BAD的平分线交BC于点E,∴∠DAE=∠BEA,∴∠BAE=∠BEA,∴AB=BE,同理:AB=AF,∴AF=BE,∵AF∥BE,∴四边形ABEF是平行四边形,∵AB=AF∴四边形ABEF是菱形。
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
1.数学课上,老师让同学们判断一个四边形是否为菱形,下面是某合作小组4位同学拟定的方案,其中正确的是( )A.测量对角线是否相等B.测量对角线是否垂直C.测量一组对角是否相等D.测量四边是否相等
2.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( )A.AB=BCB.∠ACB=60°C.∠B=60°D.AC=BC
3.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )A.若AC⊥BD,则平行四边形ABCD是菱形B.若BO=2AO,则平行四边形ABCD是菱形C.若AB=AD,则平行四边形ABCD是菱形D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
4.如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
解:∵四边形ABCD是平行四边形,∴AB=CD,∠A=∠C,∵DH=BG,∴AG=CH,在△AGE和△FHC中,AE=CF;∠A=∠C;AG=CH,∴△AGE≌△FHC(SAS),∴GE=FH,同理:GF=EH,∴四边形EGFH是平行四边形,又∵EF⊥GH,∴四边形EGFH是菱形.
5.如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.(1)求证:四边形EBFD是菱形;(2)已知AB=3,AD=9,求折痕EF的长
解析:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠BFE,由折叠的性质得:BE=DE,∠BEF=∠DEF,∴∠BEF=∠BFE,∴BE=BF,∴DE=BF,∵DE∥BF,∴四边形EBFD是平行四边形,又∵BE=DE,∴四边形EBFD是菱形;
人教版八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形优秀教学课件ppt: 这是一份人教版八年级下册<a href="/sx/tb_c88744_t3/?tag_id=26" target="_blank">第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形优秀教学课件ppt</a>,文件包含人教版数学八年级下册1824《菱形的判定》课件pptx、人教版数学八年级下册1824《菱形的判定》教学设计docx、人教版数学八年级下册1824《菱形的判定》导学案docx等3份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
初中数学湘教版八年级下册2.6.2菱形的判定优秀ppt课件: 这是一份初中数学湘教版八年级下册2.6.2菱形的判定优秀ppt课件,文件包含教学课件八下·湘教·26菱形第2课时菱形的判定pptx、262菱形的判定教案docx、262菱形的判定同步练习docx等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中华师大版2. 菱形的判定完美版课件ppt: 这是一份初中华师大版2. 菱形的判定完美版课件ppt,文件包含华东师大版中学数学八年级下192菱形第2课时菱形的判定教学课件pptx、第19章矩形菱形与正方形192菱形第2课时docx、1922菱形的判定同步练习docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。














