初中数学人教版八年级下册18.2.3 正方形优质ppt课件

这是一份初中数学人教版八年级下册18.2.3 正方形优质ppt课件，文件包含1826《正方形判定及应用》课件34页pptx、1826《正方形判定及应用》同步练习doc、1826《正方形判定及应用》教案教学设计docx等3份课件配套教学资源，其中PPT共37页， 欢迎下载使用。

探索并证明正方形的判定
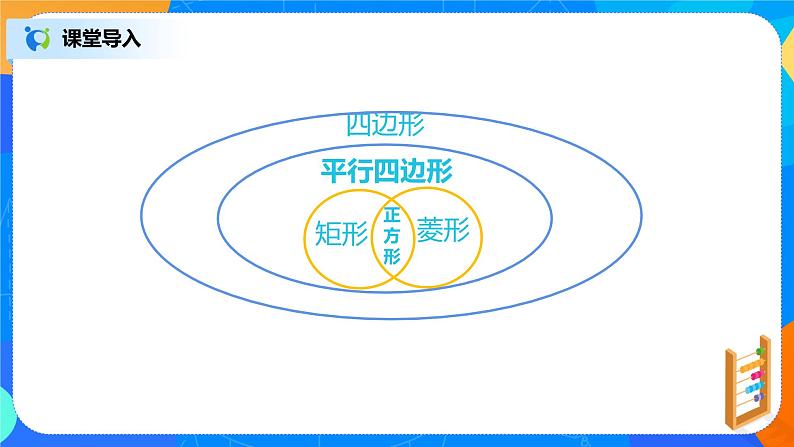
理解平行四边形、矩形、菱形之间的联系和区别
会运用正方形的判定条件进行有关的论证和计算
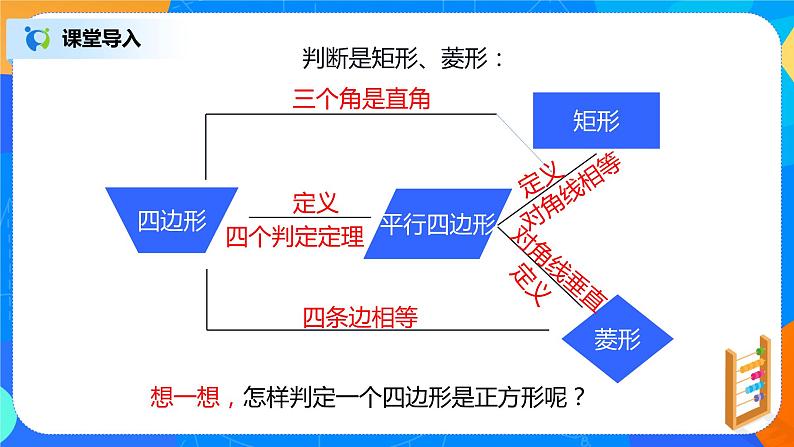
1.什么是正方形？2.正方形有哪些性质？3.我们是如何判断是矩形、菱形的？
想一想，怎样判定一个四边形是正方形呢？
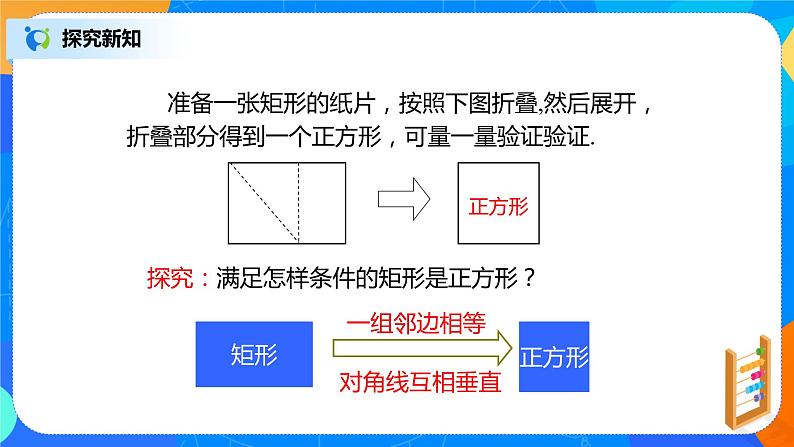
准备一张矩形的纸片，按照下图折叠,然后展开，折叠部分得到一个正方形，可量一量验证验证.
探究：满足怎样条件的矩形是正方形？
已知：如图,在矩形ABCD中,AC , DB是它的两条对角线, AC⊥DB.求证：四边形ABCD是正方形.证明：∵四边形ABCD是矩形, ∴ AO=CO=BO=DO ，∠ADC=90°. ∵AC⊥DB, ∴ AD=AB=BC=CD, ∴四边形ABCD是正方形.
对角线互相垂直的矩形是正方形.
把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状.量量看是不是正方形.
探究：满足怎样条件的菱形是正方形？
已知：如图,在菱形ABCD中,AC , DB是它的两条对角线, AC=DB.求证：四边形ABCD是正方形.证明：∵四边形ABCD是菱形,∴AB=BC=CD=AD,AC⊥DB.∵AC=DB,∴ AO=BO=CO=DO,∴△AOD,△AOB,△COD,△BOC是等腰直角三角形，∴∠DAB=∠ABC=∠BCD=∠ADC=90°, ∴四边形ABCD是正方形.
对角线相等的菱形是正方形.
类比 菱形的定义也是判定菱形的一种方法，那么正方形的定义也是判定正方形的一种方法.
平行四边形 + 一个角是直角一组邻边相等 = 正方形
矩形 + 一组邻边相等 = 正方形
菱形 + 一个角是直角 = 正方形
在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的是（ ）
A．AC=BD，AB∥CD，AB=CDB．AD∥BC，∠A=∠CC．AO=BO=CO=DO，AC⊥BDD．AO=CO，BO=DO，AB=BC
例1.已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
证明：∵ 四边形ABCD是正方形∴　 ∠A= ∠ B= ∠ C=∠D=90°，AB=AD=DC=BC（正方形的四条边都相等，四个角都是直角）．又∵ AE=BF=CG=DH∴AB-AE=AD-DH=DC-CG=BC-BF即BE=AH=DG=CF　∴ △AEH≌△BFE≌ △CGF ≌ △DHG．　 ∵ ∠1=∠3．又　 ∠3+∠2=90° ∠ ∠1+∠2=90°∴　 ∠EFH=90 °∴ 　 四边形EFGH是正方形（有一个角是直角的菱形是矩形）．
证明：∵ DE⊥AC，DF⊥AB ，∴∠DEC= ∠DFC=90°.又∵ ∠C=90 °，∴四边形ADFC是矩形.过点D作DG⊥AB，垂足为G.∵AD是∠CAB的平分线DE⊥AC，DG⊥AB，∴ DE=DG.同理得DG=DF，∴ED=DF，∴四边形ADFC是正方形.
例2 如图，在直角三角形中，∠C=90°，∠A、∠B的平分线交于点D.DE⊥AC，DF⊥AB.求证:四边形CEDF为正方形.
例3 如图，EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证：四边形EFGH是正方形.证明：∵四边形ABCD为正方形,∴OB=OC,∠ABO=∠BCO =45°,∠BOC=90°=∠COH+∠BOH.∵EG⊥FH,∴∠BOE+∠BOH=90°,∴∠COH=∠BOE,∴△CHO ≌△BEO,∴OE=OH.同理可证：OE=OF=OG,
∴OE=OF=OG=OH.又∵EG⊥FH,∴四边形EFGH为菱形.∵EO+GO=FO+HO ,即EG=HF,∴四边形EFGH为正方形.
例4.四边形ABCD是一块正方形场地，小华和小芳在AB边上取定了一点E，经测量EC=50m，EB=30m，这块场地的面积和对角线长分别是多少？
∵ 四边形ABCD是正方形
∴ ∠B=90°，AB=BC
∵ EC=50m，EB=30m
∴ S正方形ABCD=(40 )2=1600(m2)
前面学菱形时我们探究了顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形各边中点能得到菱形，那么顺次连接正方形各边中点能得到怎样的特殊平行四边形？
正方形的对角线的长度为8，求正方形的面积
解： 对角线×对角线×½ 所以 8×8×½=32
这公式又是从哪儿冒出来的呢？
解： 因为 ABCD是正方形 所以 OA=OB=OC=OD,AC⊥BD 又因为 AC=BD=8 所以OA=OB=OC=OD=4 在Rt△AOB中
矩形，菱形还有这种求面积公式么？
在一块正方形的花坛上，欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法？
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.下列正确的是（ ）Ａ. 四边相等的四边形是正方形Ｂ．四角相等的四边形是正方形Ｃ．对角线垂直的平行四边形是正方形Ｄ．对角线互相垂直平分且相等的四边形是正方形
2.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E，PF⊥BD于F,则PE+PF的长度为（ ）A.20 B.10 C.5 D.2
3.如图，已知E点在正方形ABCD的BC边的延长线上，且CE=AC，AE与CD相交于点F，则∠AFC的度数是（ ）A.92.5 ° B.102.5 ° C.112.5 ° D.122.5 °
4.以正方形ABCD的边DC向外作等边△DCE,则∠AEB的度数为（ ）A.15° B.30° C.45° D.60°
5.已知在平行四边形ABCD中，∠A=90°,如果添加一个条件，可使该四边形是正方形，那么这个条件可以是（ ）A．∠D=90° B.AD=BC C.BC=CD D. AB=CD
5.如图，△ABC中，D是BC上任意一点，DE∥AC，DF∥AB．（1）试说明四边形AEDF的形状，并说明理由．（2）连接AD，当AD满足什么条件时，四边形AEDF为菱形，为什么？
解：（1）∵DE∥AC，DF∥AB，∴四边形AEDF为平行四边形.（2）∵四边形AEDF为菱形，∴AD平分∠BAC，则AD平分∠BAC时，四边形AEDF为菱形.
（3）在（2）的条件下，当△ABC满足什么条件时，四边形AEDF为正方形，不说明理由．
解：由四边形AEDF为正方形∴∠BAC=90°，∴△ABC是以BC为斜边的直角三角形即可．
1.整理本节知识点 2.选做题： 同步检测题