初中数学人教版八年级下册19.1.2 函数的图象精品ppt课件

这是一份初中数学人教版八年级下册19.1.2 函数的图象精品ppt课件，文件包含1913《函数表示方法》课件25张pptx、1913《函数表示方法》同步练习doc、1913《函数表示方法》教案教学设计docx等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。

知道函数的三种表示法及其优缺点
能用适当的方式表示简单实际问题中的变量之间的函数关系
能对函数关系进行分析，对变量的变化情况进行初步讨论
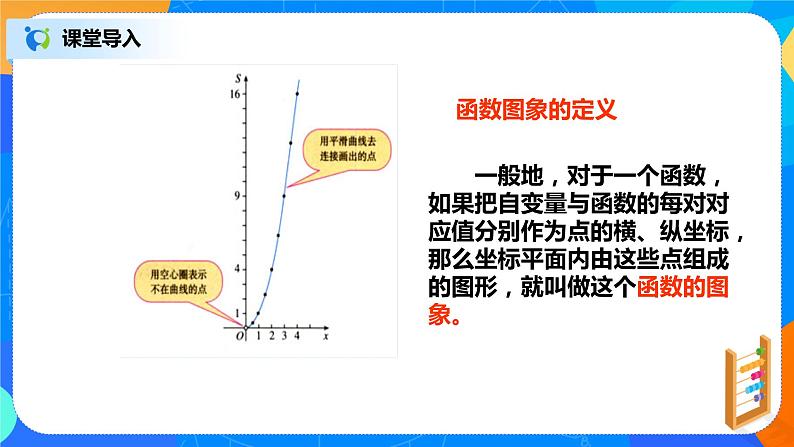
　　一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就叫做这个函数的图象。
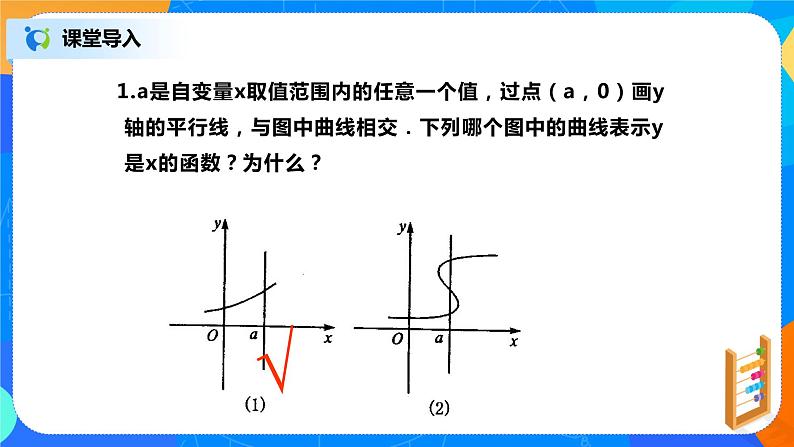
1.a是自变量x取值范围内的任意一个值，过点（a，0）画y轴的平行线，与图中曲线相交．下列哪个图中的曲线表示y是x的函数？为什么？
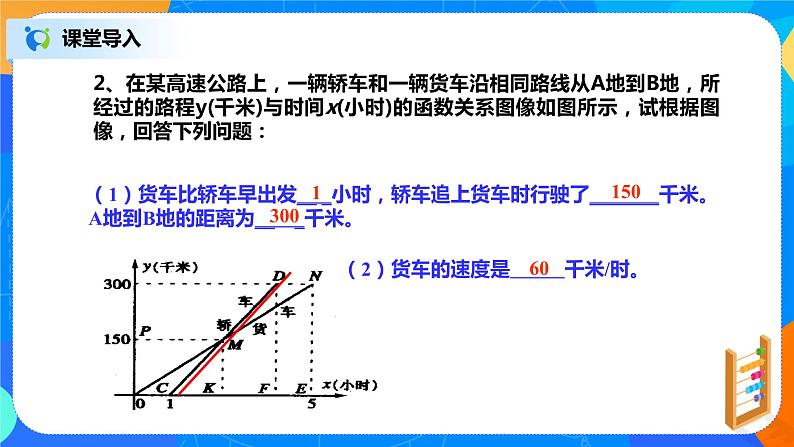
（1）货车比轿车早出发__ _小时，轿车追上货车时行驶了_______千米。A地到B地的距离为__ _千米。
2、在某高速公路上，一辆轿车和一辆货车沿相同路线从A地到B地，所经过的路程y(千米)与时间x(小时)的函数关系图像如图所示，试根据图像，回答下列问题：
（2）货车的速度是 千米/时。
探究1、下列式子中，对于 x 每一个确定的值，y 有唯一的对应值，即 y 是 x 的函数，请画出下列函数的图象．
画函数的图象三步曲：列表、描点、连线
描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点.
连线：把这些点用平滑的曲线连接起来.
从函数图像上可以看出，直线从左往右上升，即当x由小变大时，y=x+0.5随之增大
探究2、下列式子中，对于 x 每一个确定的值，y 有唯一的对应值，即 y 是 x 的函数，请画出下列函数的图象．
描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点。
连线： 把这些点用平滑的曲线连接起来。
从函数图象可以看出，曲线从左向右下降，即当x由小变大时， 随之减小。
描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点.
连线： 把这些点用平滑的曲线连接起来.
从函数图象可以看出，曲线从左向右下降，即当x由小变大时， 随之减小.
第一步：列表——表中给出一些自变量的值及其对应的函数值； 第二步：描点——在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点； 第三步：连线——按照横坐标由小到大的顺序，把所描出的各点用平滑曲线连接起来．
描点法画函数图象的一般步骤
想一想：通过这几节课的学习我们可以用什么方法表示函数呢？
你认为三种表示函数的方法各有什么优点呢？
例：一水库的水位在最近5 h 内持续上涨，下表记录了这5 h 内6 个时间点的水位高度，其中 t 表示时间，y表示水位高度．
（1）在平面直角坐标系中描出表中数据对应的点，这些点是否在一条直线上？由此你发现水位变化有什么规律？
可以看出，这6个点 ，且每小时水位上升0.3米.由此猜想，在这个时间段中水位可能是 以同一速度均匀上升的.
解：（1）如图，描出上表中数据对应的点．
由于水位在最近5小时内持续上涨，对于时间的每一个确定的值，水位高度都有 的值与其对应，所以，y t 的函数.函数解析式为：_______ 自变量的取值范围是： 它表示在这___小时内，水位匀速上升的速度为，这个函数可以近似地表示水位的变化规律.
（2）水位高度 y 是否为时间 t 的函数？如果是，试写出一个符合表中数据的函数解析式，并画出函数图象．这个函数能表示水位的变化规律吗？
（3）据估计这种上涨规律还会持续2 h，预测再过2 h水位高度将达到多少米．
由例题可以看出，函数的不同表示法之间可以转化.
如果水位的变化规律不变，按上述函数预测，再持续2小时，水位的高度： .此时函数图象（线段AB）向 延伸到对应的位置，这时水位高度约为 m.
1.如果A、B两人在一次百米赛跑中，路程（米）与赛跑的时间t（秒）的关系如图所示则下列说法正确的是（ ）
A. A比B先出发； B. A、B两人的速度相同； C. A先到达终点； D. B比A跑的路程多.
(2)点P(5，2)_____该函数的图象上(填“在”或“不在”).
3.已知火车站托运行李的费用C（元）和托运行李的重量P（千克）（P为整数）的对应关系如表：
（1）已知小周的所要托运的行李重12千克，请问小周托运行李的费用为多少元？（2）写出C与P之间的函数解析式.（3）小李托运行李花了15元钱，请问小李的行李重多少千克？
（1）小船与码头的距离是时间的函数吗？（2）如果是，写出函数的解析式，并画出函数图象.函数解析式为：
4.一条小船沿直线向码头匀速前进.在0min ，2min，4min，6min时，测得小船与码头的距离分别为200m，150m，100m，50m.
s = 200-25t
船速度（200-150÷2=25m/min
（3）如果船速不变，根据图像你能预测多长时间后小船到达码头？
解析：∵当s=0时， 200-25t=0， ∴25t=200， ∴t=8 故8分钟小船到达码头
（1）列表法：具体地反映了函数与自变量的数值对应关系。解析式法：准确地反映了函数与自变量之间的数量关系。图象法：直观地反映了函数随自变量的变化而变化的规律。（2）从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点．（3）函数的不同表示法之间可以 互换 。
教材81页练习1、2、3题