高中数学人教版新课标A必修22.1 空间点、直线、平面之间的位置关系教案配套ppt课件

这是一份高中数学人教版新课标A必修22.1 空间点、直线、平面之间的位置关系教案配套ppt课件，共14页。PPT课件主要包含了线线平行线面平行，求证MN∥面SAD，SMMC＝21，直线与平面平行的性质，线面平行的应用，线面平行线线平行，变式2，同理lb，高考题赏析等内容，欢迎下载使用。

例1:判断下列命题正确与否：(1)直线a与平面没有公共点，则直线a与平面平行.
(2)直线a与平面内的无数条直线不相交，直线a与平面平行.
(3)直线a与平面内的一条直线平行，则直线a与平面平行.
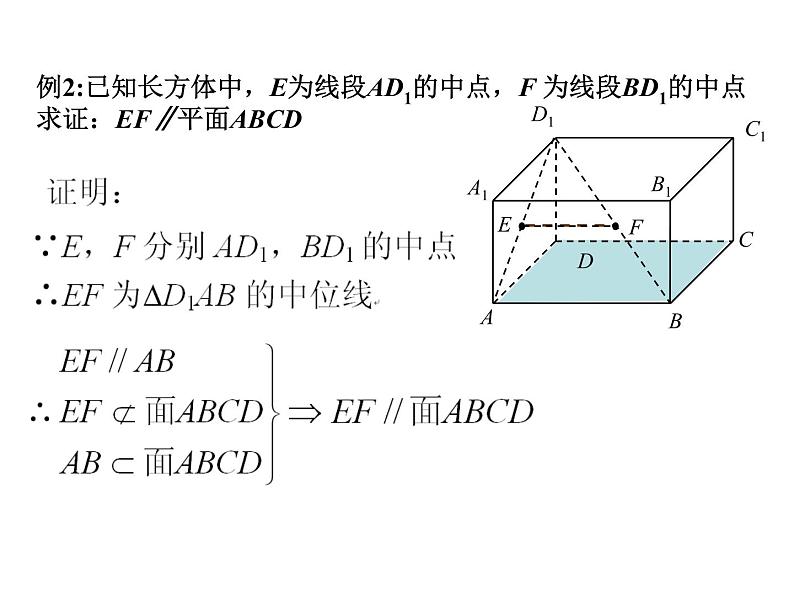
例2:已知长方体中，E为线段AD1的中点，F 为线段BD1的中点求证：EF∥平面ABCD
例3:如图所示，在正方体ABCD-A1B1C1D1中，M是BB1中点，证明：B1D//平面AMC
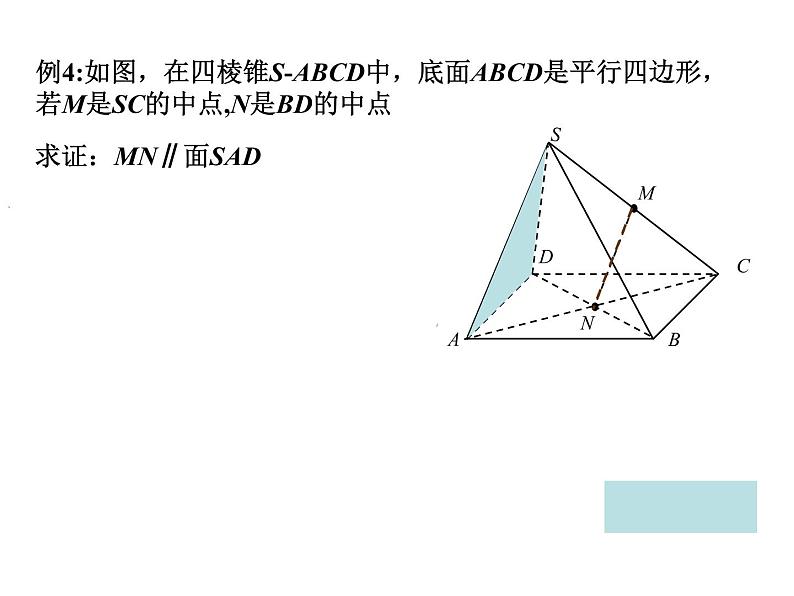
例4:如图，在四棱锥S-ABCD中，底面ABCD是平行四边形，若M是SC的中点,N是BD的中点
AB CD
变式1:如图，在四棱锥S-ABCD中，底面ABCD是平行四边形，M是SC上的中点，在AB上是否存在一点N, 使得MN∥面SAD？请证明你的结论
存在当N为AB中点时，MN//面SAD
作DS中点P，连结PM,PA
∵P,M分别为SD,SC的中点∴ PM//DC,且PM=0.5DC
∵ 四边形ABCD为平行四边形 ∴ AN//DC,且AN=0.5DC
∴四边形PMNA为平行四边形 ∴ MN//PA
推广:如图，在四棱锥S-ABCD中，底面ABCD是平行四边形，M是SC上的点，且SM：MC＝2：1，在AB上是否存在一点N,使得MN∥面SAD？请证明你的结论
若M是SC上任意一点？要如何考虑？
若a∥ , b  , 则a∥b或a、b异面
如图，在四棱锥S-ABCD中，底面ABCD是平行四边形，M是SC上的一个点，若SA∥面MBD,求证：M是SC的中点。
证明：连结AC交BD于点N，连结MN
变式3:在四棱锥S-ABCD木块中，底面ABCD是平行四边形，M是面SCB上的一个点，要经过M和棱AD将木块锯开，应该怎样划线？
设平面DMA∩平面SCB=PQ
如图所示，l∥ , l∥ , ∩=m , 求证：l∥m
如图，在直三棱柱ABC-A1B1C1中，E,F分别是AC1,BC1的中点，