初中数学2.2 圆的对称性教课课件ppt

这是一份初中数学2.2 圆的对称性教课课件ppt，共19页。PPT课件主要包含了想一想，做一做，③AM＝BM，AB是⊙O的一条弦，由①CD是直径，②CD⊥AB，垂径定理，如图小明的理由是，连接OAOB，则OA＝OB等内容，欢迎下载使用。
2.2 圆的对称性（2）
1．圆是什么对称图形？你是如何验证的？
　　（1）圆是中心对称图形，圆心是它的对称中心；　　（2）圆是轴对称图形，经过圆心的直线是它的对称轴．
　　2．圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少条对称轴？你是如何验证的？
1.圆既是中心对称图形，又是轴对称图形.
　　2.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
3.可利用折叠的方法即可解决上述问题.
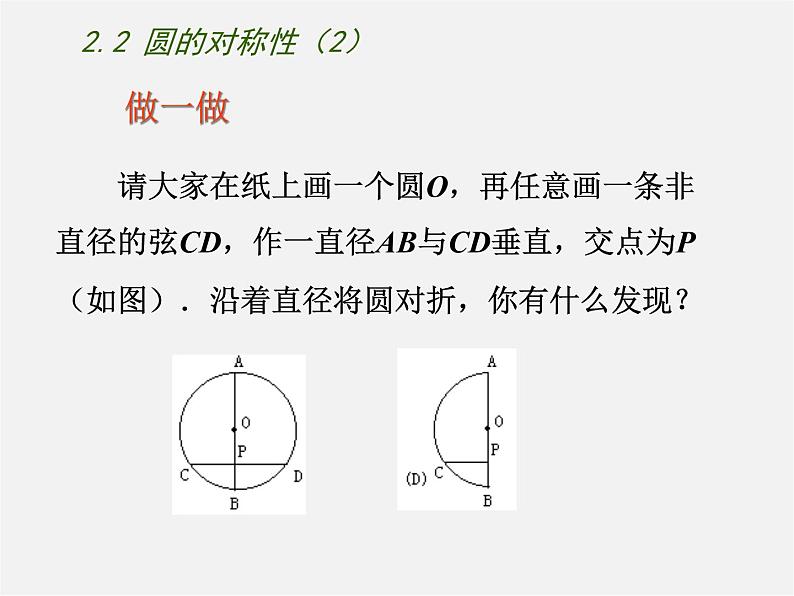
　　如何确定圆形纸片的圆心？动手试一试！
请大家在纸上画一个圆O，再任意画一条非直径的弦CD，作一直径AB与CD垂直，交点为P（如图）．沿着直径将圆对折，你有什么发现？
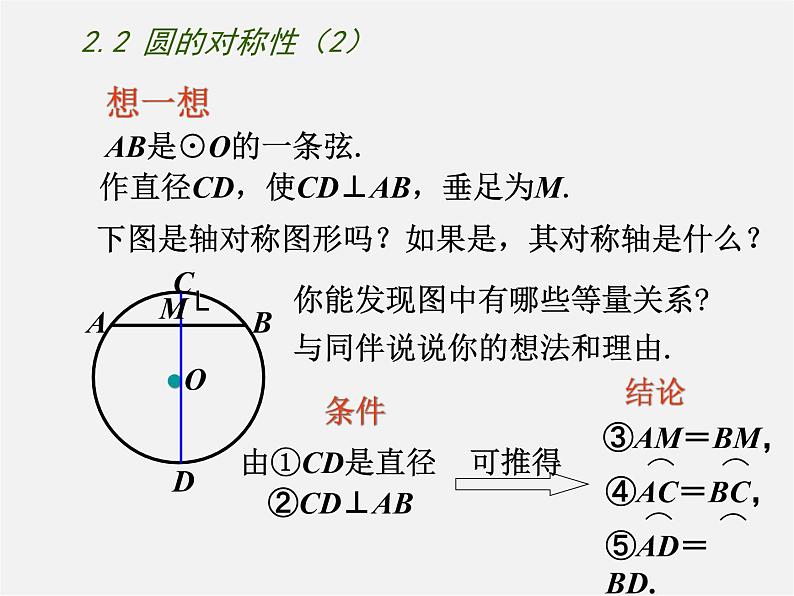
你能发现图中有哪些等量关系?与同伴说说你的想法和理由.
作直径CD，使CD⊥AB，垂足为M.
下图是轴对称图形吗？如果是，其对称轴是什么？
在Rt△OAM和Rt△OBM中,
∵OA＝OB，OM＝OM，
∴Rt△OAM≌Rt△OBM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时，点A与点B重合,
　　　定理：垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
老师提示：垂径定理是圆中一个重要的结论，三种语言要相互转化，形成整体，才能运用自如.
　　1．下列图形中，哪些能使用垂径定理，为什么？
　　2．如图，⊙O直径CD与弦AB（非直径）交于点M，添加一个条件：____________，就可得到点M是AB的中点．
　　例1　如图，已知在⊙O中，弦AB的长为8厘米，圆心O到AB的距离为3厘米，求⊙O的半径．
　　例2　如图，以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C、D．AC与BD相等吗？为什么？
　　1． “圆材埋壁”是我国古代著名数学家著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”此问题的实质是解决下面的问题：“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE＝1，AB＝10，求CD的长．”根据题意可得CD的长为________．
　　2． 已知⊙O的直径是50cm，弦AB∥CD，且AB＝40 cm，CD＝48 cm，求AB、CD之间的距离．
　　如图，AB、CD是⊙O的两条弦，AB∥CD，弧 AB与弧CD相等吗？为什么？
通过本节课的学习,你对圆的对称性有哪些认识？
课本P49第5、6、7、8.