九年级下册5.5 用二次函数解决问题教案配套课件ppt

这是一份九年级下册5.5 用二次函数解决问题教案配套课件ppt，共13页。PPT课件主要包含了复习旧知，拓展延伸，归纳小结，解这类题目的一般步骤，当堂反馈等内容，欢迎下载使用。

1、二次函数 的顶点坐标是 ，与x轴的交点坐标是 ，与y轴的交点坐标是 ；2、二次函数 的顶点坐标是 ，对称轴是 ，此函数有最 值为 。
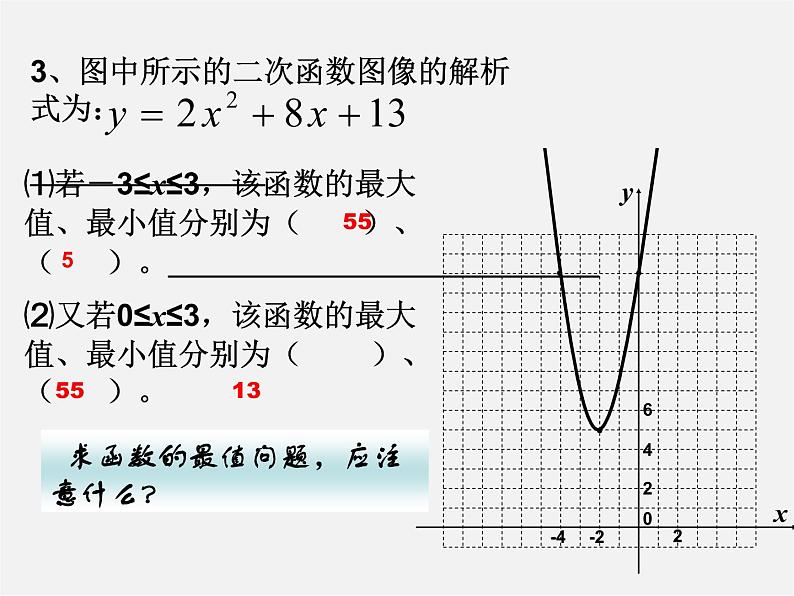
⑴若－3≤x≤3，该函数的最大值、最小值分别为（ ）、（ ）。
⑵又若0≤x≤3，该函数的最大值、最小值分别为（ ）、（ ）。
求函数的最值问题，应注意什么?
55
55 13
3、图中所示的二次函数图像的解析式为：
用一根36cm长的铁丝围成一个矩形（接头忽略不计），它的一边长为xcm.(1)写出这个矩形的面积S与边长x之间的函数关系式。(2)一边长x为何值时，矩形的面积S最大？最大值是多少？
某种粮大户去年种植水稻360亩，平均每亩收益440元，他计划今年多承租若干亩稻田。预计原360亩稻田平均每亩收益不变，新承租的稻田每增加1亩，其每亩平均收益比去年每亩平均收益少2元。该种粮大户今年应多承租多少亩稻田，才能使总收益最大？
分析：若设今年多承租X亩稻田，新承租的的稻田共收益 元；根据题意可得函数关系式： .
去年鱼塘里饲养鱼苗10千尾，平均每千尾的产量为1000千克，今年计划继续向鱼塘里投放鱼苗，预计每多投放1千尾，每千尾的产量将减少50千克，今年应投放鱼苗多少千尾，才能使总产量最大？最大总产量是多少？
室内通风和采光主要取决于门窗的个数和每个门窗的透光面积。如果计划用一段长12m的铝合金型材，制作一个上部是半圆、下部是矩形的窗框，那么当矩形的长、宽分别为多少时，才能使该窗户的透光面积最大（不计铝合金型材的宽度）？
如图，在ΔABC中，AB=8cm，BC=6cm，∠B＝90°，点P从点A开始沿AB边向点B以2厘米／秒的速度移动，点Q从点B开始沿BC边向点C以1厘米／秒的速度移动，如果P,Q分别从A,B同时出发，几秒后ΔPBQ的面积最大？最大面积是多少？
运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :
求出函数解析式和自变量的取值范围
配方变形，或利用公式求它的最大值或最小值。
检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
1、如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。(1)求S与x的函数关系式及自变量的取值范围；(2)当x取何值时所围成的花圃面积最大，最大值是多少？(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。
(1) ∵ AB为x米、篱笆长为24米 ∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
∴ S＝x（24－4x） ＝－4x2＋24 x （0∴ 0<24－4x ≤6 4≤x<6
∴当x＝4cm时，S最大值＝32 平方米
2、在矩形荒地ABCD中，AB=10，BC=6,今在四边上分别选取E、F、G、H四点，且AE=AH=CF=CG=x，建一个花园，如何设计，可使花园面积最大？
1.在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发，沿AB边向点B以1cm/秒的速度移动，同时，点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动，回答下列问题：（1）运动开始后第几秒时， △PBQ的面积等于8cm2（2）设运动开始后第t秒时， 五边形APQCD的面积为Scm2， 写出S与t的函数关系式， 并指出自变量t的取值范围；t为何值时S最小？求出S的最小值。