2021学年第4章 相交线与平行线4.4 平行线的判定图文课件ppt

这是一份2021学年第4章 相交线与平行线4.4 平行线的判定图文课件ppt，共33页。

1.掌握平行线的判定方法.(重点)2.灵活运用判定方法判定两直线平行,会正确书写简单的推理过程.(重点、难点)
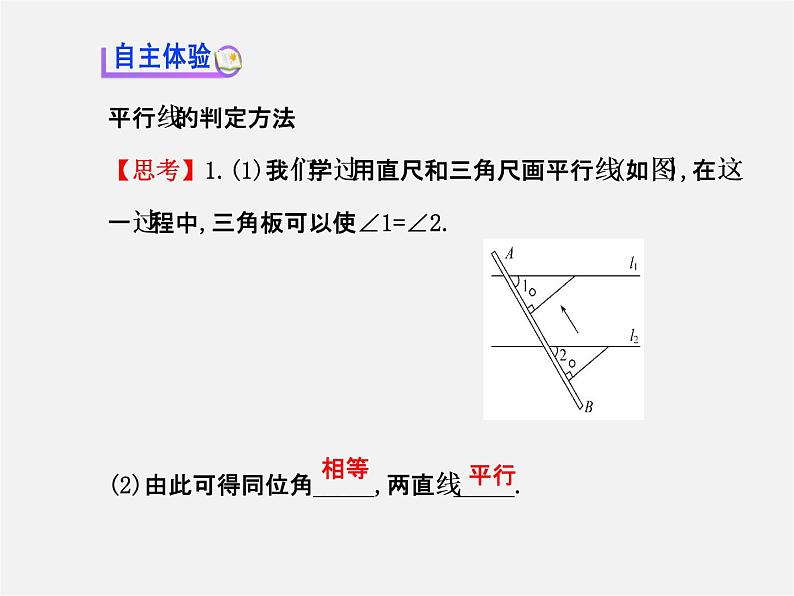
平行线的判定方法【思考】1.(1)我们学过用直尺和三角尺画平行线(如图),在这一过程中,三角板可以使∠1=∠2.(2)由此可得同位角_____,两直线_____.
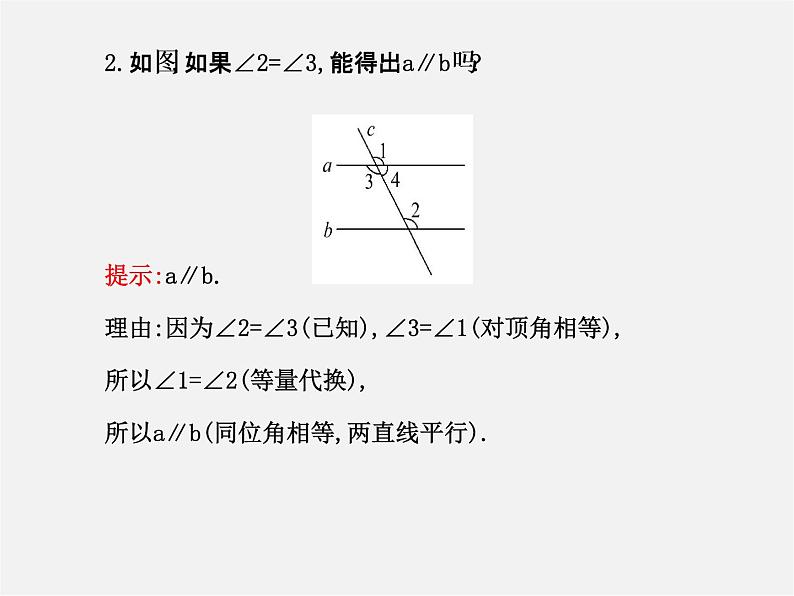
2.如图,如果∠2=∠3,能得出a∥b吗?提示:a∥b.理由:因为∠2=∠3(已知),∠3=∠1(对顶角相等),所以∠1=∠2(等量代换),所以a∥b(同位角相等,两直线平行).
3.问题2中,如果∠2+∠4=180°,能得出a∥b吗?提示:a∥b.理由:因为∠4+∠2=180°,∠4+∠1=180°(已知),所以∠2=∠1(同角的补角相等),所以a∥b(同位角相等,两直线平行).
【总结】平行线的判定方法:(1)同位角_____,两直线平行.(2)内错角_____,两直线平行.(3)同旁内角_____,两直线平行.
(打“√”或“×”)(1)内错角互补,两直线平行.( )(2)垂直于同一条直线的两条直线互相平行.( )(3)同旁内角相等,两直线平行.( )(4)利用直尺和三角板画已知直线的平行线的依据是“同位角相等,两直线平行”.( )
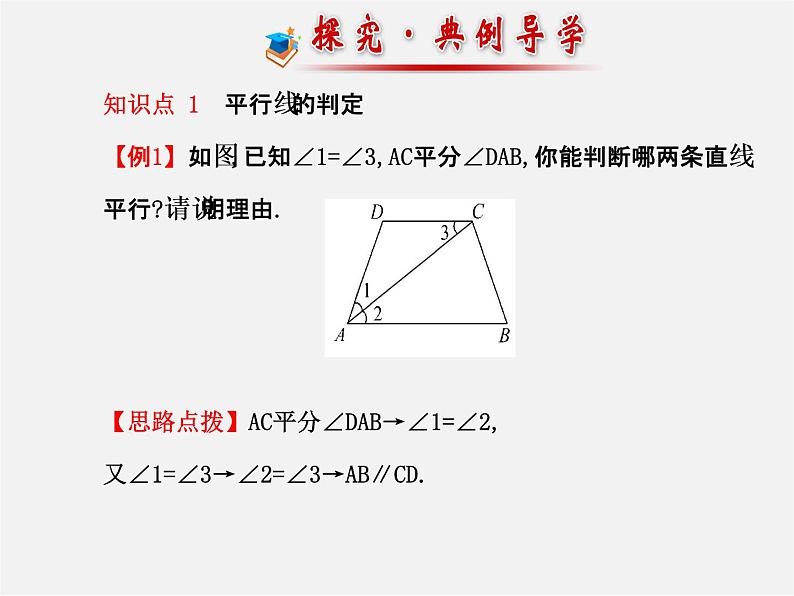
知识点 1 平行线的判定 【例1】如图,已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.【思路点拨】AC平分∠DAB→∠1=∠2,又∠1=∠3→∠2=∠3→AB∥CD.
【自主解答】AB∥CD.理由:因为AC平分∠DAB(已知),所以∠1=∠2(角平分线定义),又因为∠1=∠3(已知),所以∠2=∠3(等量代换),所以AB∥CD(内错角相等,两直线平行).
【总结提升】平行线判定的六种方法①同一平面内,不相交也不重合的两条直线互相平行;②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;③同一平面内,垂直于同一条直线的两条直线互相平行;④同位角相等,两直线平行;⑤内错角相等,两直线平行;⑥同旁内角互补,两直线平行.
知识点 2 平行线的性质与判定的综合应用 【例2】(2013·广安中考)如图,若∠1=40°,∠2=40°,∠3=116°30',则∠4=　　　　.【思路点拨】先根据∠1=∠2可以判定a∥b,再根据平行线的性质可得∠3与∠4上方的邻补角相等,再根据邻补角互补可得答案.
【自主解答】因为∠1=∠2=40°,所以a∥b,所以∠5=∠3=116°30',所以∠4=180°-∠5=63°30'.答案:63°30'
【总结提升】平行线的性质与判定的区别与联系1.区别:(1)性质:根据两条直线平行,证角相等或互补.(2)判定:根据两角相等或互补,证两条直线平行.2.联系:它们都是以两条直线被第三条直线所截为前提;它们的条件和结论是互逆的.3.总结:已知平行用性质,要证平行用判定.
题组一:平行线的判定1.(2013·铜仁中考)如图,在下列条件中,能判断AD∥BC的是(　　)A.∠DAC=∠BCAB.∠DCB+∠ABC=180°C.∠ABD=∠BDCD.∠BAC=∠ACD
【解析】选A.A、因为∠DAC=∠BCA,所以AD∥BC(内错角相等,两直线平行).故本选项正确;B、根据“∠DCB+∠ABC=180°”只能判定“DC∥AB”,而非AD∥BC.故本选项错误;C、根据“∠ABD=∠BDC”只能判定“DC∥AB”,而非AD∥BC.故本选项错误;D、根据“∠BAC=∠ACD”只能判定“DC∥AB”,而非AD∥BC.故本选项错误.
2.如图,直线a,b都与c相交,由下列条件能推出a∥b的是(　　)①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°.A.① B.①②C.①②③ D.①②③④
【解析】选D.因为∠1与∠2是同位角,∠3与∠6是内错角,所以①,②可推出a∥b;又因为∠1=∠7,∠1=∠8,所以∠7=∠8,而∠7与∠8是同位角,所以③也可以推出a∥b;因为∠5+∠7=180°,∠6+∠8=180°,又∠5+∠8=180°,所以∠6+∠7=180°,而∠6与∠7是同旁内角,故④也可以推出a∥b.
3.如图,以下条件能判定GE∥CH的是(　　)A.∠FEB=∠ECD B.∠AEG=∠DCHC.∠GEC=∠HCF D.∠HCE=∠AEG【解析】选C.∠GEC=∠HCF正确,因为它们是GE,CH被CF截得的内错角.
4.如图,直线EF分别交CD,AB于点M,N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是(　　)A.∠A=∠C B.∠E=∠FC.AE∥FC D.AB∥DC【解析】选D.因为∠EMD=65°,∠MNB=115°,所以∠CMN=∠EMD=65°,所以∠CMN+∠MNB=180°,所以AB∥DC.
5.如图所示,已知直线BF,CD相交于点O,∠D=40°,下面判定两条直线平行正确的是(　　)A.当∠C=40°时,AB∥CDB.当∠A=40°时,AC∥DEC.当∠E=120°时,CD∥EFD.当∠BOC=140°时,BF∥DE
【解析】选D.A项错误,因为∠C=∠D,所以AC∥DE;B项错误,不符合三线八角构不成平行;C项错误,因为∠E+∠D≠180°,所以CD不平行于EF;D项正确,因为∠DOF=∠BOC=140°,所以∠DOF+∠D=180°,所以BF∥DE.
6.如图,已知∠1=∠2,则图中互相平行的直线是　　　　.【解析】因为∠1=∠2,所以AD∥BC.答案:AD与BC
7.如图,直线AB过点C,∠2=80°,∠D=50°,∠1=∠3,AB∥DE吗?为什么?【解析】AB∥DE.因为∠2=80°,∠1=∠3(已知),∠1+∠2+∠3=180°(平角定义),所以∠1=∠3=50°,又因为∠D=50°(已知),所以∠1=∠D(等量代换),所以AB∥DE(内错角相等,两直线平行).
题组二:平行线的性质与判定的综合应用1.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是(　　)A.先向左转130°,再向左转50°B.先向左转50°,再向右转50°C.先向左转50°,再向右转40°D.先向左转50°,再向左转40°
【解析】选B.先向左转x°,再向右转y°形成的两个角是同位角关系,因为两次拐弯后,仍在原来的方向平行行驶,即两直线平行,所以x°=y°.
2.(2013·孝感中考)如图,∠1=∠2,∠3=40°,则∠4等于(　　)A.120°　　　B.130°　　　C.140°　　　D.40°【解析】选C.如图,因为∠1=∠2,所以a∥b,所以∠5=∠3=40°,所以∠4=180°-∠5=140°.
3.如图,直线EF分别与直线AB,CD相交于点G,H,已知∠1=∠2=50°,GM平分∠HGB交直线CD于点M.则∠3=(　　)A.60° B.65° C.70° D.130°【解析】选B.因为∠1=50°,所以∠BGH=180°-50°=130°,因为GM平分∠HGB,所以∠BGM=65°,因为∠1=∠2,所以AB∥CD(同位角相等,两直线平行),所以∠3=∠BGM=65°(两直线平行,内错角相等).
4.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?　　　　(填“合格”或“不合格”).【解析】因为∠ABC=120°,∠BCD=60°,所以∠ABC+∠BCD=180°,所以AB∥CD(同旁内角互补,两直线平行),所以这个零件合格.答案:合格
5.如图所示,修高速公路需要开山洞,为省时高效需在山的两面A,B同时开工,在A处测得洞的走向是南偏西68°12',那么在B处按　　　　方向开工,才能使山洞准确接通.【解析】在点B处建立方位图,只有保证内错角相等,即在B处按北偏东68°12'方向开工,才能使山洞准确接通.答案:北偏东68°12'
6.如图,要修一条乡村路与公路相接,修完后,检测人员测出∠1=70°,∠2=110°,就说新修路的两边是平行的.他说的对吗?为什么?【解析】对.理由:因为∠1=70°,所以∠1的邻补角等于110°,又∠2=110°,由“同位角相等,两直线平行”可知新修路的两边是平行的.
7.小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°,∠AED=70°.小明发现工人师傅只是量出∠BAE=30°,∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道什么原因吗?
【解析】如图,在∠AED的内部画∠AEF=∠BAE,则EF∥AB.又因为∠BAE=30°,∠AED=70°,所以∠DEF=40°,又∠EDC=40°,所以∠DEF=∠EDC,所以EF∥CD,根据如果两条直线都和第三条直线平行,那么这两条直线平行,得AB∥CD.