初中数学湘教版八年级下册2.1 多边形教学设计

第二章  四边形

2．1 多边形的内角和与外角和(1)

重点、难点

重点：多边形的概念，四边形和多边形的内角和  

难点：多边形内角和公式的推到过程。

教学过程

一 创设情境，导入新课

1 三角形的内角和等于多少？（180）

2 四边形的内角和等于多少呢？为什么？

四边形的内角和等于360º，理由是：

连结AC，则四边形ABCD被分成了两个三角形，因此四边形的内角和等于一个三角形的内角和的2倍。即：2×180º=360º       由此得到:四边形的内角和等于360º

2观察下面图形，你能抽象出什么样的几何图形呢？

在日常生活中我们经常会见到五边形、六边形、八边形等等。今天我们学习-----2．1 多边形的内角和与外交和(1)（板书课题）

二 合作交流，探究新知

1 请你说一说什么叫多边形？

   在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形。组成多边形的各条线段叫多边形的边，每相邻两条边的公共端点叫多边形的顶点，连结不相邻两个顶点的线段叫做多边形的对角线，相邻两边组成的角叫多边形的内角。简称多边形的角。

   说明：我们的课本今后说的多边形都是凸多边形，即：多边形总在一条边所在的直线的同旁。

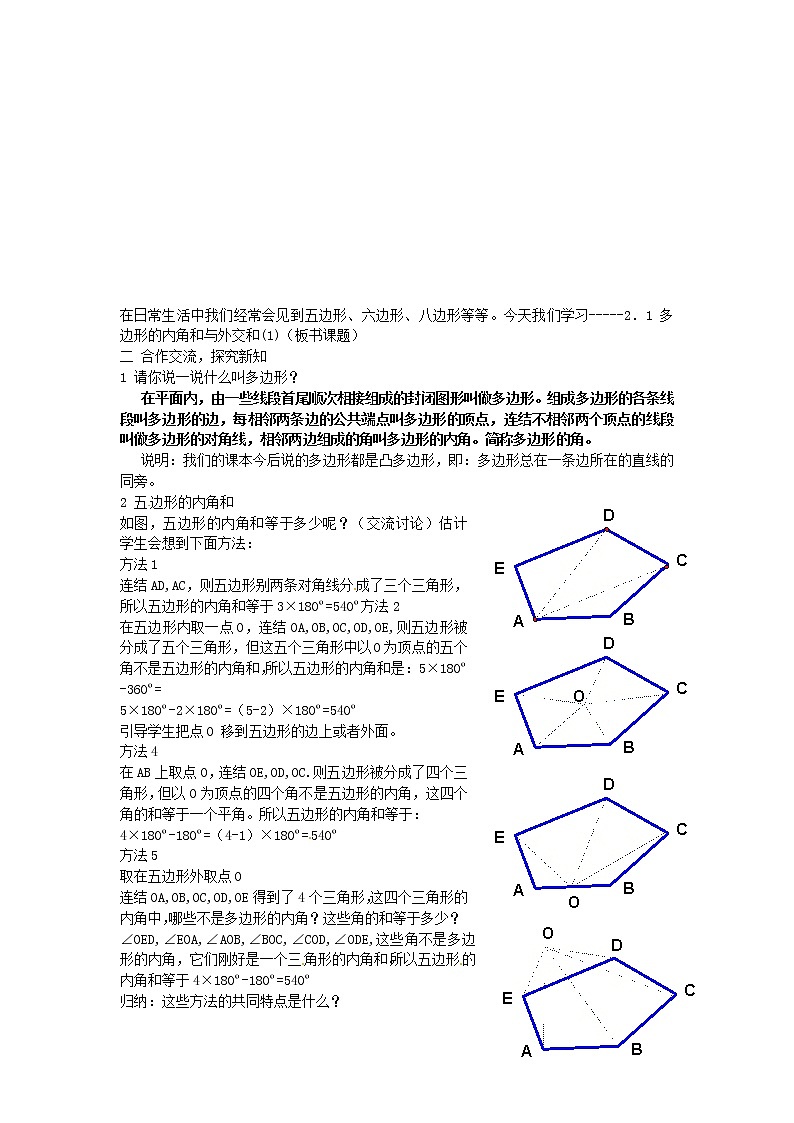
2 五边形的内角和

如图，五边形的内角和等于多少呢？（交流讨论）估计学生会想到下面方法：

方法1

连结AD,AC，则五边形别两条对角线分成了三个三角形，所以五边形的内角和等于3×180º=540º方法2

在五边形内取一点O，连结OA,OB,OC,OD,OE,则五边形被分成了五个三角形，但这五个三角形中以O为顶点的五个角不是五边形的内角和，所以五边形的内角和是：5×180º-360º=

5×180º-2×180º=（5-2）×180º=540º

引导学生把点O 移到五边形的边上或者外面。

方法4

在AB上取点O，连结OE,OD,OC.则五边形被分成了四个三角形，但以O为顶点的四个角不是五边形的内角，这四个角的和等于一个平角。所以五边形的内角和等于：

4×180º-180º=（4-1）×180º=540º

方法5

取在五边形外取点O

连结OA,OB,OC,OD,OE得到了4个三角形，这四个三角形的内角中，哪些不是多边形的内角？这些角的和等于多少？

∠OED,∠EOA,∠AOB,∠BOC,∠COD,∠ODE,这些角不是多边形的内角，它们刚好是一个三角形的内角和。所以五边形的内角和等于4×180º-180º=540º

归纳：这些方法的共同特点是什么？

取点O,将点O与五边形的各个顶点连结起来构成三角形，把多边形的内角和转化成三角形的内角和。

3 多边形的内角和

根据方法2，(在多边形内取点O , 把点O与多边形 各个顶点连结)请你填写下表

归纳：n边形的内角和等于（n-2）×180º

三 应用迁移，巩固提高

例1 如图，把△ABC的纸片沿着DE折叠，当点A落在四边形BCED内部时，则∠A与

∠1+∠2之间有一种数量关系始终保持不变，请找以找这个规律，你发现的规律是（   ）

A ∠A=∠1+∠2,  B 2∠A=∠1+∠2,  C 3∠A=2∠1+∠2,  D 3∠A=2(∠1+∠2)

解：∵∠ADE=,∠AED=

∴∠A=180º-(∠ADE+∠AED)=180º--

    =(∠1+∠2)

例2 （1）十边形的内角和等于______.

(2) 如果十边形的每一个内角都相等，那么每一个内角等于____.

三 课堂练习，巩固提高   P 36    1, 2

补充：

1 一个多边形的内角和不可能是(  )     A 560º  B   1080º   C  720º   D  1800º

2 一个多边形的内角和是2340º，这个多边形是____边形。

3 一个多边形的边数增加1，内角和增加多少呢？