初中数学湘教版九年级下册1.5 二次函数的应用示范课ppt课件

这是一份初中数学湘教版九年级下册1.5 二次函数的应用示范课ppt课件，共10页。PPT课件主要包含了你能想出办法来吗，这是什么样的函数呢，如何确定a是多少，A18y等内容，欢迎下载使用。
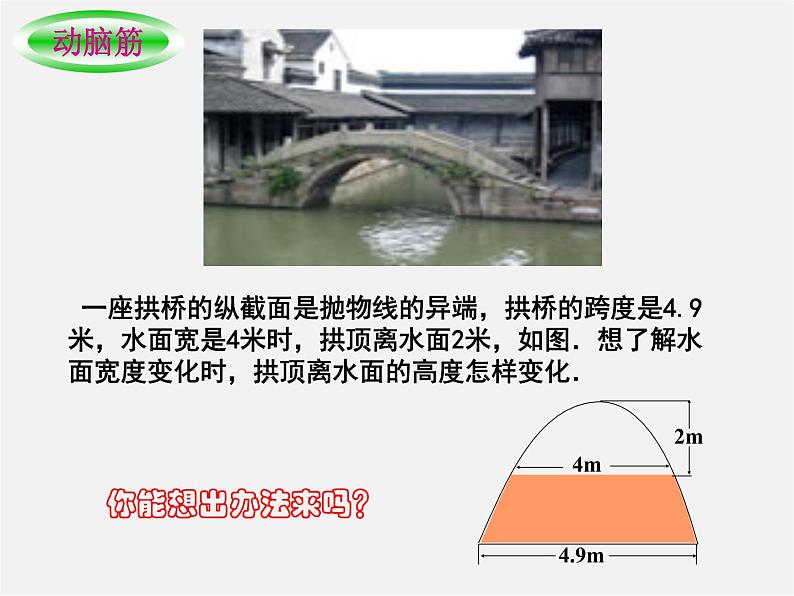
一座拱桥的纵截面是抛物线的异端，拱桥的跨度是4.9米，水面宽是4米时，拱顶离水面2米，如图．想了解水面宽度变化时，拱顶离水面的高度怎样变化．
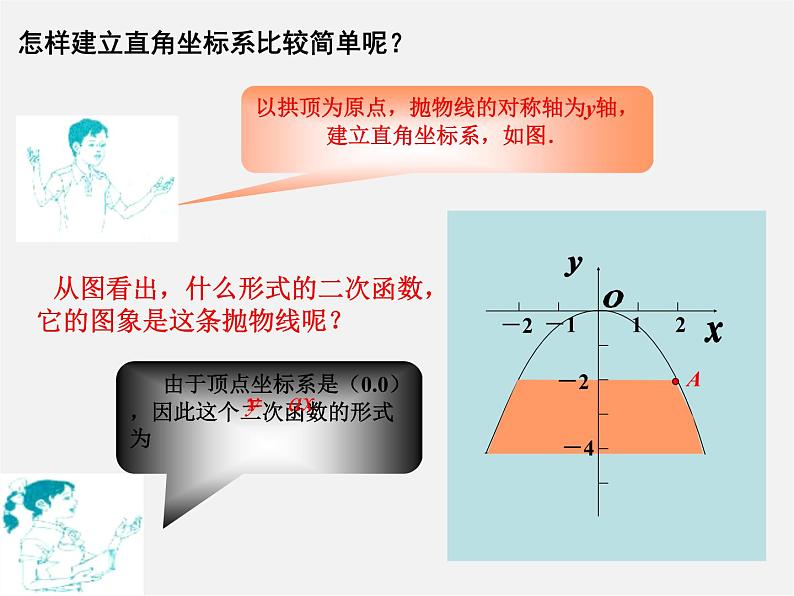
怎样建立直角坐标系比较简单呢？
以拱顶为原点，抛物线的对称轴为y轴，建立直角坐标系，如图．
从图看出，什么形式的二次函数，它的图象是这条抛物线呢？
由于拱桥的跨度为4.9米，因此自变量x的取值范围是：
你是否体会到：从实际问题建立起函数模型，对于解决问题是有效的？
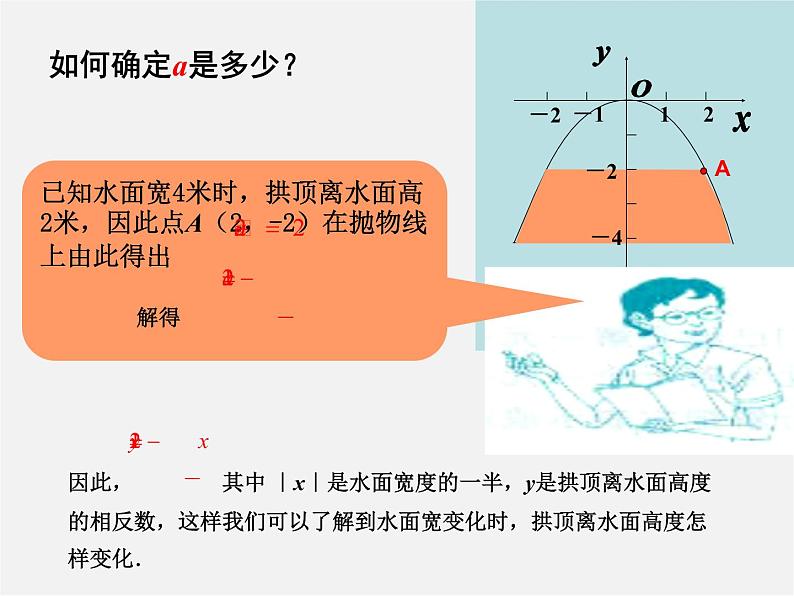
现在你能求出水面宽3米时，拱顶离水面高多少米吗？
某厂生产两种产品，价格分别为P1＝4万元/吨，P2＝8万元/吨；第一种产品的产量为Q1（吨），第二种产品的产量为1吨，成本函数为；
（1）当Q1=1吨时，成本C是多少？（2）求利润L与Q1的函数关系式？（3）当Q1=0.8吨时，利润L是多少？（4）当Q1=1吨时，利润L是多少？
1.在拱桥的例子中，当水面宽3.6m时，拱顶离水面高多少米？
由不节例题知，所对应的抛物线为
当水面宽3.6m时，如图A（1.8，y）
拱顶离水面的高度为 y =|－1.62|=1.62米
拱顶离水面高1.62米