湘教版九年级下册2.3 垂径定理课堂教学课件ppt

这是一份湘教版九年级下册2.3 垂径定理课堂教学课件ppt，共39页。PPT课件主要包含了如图理由是，不是直径，方法归纳，知识延伸等内容，欢迎下载使用。

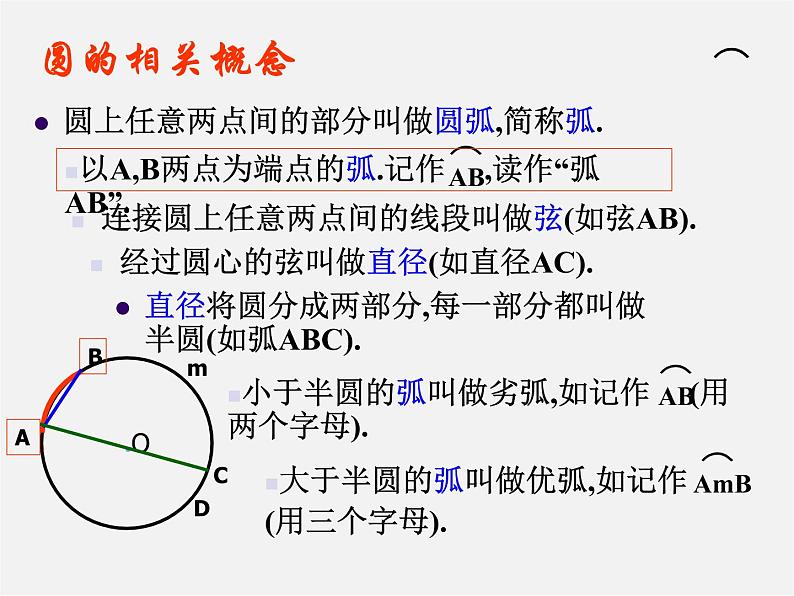
圆上任意两点间的部分叫做圆弧,简称弧.
直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).
连接圆上任意两点间的线段叫做弦(如弦AB).
经过圆心的弦叫做直径(如直径AC).
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
可利用折叠的方法即可解决上述问题.
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
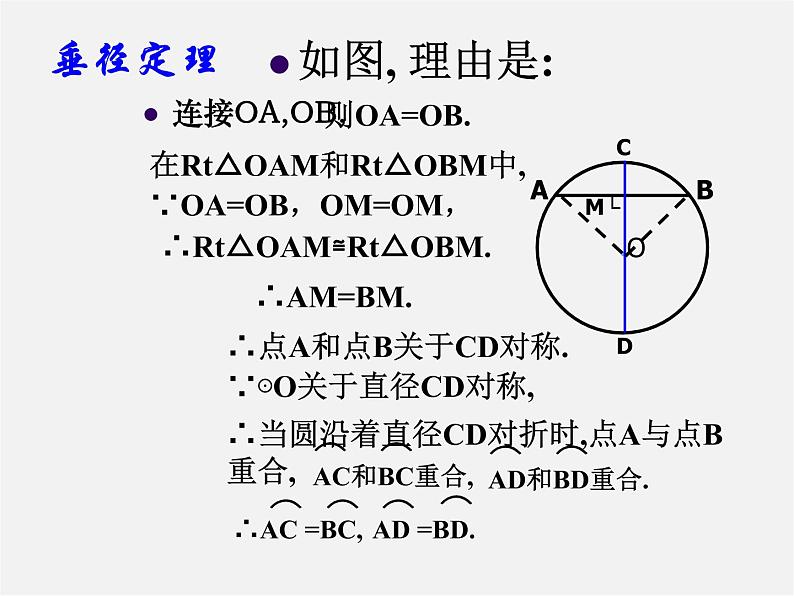
如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．（1）圆是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有那些相等的线段和弧？为什么？
（1）是轴对称图形．直径CD所在的直线是它的对称轴
（2） 线段： AE=BE
弧:AC=BC,AD=BD
把圆沿着直径CD折叠时，CD两侧的两个半圆重合，点A与点B重合，AE与BE重合，AC , AD分别与BC 、BD重合．
即直径CD垂直于弦AB，平分弦AB,并且平分AB及ACB
垂径定理： 垂直于弦的直径平分弦，并且平分弦所对的两条弧．
在Rt△OAM和Rt△OBM中,
∵OA=OB，OM=OM，
∴Rt△OAM≌Rt△OBM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
在下列图形，符合垂径定理的条件吗？
平分弦 的直径垂直于弦，并且平分弦所对的两条弧．
AB是⊙O的一条弦,且AM=BM.
你能发现图中有哪些等量关系?与同伴说说你的想法和理由.
右图是轴对称图形吗?如果是,其对称轴是什么?
平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧.
“知二推三” (1)垂直于弦 (2)过圆心 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧注意:当具备了(1)(3)时,应对另一 条弦增加”不是直径”的限制.
例1 如图，已知在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径。
变式： 如图，已知在⊙O中，弦AB的长为8cm，CD是⊙O的直径，CD⊥ＡB垂足为E，DE＝2cm,求⊙O的半径。
1．半径为4cm的⊙O中，弦AB=4cm, 那么圆心O到弦AB的距离是 。2．⊙O的直径为10cm，圆心O到弦AB的 距离为3cm，则弦AB的长是 。3．半径为2cm的圆中，过半径中点且 垂直于这条半径的弦长是 。
1.如图,在⊙O中,弦AB的长为8cm,圆心到AB的距离为3cm,则⊙O的半径为 .
2.弓形的弦长AB为24cm，弓形的高CD为8cm，则这弓形所在圆的半径为　　　　.
1.垂径定理经常和勾股定理结合使用。2.解决有关弦的问题时，经常（1）连结半径；（2）过圆心作一条与弦垂直的线段等辅助线，为应用垂径定理创造条件。
例1：赵州桥的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4米，拱高（弧的中点到弦的距离）为7.2米，你能求出赵州桥主桥拱的半径吗？
练习：在⊙Ｏ中，ＡＢ、AC为互相垂直且相等的两条弦，ＯＤ⊥ＡＢ于Ｄ，ＯＥ⊥ＡＣ于Ｅ．求证：四边形ＡＤＯＥ是正方形．
如果圆的两条弦互相平行，那么这两条弦所夹的弧相等吗？
圆的两条平行弦所夹的弧相等
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?
老师提示: 这两条弦在圆中位置有两种情况:
垂径定理的推论 圆的两条平行弦所夹的弧相等.
1.在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
2、如图4，在⊙O中，AB为⊙O的弦，C、D是直线AB上两点，且AC＝BD求证：△OCD为等腰三角形。
3、如图，两个圆都以点O为圆心，小圆的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系？为什么？
已知:⊙O中弦AB∥CD且AB=9cm,CD=12cm, ⊙O的直径为15cm,则弦AB,CD间的距离为( ) ; 或10.5cm D.都不对;
解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件。
常用辅助线:垂直于弦的直径
请围绕以下两个方面小结本节课：1、从知识上学习了什么？２、从方法上学习了什么？
圆的轴对称性；垂径定理及其推论
（１）垂径定理和勾股定理结合。（２）在圆中解决与弦有关的问题时常作的辅助线 ——过圆心作垂直于弦的线段； ——连接半径。
6.已知点P是半径为5的⊙O内的一定点，且OP=4，则过P点的所有弦中，弦长可能取的整数值为（ ）
A.5，4，3 B.10，9，8，7，6，5，4，3 C.10，9，8，7，6 D.10，9，8
12.已知直径AB被弦CD分成AE=4,EB=8,CD和AB成300角,则弦CD的弦心距OF=____;CD=_____.
在a,d,r,h中，已知其中任意两个量,可以求出其它两个量.
13.已知：如图，直径CD⊥AB，垂足为E .⑴若半径R = 2 ，AB = , 求OE、DE 的长. ⑵若半径R = 2 ，OE = 1 ，求AB、DE 的长.⑶由⑴ 、⑵两题的启发，你还能编出什么其他问题？
已知：AB和CD是⊙O内的两条平行弦，，AB=6cm，CD=8cm，⊙O的半径为5cm，
（1）请根据题意画出符合条件的图形
（2）求出AB、与CD间的距离。
1、判断： ⑴垂直于弦的直线平分这条弦,并且平分弦所对 的两条弧. （ ）⑵平分弦所对的一条弧的直径一定平分这条弦所 对的另一条弧. （ ）⑶经过弦的中点的直径一定垂直于弦. （ ）⑷圆的两条弦所夹的弧相等，则这两条弦平行. ⑸弦的垂直平分线一定平分这条弦所对的弧. （ ）
3、已知：如图，⊙O 中， AB为 弦，C 为 弧AB 的中点，OC交AB 于D ，AB = 6cm ，CD = 1cm. 求⊙O 的半径OA.
4、如图为一圆弧形拱桥，半径OA = 10m，　　拱高为4m，求拱桥跨度AB的长。
4.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.