湘教版九年级下册2.1 圆的对称性课文内容ppt课件

这是一份湘教版九年级下册2.1 圆的对称性课文内容ppt课件，共27页。PPT课件主要包含了图片欣赏，学前回顾，导入新知，实验探究一，探索发现，实验探究二，深入理解，CD过圆心，CD⊥AB于E，AEBE等内容，欢迎下载使用。
下列哪些图形是轴对称图形，若是轴对称图形，有几条对称轴？
问题2：圆如果是轴对称图形，它的对称轴有几条？
问题1：圆是轴对称图形吗？
拿出准备好的的圆，任意作一条直径AB, 然后沿着直径所在的直线把纸折叠,你发现了什么?再长任意作一条直径CD，重复以上的操作，还有同样的结论吗？
圆是轴对称图形，每一条直径所在的直线都是对称轴。
判断：任意一条直径都是圆的对称轴（ ）
（1）圆的对称轴是直线，不能说每一条直径都是圆的对称轴;
（2）圆的对称轴有无数条．
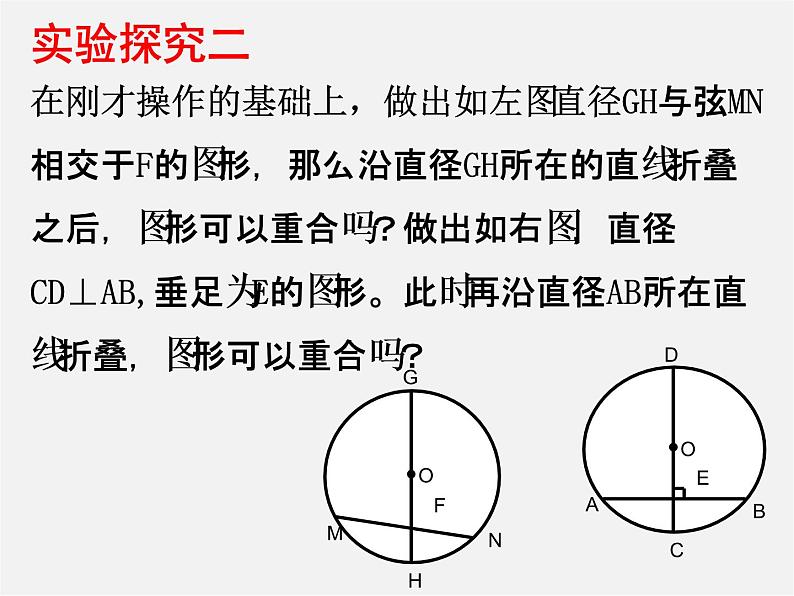
在刚才操作的基础上，做出如左图直径GH与弦MN相交于F的图形，那么沿直径GH所在的直线折叠之后，图形可以重合吗？做出如右图，直径CD⊥AB,垂足为E的图形。此时再沿直径AB所在直线折叠，图形可以重合吗？
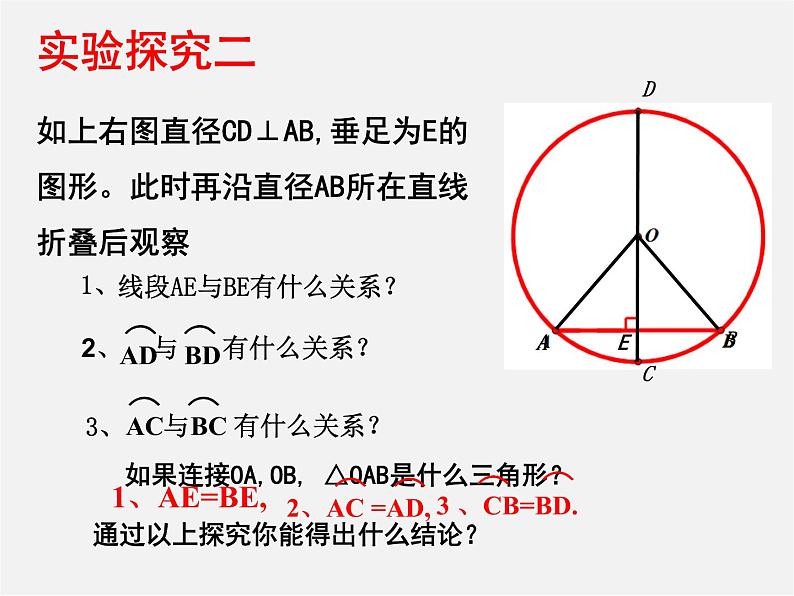
如上右图直径CD⊥AB,垂足为E的图形。此时再沿直径AB所在直线折叠后观察
通过以上探究你能得出什么结论？
如果连接OA,OB, △OAB是什么三角形？
垂径定理: 垂直于弦的直径平分弦以及弦所对的两条弧.
老师提示:垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
看下列图形，是否能使用垂径定理？
垂径定理的几个基本图形：
1、如图，AB是⊙O的直径，CD为弦，CD⊥AB于E，则下列结论中不成立的是（ ）
2、如图，O是⊙O的圆心，CD为弦，OE⊥CD于E，若CD=8则CE=––=––。
分析：构造垂径定理基本图形，那就想到过点O做AB的垂线，垂足为E，根据垂径定理得CE=DE,又AC=BD.所以AE=BE又因OE⊥AB所以OE垂直平分AB。从而得到OA=OB
证明：作OE⊥AB，垂足为E由垂径定理，得CE=DE，又因AC=BD所以AC+CE=BD+DE，即AE=BE所以OE垂直平分AB所以OA=OB
温馨提示：在解决与圆有关问题经常作的辅助线-------过圆心做弦的垂线构造垂径定理基本图形。
已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C、D两点.求证:AC=BD.
证明：作OE⊥AB，垂足为E由垂径定理，得AE=BE，CE=DE所以AE-CE=BE-DE，即AC=BD
变式（2）：再添一个同心圆，如图则 AC___BD。变式（3）：隐去变式（1）中的大圆，得下图连接OA，OB，设OA=OB，则 AC___BD。变式（4）：隐去变式（1）中的小圆，得下图连接OC，OD，设OC=OD，则 AC___BD。
如图，已知在⊙O中，弦AB的长为8厘米，圆心O到AB的距离为3厘米，求⊙O的半径。
解：连结OA. 过O作OE⊥AB，垂足为E，则OE＝3厘米，AE＝BE。∵AB＝8厘米 ∴AE＝4厘米 在Rt △AOE中，根据勾股定理有OA＝5厘米 ∴⊙O的半径为5厘米
温馨提示：过圆心做弦的垂线，连半径。
如图在⊙O中，圆心O到弦AB的距离为3cm，⊙O的半径为5cm。求：弦AB的长为多少？
温馨提示：在解决圆有关的问题时，常常构造以半弦、半径、圆心到弦的垂线段为边的直角三角形，利用垂径定理和勾股定理相结合的方法来解决。
解：设拱桥的半径为R米
即：R2=18.512+(R-7.23)2解这个方程得：R≈27.3∴赵州石拱桥的半径约为27.3
∴CD=7.23,∴OD=OC-CD=R-7.23
在RT⊿ODA中，由勾股定理得，OA2=AD2+OD2
温馨提示：在解决圆有关的问题时，常常构造以半弦、半径、圆心到弦的距离为边的直角三角形，利用垂径定理和勾股定理相结合的方法来解决。
如图，⊙O是水平放置的输油管道的横截面，其直径为26cm，油面的宽度AB=24cm,求油的最大深度。
在直径为650mm的圆柱形油槽内装入一些油后，若油面宽AB = 600mm，求油的最大深度.
如图：P为⊙O内一点，你能用三角尺画⊙O的一条弦，使点P恰为AB的中点吗？说明理由。
3、垂径定理和勾股定理有机结合计算弦长、半径、圆心到弦的距等问题的方法，构造直角三角形 。
2、在解决与圆有关问题时经常作的辅助线——过圆心做弦的垂线。
1、垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧。