七年级（上）期末数学试卷4

这是一份七年级（上）期末数学试卷4，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1. −3的相反数是( )
A.B.C.D.

2. 下列说法正确的是（ ）
A.−1不是单项式B.2πr2的次数是3
C.的次数是3D.-的系数是−1

3. 下列计算正确的是（ ）
A.2b2−b2＝1B.2a2+3a3＝5a5
C.2a+3b＝5abD.4a2b+ba2＝5a2b

4. “在山区建设公路时，时常要打通一条隧道，就能缩短路程”，其中蕴含的数学道理是( )
A.两点确定一条直线B.直线比曲线短
C.两点之间，线段最短D.垂线段最短

5. 如果x＝2是方程x+a＝−1的解，那么a的值是（ ）
A.0B.2C.−2D.−6

6. 如图，三条直线相发开点O，若CO⊥AB，∠1＝55∘，则∠2等于（ ）

A.30∘B.35∘C.45∘D.55∘

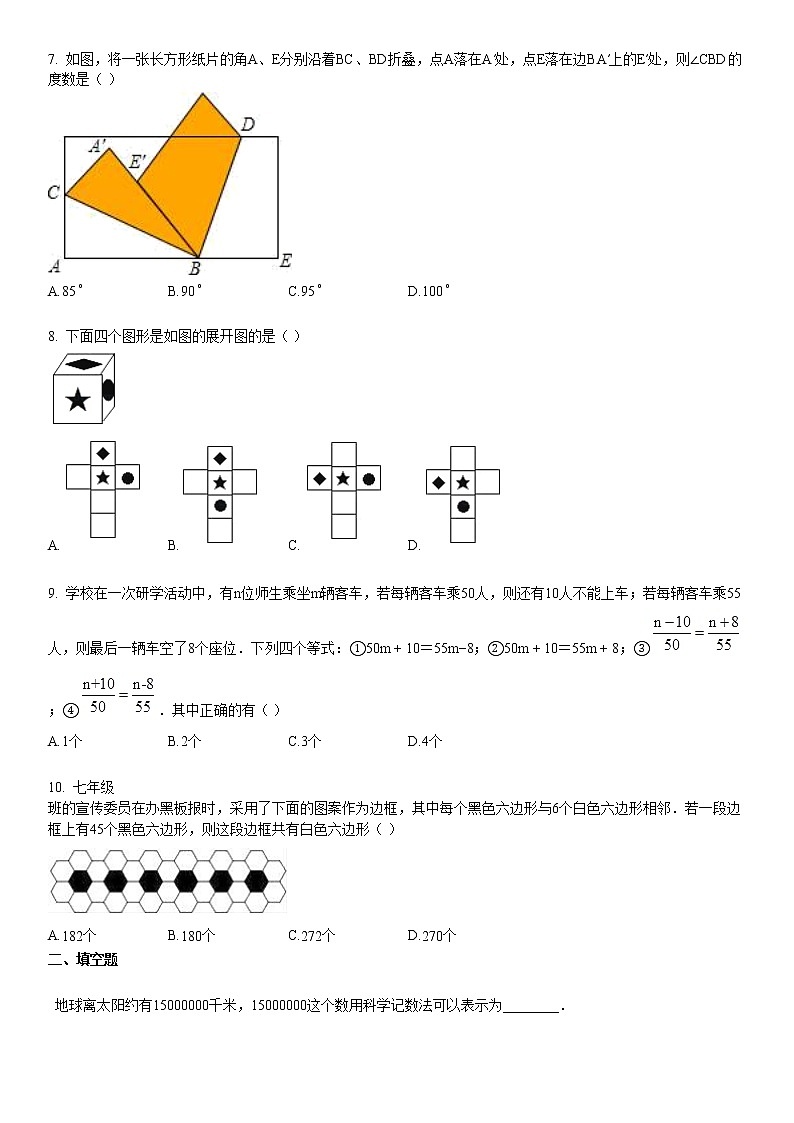
7. 如图，将一张长方形纸片的角A、E分别沿着BC、BD折叠，点A落在A′处，点E落在边BA′上的E′处，则∠CBD的度数是（ ）

A.85∘B.90∘C.95∘D.100∘

8. 下面四个图形是如图的展开图的是（ ）

A.B.C.D.

9. 学校在一次研学活动中，有n位师生乘坐m辆客车，若每辆客车乘50人，则还有10人不能上车；若每辆客车乘55人，则最后一辆车空了8个座位．下列四个等式：①50m+10＝55m−8；②50m+10＝55m+8；③；④．其中正确的有（ ）
A.1个B.2个C.3个D.4个

10. 七年级
班的宣传委员在办黑板报时，采用了下面的图案作为边框，其中每个黑色六边形与6个白色六边形相邻．若一段边框上有45个黑色六边形，则这段边框共有白色六边形（ ）

A.182个B.180个C.272个D.270个
二、填空题

地球离太阳约有15000000千米，15000000这个数用科学记数法可以表示为________．

互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为________元．

数a、b、c在数轴上对应点的位置如图所示，则|a+b|+|c+b|＝________．

某校在上午9：30开展“大课间”活动，上午9：30这一时刻钟面上分针与时针所夹的角等于_________度.

已知线段AB＝8cm，点C是线段AB所在直线上一点．下列说法：①若点C为线段AB的中点，则AC＝4cm；②若AC＝4cm，则点C为线段AB的中点；③AC>BC，则点C一定在线段AB的延长线上；④线段AC与BC的长度和一定不小于8cm，其中正确的有________（填写正确答案的序号）．

如图，有四个大小相同的小长方形和两个大小相同的大长方形按如图位置摆放，按照图中所示尺寸，则小长方形的长与宽的差是________．
三、解答题

请计算：


先化简，再求值：(4x2−2xy+y2)−3(x2−xy+y2)，其中x=−1，y=−.

平面上有四个点A、B、C、D，按照以下要求作图：
（1）作射线AD；

（2）作直线BC交射线AD于点K；

（3）连接AC、BD交于点P．

老师在黑板上出了一道解方程的题，小虎马上举手，要求到黑板上去做，他是这样做的：
5(3x−1)=2(4x+2)−1①，
15x−5=8x+4−1②，
15x−8x=4−1+5③
7x④，
x=⑤
老师说：小虎解一元一次方程的一般步骤都知道，但没有掌握好，因此解题出现了错误，请指出他的错步及错误原因： ，方程的正确的解是x＝ ．
然后，你自己细心的解下面的方程：.

如图，B、C两点把线段AD分成2:5:3的三部分，M为AD的中点，BM＝9cm，求CM和AD的长．

如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠2＝3∠1，∠COE＝70∘，求∠2的度数．

商场打折前，买1件A商品和1件B商品用了20元，买30件A商品和40件B商品用了680元．打折后，买100件A商品100件B商品用了1800元．请根据上述信息解决下列问题：
（1）打折前A、B两种商品的单价分别是多少？

（2）请在（1）的基础上提出一个能使题目剩余条件解决的问题，并加以解决．

定义一种新运算，观察下列式子：
1∗2=1×4+2=6，
2∗(−1)=2×4−1=7，
5∗3=5×4+3=23，
4∗(−2)=4×4−2=14，
（1）请你想一想：a∗b＝________．

（2）若a∗(−2b)＝6，请计算(a−b)∗(2a+b)的值．

已知，A，B在数轴上对应的数分别用a，b表示，且(12ab+100)2+|a−20|=0，P是数轴上的一个动点．

(1)在数轴上标出A，B的位置，并求出A，B之间的距离；

(2)已知线段OB上有点C且|BC|=6，当数轴上有点P满足PB=2PC时，求P点对应的数；

(3)动点P从原点开始第一次向左移动1个单位长度，第二次向右移动3个单位长度，第三次向左移动5个单位长度，第四次向右移动7个单位长度，…．点P能移动到与A或B重合的位置吗？若都不能，请直接回答．若能，请直接指出，第几次移动与哪一点重合．
参考答案与试题解析
2017-2018学年湖北省十堰市七年级（上）期末数学试卷
一、单选题
1.
【答案】
D
【考点】
相反数
绝对值
有理数大小比较
【解析】
相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，0的相反数还是0．
【解答】
根据相反数的定义可得：−3的相反数是3．故选D．
2.
【答案】
C
【考点】
单项式
【解析】
根据单项式的定义，多项式的次数，多项式的项，可得答案．
【解答】
解：A、−1是单项式，故此选项不符合题意；B、2πr2的次数是2；故此选项不符合题意；c、x23的次数是3；故此选项符合题意；D．−xz2的系数是−12
故选C．
3.
【答案】
D
【考点】
合并同类项
【解析】
根据合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变进行计算即可．
【解答】
解：A、2b2⋅b2=b2，故A错误；
B、2a2与3a3不是同类项，不能合并，故B错误；
C、2a与3b不是同类项，不能合并，故C错误；
D、4a2b+b2=5a2b，故D正确．
故选D．
4.
【答案】
C
【考点】
线段的性质：两点之间线段最短
【解析】
根据线段的性质解答即可．
【解答】
解：由线段的性质可知：
两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些所有的线中，线段最短．
故选C．
5.
【答案】
C
【考点】
方程的解
【解析】
将
【解答】
解：将x=2代入方程x=2代入12x+a=−1加加得． 得1+a=−1
解得：a=−2
故选：C．
6.
【答案】
B
【考点】
对顶角
【解析】
根据垂线的定义求出∠3，然后利用对顶角相等解答．
【解答】
解：CO⊥AB,∠1=55∘
∠3=90∘−∠1=90∘−55∘=35∘
∠2=∠3=35∘
故选B．
7.
【答案】
B
【考点】
翻折变换（折叠问题）
角的计算
平行线的性质
【解析】
试题解析：根据折叠的性质可得：∠ABC=∠ABC∠EBD=∠EBD,∵∠ABC+∠ABC+∠EBD+∠EBD=180∘∴2∠ABC+2∠EBD
=180∘∠ABC+∠EBD=90∘．2CBD=90∘．故选B．
【解答】
此题暂无解答
8.
【答案】
A
【考点】
几何体的展开图
生活中的平移现象
反比例函数图象上点的坐标特征
【解析】
由平面图形的折叠及正方体的展开图解题，注意带图案的三个面有一个公共顶点．
【解答】
A、能折叠成原正方体的形式，符合题意；
B、C带图案的三个面不相邻，没有一个公共顶点，不能折叠成原正方体的形式，不符合题意；
D、折叠后带方块的面在上面、带五角星的面在正面时，带圆的面在左边与原正方体中的位置不同，不符合题意，
故选A．
9.
【答案】
B
【考点】
由实际问题抽象出一元一次方程
整式的加减
列代数式
【解析】
首先要理解清楚题意，知道总的客车数量及总的人数不变，然后采用排除法进行分析从而得到正确答案．
【解答】
解：根据总人数列方程，应是50m+10=5m−8
根据客车数列方程，应该为：n−1050=n+855
所以正确的有①、③．
故选B．
10.
【答案】
A
【考点】
规律型：图形的变化类
平面镶嵌（密铺）
一元二次方程的应用
【解析】
根据图形分析可得：每增加一个黑色六边形，则需增加4个白色六边形，即可得若有n个黑色六边形，则共有6+4n−1个白色六
边形，由此代入计算得出答案即可．
【解答】
解：根据题意分析可得：每增加一个黑色六边形，则需增加4个白色六边形．若有n个黑色六边形，则共有6+4n−1个白色六边
形，若边框上有45个黑色六边形，则这段边框共有白色六边形6+4×45−1=182个．
故选A．
二、填空题
【答案】
15×7.
【考点】
科学记数法--表示较大的数
科学记数法--表示较小的数
科学记数法--原数
【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位
，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．
【解答】
解：将15000000用科学记数法表示为：1.5×107
故答案为：1.5×107
【答案】
80
【考点】
一元一次方程的应用——打折销售问题
一元一次方程的应用——工程进度问题
由实际问题抽象出一元一次方程
【解析】
设该商品的进价为x元，根据售价一进价=利润，即可得出关于x的一元一次方程，解之即可得出结论．详解：设该商品的进价为x元，根据题意得：
200×0.5−x=20
解得：x=80
故答案为80．
【解答】
此题暂无解答
【答案】
a−c
【考点】
有理数大小比较
绝对值
数轴
整式的加减
非负数的性质：绝对值
在数轴上表示实数
【解析】
试题解析：由数轴可知1c<0=a−c
【解答】
此题暂无解答
【答案】
105
【考点】
钟面角
【解析】
钟表12个数字，每相邻两个数字之间的夹角为30∘，钟表上9点30分，时针指向9，分针指向6，两者之间相隔3.5个数字．
【解答】
解：3×30∘+15∘=105∘．
∴ 钟面上9点30分时，分针与时针所成的角的度数是105度．
故答案为：105．
【答案】
①④
【考点】
两点间的距离
【解析】
①②根据中点的定义即可求解；③举反例即可求解；④点C在线段AB上是线段AC与BC的长度和最小为8cm；依此即可求解
【解答】
解：线段AB=8cm，点C是线段AB所在直线上一点，
∴ ．①若点C为线段AB的中点，则AC=4cm是正确的；
②若AC=4cm，则点C为线段AB的中点或在线段AB的反向延长线上，原来的说法是错误的；
③若AC>BC，则点C可能在线段AB上，原来的说法是错误的；
④线段AC与BC的长度和一定不小于8cm，是正确的．
故答案为①④．
【答案】
加加加a−b2
【考点】
规律型：图形的变化类
二元一次方程组的应用——几何问题
列代数式
【解析】
设小长方形的长为x，宽为y，根据题意求出x−y的值，即为长与宽的差．
【解答】
设小长方形的长为x，宽为y．
根据题意，得a+y=b−y+x，即2x−2y=a−b
整理得x−y=a−b2
则小长方形的长与宽的差是a−b2
三、解答题
【答案】
解：360×3+98
=1080+98
=1178（米）
答：是1078米。
【考点】
图文应用题
【解析】
根据图示可知，第二条线段比第一条线段的3倍还多98米，据此列式计算即可解答。
【解答】
解：360×3+98
=1080+98
=1178（米）
答：是1078米。
【答案】
x2+xy−2)？，1.
【考点】
整式的加减——化简求值
【解析】
原式去括号后合并同类项得到最简结果，将x与y的值代入计算即可求出值．
【解答】
解：原式=4x2−2xy+y2−3x2+3xy−3y2
=x2+xy−2y2
当x=−1,y=−12加,加式=1+12−12=1
故
【答案】
（1）详见解析；
（2）详见解析；
（3）详见解析.
【考点】
直线、射线、线段
【解析】
（1）直接利用射线的定义得出答案；
（2）根据直线的定义得出交点；
【解答】
（1）直接利用线段的定义得出答案.
解：（1）如图所示：AD即为所求；
（2）如图所示：点K即为所求；
（3）如图所示：点P即为所求.
【答案】
①去分母时右边−1没有乘以10；④等式右边缺失；⑤化系数为1时，没有除以x的系数；−17x=4
【考点】
解一元一次方程
【解析】
依据解一元一次方程的步骤：去分母、去括号、移项、合并同类项、系数化为1求解可得．
【解答】
他的错步及错误原因：①去分母时右边∼1没有乘以10；④等式右边缺失，⑤化系数为1时，没有除以x的系数；方程的正确的解
是x=−17
2x+1−4=8+2−x,2x+2−4=8+2−x,2x+x=8+2−2+4,3x=12,x=4
【答案】
CM=6cm,AD=30cm
【考点】
两点间的距离
【解析】
由已知B，C两点把线段AD分成2:5:3三部分，所以设AB=2xcm,BC=5xcm,CD=3xcm，根据已知分别用x表示出
AD，MD,从而得出BM，继而求出x，则求出CM和AD的长．
【解答】
解：设AB=22xm,BC=5,m,CD=33×m
所以AD=AB+BC+CD=10,ωcm
因为M是AD的中点
所以AM=MD=12AD=55cm
所以BM=AM−AB=5x−2x=3xm
因为BM=9cm
所以3x=9,x=3
故CM=MD−CD=5x−3x=2x=2×3=6cm
AD=10x=10×3=30cm
【答案】
I加加160∘
【考点】
角平分线的性质
【解析】
设∠DOE=x∘，把其它角用DOE表示，依据平角为180∘，找出角与角之间的关系，依据∠COE=70∘求解即可．
【解答】
设∠DOE=，则∴AOD=180∘−4∘
OC平分∠AOD
小∠3=12∠AOD=12180∘−4x0=90∘−2x2
△COE=70∘
90−2x+x=70
x=20
∠BOE=3×20∘=60∘
故∠BOE的度数为60∘.
【答案】
（1）打折前，A商品的单价是12元，B商品的单价是8元；
（2）打折后，买100件A商品和100件B商品比打折前节约200元．
【考点】
二元一次方程组的应用——销售问题
【解析】
（1）设打折前，A商品的单价是x元，B商品的单价是y元，根据买1件A商品和1件B商品用了20元，买30件A商品和40件B商品用了
680元．列方程组可求出x和y；
（2）答案不唯一．设问恰当，解答合理即可．
【解答】
（1）设打折前，A商品的单价是x元，B商品的单价是y元，依题意有
x+y=20,30x+40y=680
解得x=12y=8
答：打折前，A商品的单价是12元，B商品的单价是8元．
（2）答案不唯一．如：打折后，买100件A商品和100件B商品比打折前节约多少钱？
当x=12,y=8t时，100x+100y−1800=200
答：打折后，买100件A商品和100件B商品比打折前节约200元．
故答案为（1）打折前，A商品的单价是12元，B商品的单价是8元；（2）打折后，买100件A商品和100件B商品比打折前节约200元．
【答案】
（1）4a+b;
（2）9.
【考点】
有理数的混合运算
【解析】
（1）根据提供的信息，*的运算法则是*前面的数乘以4再加上运算符号后面的数，然后写出结果即可；
（2）先根据运算规则与已知条件求出a、b的关系，然后再根据运算规则计算a−bx2a+b并把a、b的关系代入整理后的算式计算
即可求解．
【解答】
（1）观察上式可得a′b=4a+b
（2）ax−2b=6
4a−2b=6
2a−b=3
a−bx2a+b=4a−b+2a+b
=4a−4b+2a+b
=6a−3b
=32a−b
=3×3
=9
故答案为（1）4a+b；（2）9．
【答案】
解：(1)∵ (12ab+100)2+|a−20|=0，
∴ 12ab+100=0，a−20=0，
∴ a=20，b=−10，
∴ AB=20−(−10)=30，
数轴上标出AB得：
(2)∵ |BC|=6且C在线段OB上，
∴ xC−(−10)=6，
∴ xC=−4，
∵ PB=2PC，
当P在点B左侧时PB当P在线段BC上时，
xP−xB=2(xc−xp)，
∴ xp+10=2(−4−xp)，
解得：xp=−6，
当P在点C右侧时，
xp−xB=2(xp−xc)，
xp+10=2xp+8，
xp=2，
综上所述P点对应的数为−6或2．
(3)第一次点P表示−1，第二次点P表示2，依次−3，4，−5，6…
则第n次为(−1)n⋅n，
点A表示20，则第20次P与A重合；
点B表示−10，点P与点B不重合．
【考点】
非负数的性质：偶次方
非负数的性质：绝对值
数轴
【解析】
(1)先根据非负数的性质求出a，b的值，在数轴上表示出A，B的位置，根据数轴上两点间的距离公式，求出A，B之间的距离即可；
(2)设P点对应的数为x，当P点满足PB=2PC时，分三种情况讨论，根据PB=2PC求出x的值即可；
(3)根据第一次点P表示−1，第二次点P表示2，点P表示的数依次为−3，4，−5，6…，找出规律即可得出结论．
【解答】
解：(1)∵ (12ab+100)2+|a−20|=0，
∴ 12ab+100=0，a−20=0，
∴ a=20，b=−10，
∴ AB=20−(−10)=30，
数轴上标出AB得：
(2)∵ |BC|=6且C在线段OB上，
∴ xC−(−10)=6，
∴ xC=−4，
∵ PB=2PC，
当P在点B左侧时PB当P在线段BC上时，
xP−xB=2(xc−xp)，
∴ xp+10=2(−4−xp)，
解得：xp=−6，
当P在点C右侧时，
xp−xB=2(xp−xc)，
xp+10=2xp+8，
xp=2，
综上所述P点对应的数为−6或2．
(3)第一次点P表示−1，第二次点P表示2，依次−3，4，−5，6…
则第n次为(−1)n⋅n，
点A表示20，则第20次P与A重合；
点B表示−10，点P与点B不重合．