2020-2021学年第二章 相交线与平行线综合与测试说课课件ppt

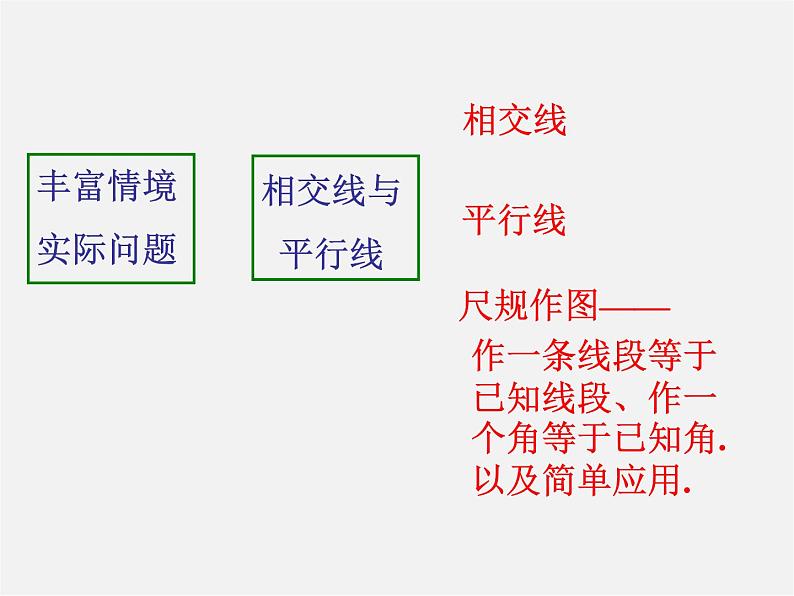
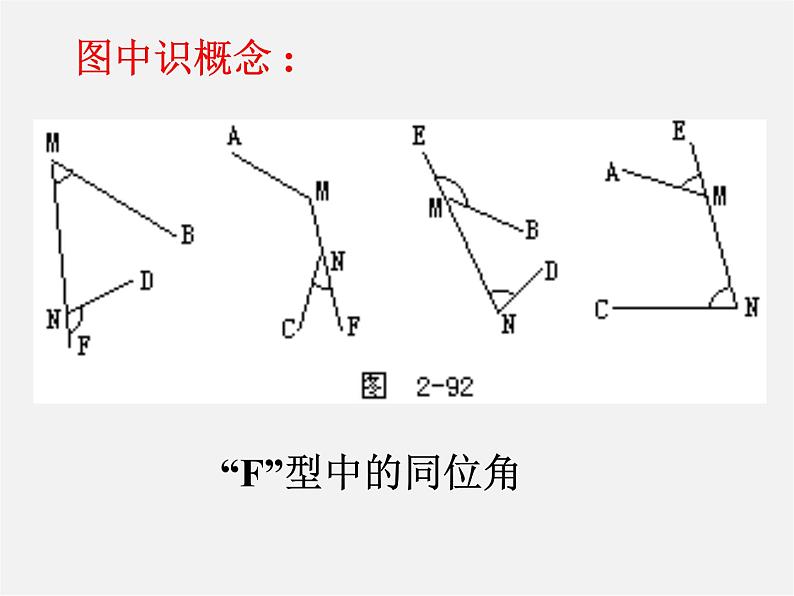
这是一份2020-2021学年第二章 相交线与平行线综合与测试说课课件ppt，共19页。PPT课件主要包含了相交线，对顶角，对顶角相等，平行线，探索直线平行的条件，探索直线平行的特征，图中识概念，“F”型中的同位角，1平行线定义，两直线平行的条件等内容，欢迎下载使用。
作一条线段等于已知线段、作一个角等于已知角.以及简单应用.
如果两个角的和是平角（或180°），称这两个角互为补角.
同角或等角的补角相等.
像上图中具有∠1与∠2这样位置关系的两个角就称它们互为邻补角.
注：互为补角只反映大小关系，不反映位置关系.而互为邻补角既反映大小关系，又反映位置关系.
如果两个角的和是直角（或90°），称这两个角互为余角.
同角或等角的余角相等.
注：互为余角只反映大小关系，不反映位置关系.
如图，直线AB与直线CD相交于点O，∠1与∠2有公共顶点O，它们的两边互为反向延长线，这样的两个角叫做对顶角.
注：对顶角既反映大小关系，又反映位置关系.
“Z”字型中的内错角
“U”字型中的同旁内角
（2）同位角相等，两直线平行.
（3）内错角相等，两直线平行.
（4）同旁内角互补，两直线平行.
（5）如果两条直线都和第三条直线平行，那么这 两条直线也平行.
注：同位角，内错角，同旁内角均不是平行线所特有的.它们只反映角的位置关系，而不反映大小关系.
（1）两直线平行，同位角相等.（2）两直线平行，内错角相等.（3）两直线平行，同旁内角互补.
（6）两条直线相交后，只有两对对顶角和一组邻补角，一组互余的角． （ ）
（1）下列说法中正确的是（ ）两条直线相交所成的角是对顶角.有公共顶点的角是对顶角.一个角的两个相邻补角是对顶角.有一边互为反向延长线，且相等的两个角是对顶角.
（2）如图1，如果AD∥BC,则有①∠A+∠B=180°②∠B+∠C=180° ③ ∠C+∠D=180°上述结论中正确的是（ ）只有①. B.只有②. C.只有③. D.只有①和③.
（3）如图2，如果l1 ∥l2 ,AB⊥l1 ，∠ABC=130°,那么∠α=（ ） A.60° B.50° C.40° D.30°.
3.如图3，（1）指出OA是什么方向的一条射线？ （2）画出OA的相反方向，并说出它的方位.
解：（1）OA是北偏东30°；
（2）OA的相反方向为南偏西30°.
4.如图4，HP平分∠EHD，∠1=55°，∠2=110°，直线AB、CD平行吗？请说明理由.
解：∵PH平分∠EHD，∠1=55°（已知）
∴∠GHP=∠1=55°（角平分线定义）
又∠2=110°（已知）
∴∠GHD=∠2（等量代换）
（同位角相等，两直线平行）
5.如图5，已知∠1=25°，∠B=65°，AB⊥AC.（1）AD与BC平行吗？请说明理由.（2）AB与CD平行吗？如果平行，请说明理由；如果不平行，应再增加什么条件？
解：∵ AB⊥AC （已知）
∴∠BAC=90°（垂直定义）
∴∠BCA=∠BAC-∠B=25°
∵ ∠B=65° （已知）
∴∠BCA=∠1(等量代换）
∵ ∠1=25°（已知）
∴AD∥BC(内错角相等，两直线平行）