七年级下册9.3 分式方程备课课件ppt

这是一份七年级下册9.3 分式方程备课课件ppt，共14页。PPT课件主要包含了相等关系是，以下是解题格式，风景区，速度时间，解得x15，-244x，审清题意，解这个分式方程等内容，欢迎下载使用。

列方程解应用题的一般步骤:
1、列分式方程、 解决现实情境中的问题。2、经历“实际问题—分式方程模型—求解—解释解的合理性”的过程，提高分析问题、解决问题的能力。
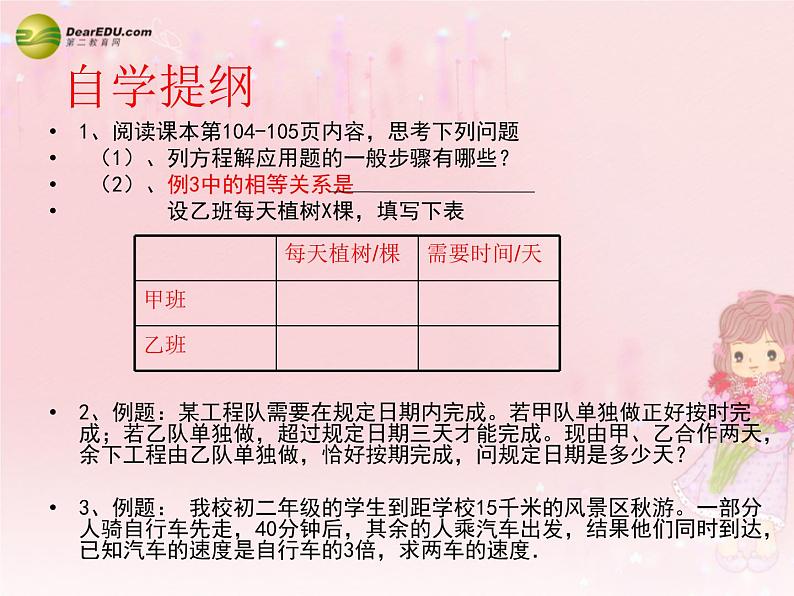
1、阅读课本第104-105页内容，思考下列问题 （1）、列方程解应用题的一般步骤有哪些？ （2）、例3中的相等关系是 设乙班每天植树X棵，填写下表2、例题：某工程队需要在规定日期内完成。若甲队单独做正好按时完成；若乙队单独做，超过规定日期三天才能完成。现由甲、乙合作两天，余下工程由乙队单独做，恰好按期完成，问规定日期是多少天？3、例题： 我校初二年级的学生到距学校15千米的风景区秋游。一部分人骑自行车先走，40分钟后，其余的人乘汽车出发，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度．
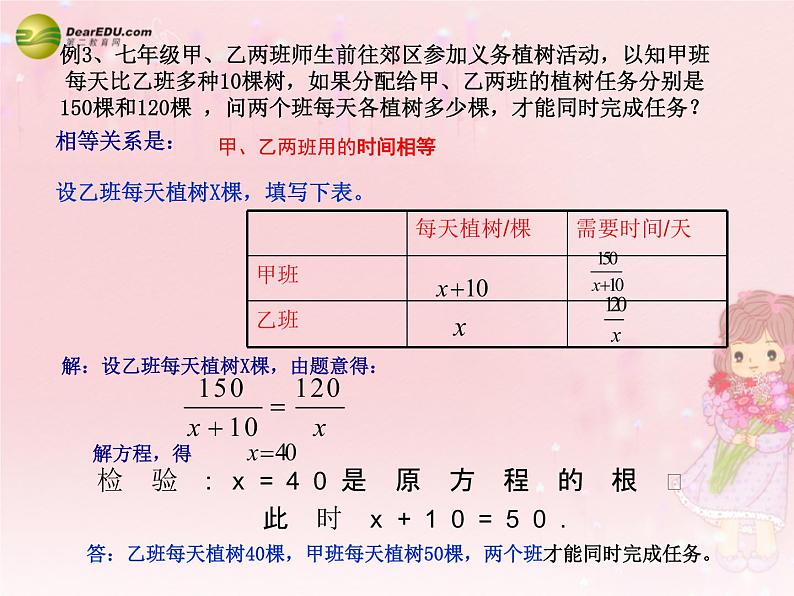
例3、七年级甲、乙两班师生前往郊区参加义务植树活动，以知甲班每天比乙班多种10棵树，如果分配给甲、乙两班的植树任务分别是150棵和120棵 ，问两个班每天各植树多少棵，才能同时完成任务？
甲、乙两班用的时间相等
设乙班每天植树X棵，填写下表。
解：设乙班每天植树X棵，由题意得：
答：乙班每天植树40棵，甲班每天植树50棵，两个班才能同时完成任务。
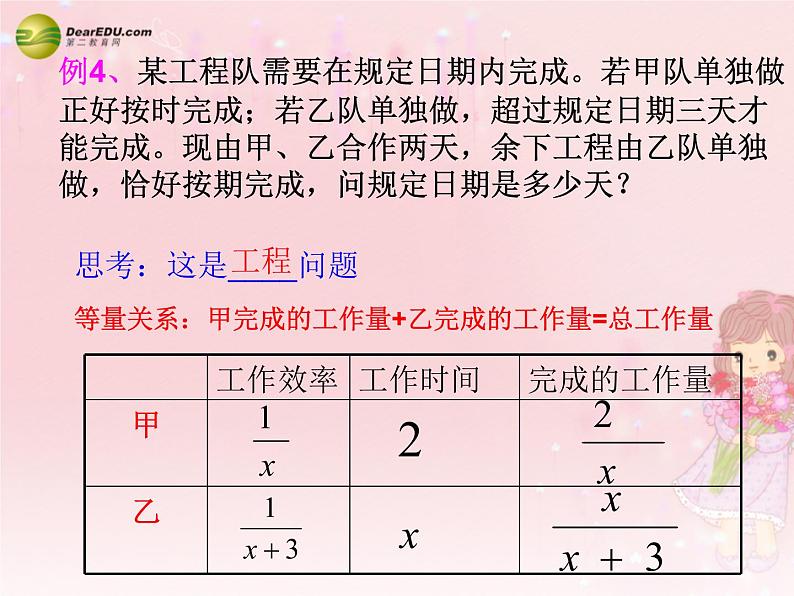
例4、某工程队需要在规定日期内完成。若甲队单独做正好按时完成；若乙队单独做，超过规定日期三天才能完成。现由甲、乙合作两天，余下工程由乙队单独做，恰好按期完成，问规定日期是多少天？
思考：这是____问题
等量关系：甲完成的工作量+乙完成的工作量=总工作量
等量关系：甲完成的工作量+乙完成的工作量=总做总量
设规定日期是x天，由题意，得
检验：当x=6时，x(x+3)≠0∴ x=6是原方程的根
在方程两边都乘以x(x+3)得:
2(x+3)+x=x(x+3)
例5、我校初二年级的学生到距学校15千米的风景区秋游，一部分人骑自行车先走，40分钟后，其余的人乘汽车出发，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度．
分析;设自行车的速度是x千米/时
自行车所用时间–汽车所用时间 =
例5、 我校初二年级的学生到距学校15千米的风景区秋游，一部分人骑自行车先走，40分钟后，其余的人乘汽车出发，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度．
解:设自行车的速度为x千米/时，那么汽车的速度为3x千米/时．依题意，得
解得 x = 15
经检验, 15是原方程的根
由 x = 15 得 3x=45
答:自行车的速度为15 千米/时，汽车的速度为45 千米/时．
练习二、甲、乙两人分别从相距目的地6千米和10千米的两地同时出发，甲、乙的速度比是3：4，结果甲比乙提前20分到达目的地。求甲、乙的速度。
思考：这是____问题，三个工作量为____________________
练习一、课本105页练习2 、3两题。
设甲的速度3x千米/时，则乙的速度是4x千米/时由题意得
答：甲的速度4.5千米/时，乙的速度是6千米/时。
∴ 3x=4.5 ，4x=6
检验：当x=1.5时，12x≠0∴ x=1.5是原方程的根
在方程两边都乘以12x得:
列分式方程解应用题的方法与步骤为：
——直接设未知数， 或间接设未知数
——根据等量关系列出分式方程
——既要验是否为所列分式方程的根，
又要验是否符合实际情况
——完整地写出答案，注意单位
列表法可以方便理解解应用题。列表是一种手段而不是目的，平常做应用题可在心中自有一张表格，逐项理清，而不必都要列在纸上。