






2021学年1.1.2集合间的基本关系图文课件ppt
展开观察下列各个集合,你能说出集合C与集合A,B之间的关系吗?
(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}
(2) A={x|x是有理数},B={x|x是无理数}, C={x|x是实数}.
集合C是由所有属于集合A和集合B的元素组成的.
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集,
即:A∪B__________________.记作A∪B(读作“A并B”),用Venn图表示为:
={x|x∈A,或x∈B}
A∪B={x |x ∈ A,或x ∈ B }
x∈A 或 x∈B包括三种情况:
(1)两个集合的并集中的元素就是将两个集合中的元素合在一起. ( )
(2)A∪B仍是一个集合,由所有属于集合A或属于集合B的元素组成. ( )
(3)若集合A和集合B有公共元素,根据集合元素的互异性,则在A∪B中仅出现一次. ( )
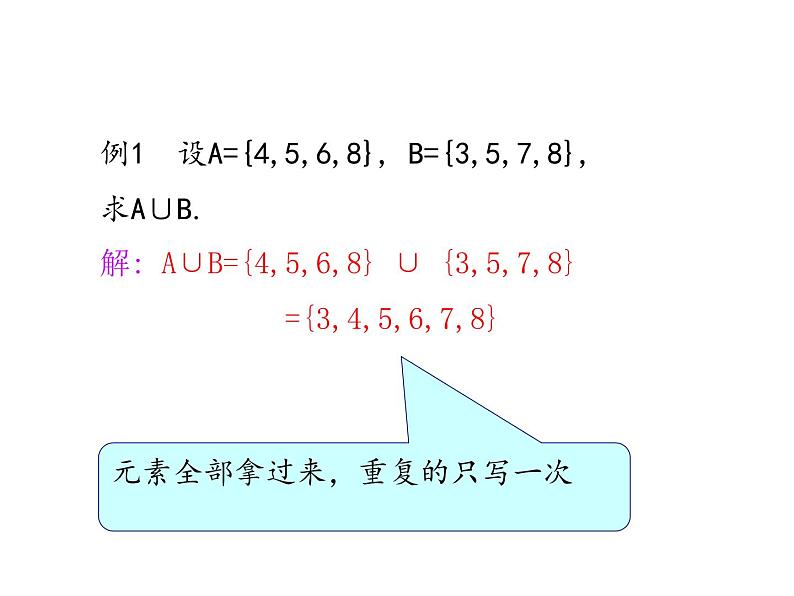
例1 设A={4,5,6,8}, B={3,5,7,8},求A∪B.
解: A∪B={4,5,6,8} ∪ {3,5,7,8} ={3,4,5,6,7,8}
元素全部拿过来,重复的只写一次
例2 设集合A={x∣-1<x<2},集合B={x∣1<x<3},求A∪B.
解:A∪B= {x∣-1<x<2}∪ {x∣1<x<3}
= {x∣-1<x< 3}
上述三组集合中,集合A,B与集合C的关系如何?你能用Venn图表示出它们之间的关系吗?
【解答】集合C中的元素既在集合A中,又在集合B中.各组集合均可用下图表示
由图形可以看出:集合C中的每一个元素既在集合A中,又在集合B中。
一般地,由所有属于A且属于B的元素组成的集合,称为集合A与B的交集,记作A∩B(读作“A交B”).
即A∩B={ x | x ∈A,且 x∈B}
例3 新华中学开运动会,设A={x︳x是新华中学高一年级参加百米赛跑的同学},B ={x︳x是新华中学高一年级参加跳高比赛的同学},求A∩B.
解:A∩B就是新华中学高一年级中那些既参加百米赛跑又参加跳高比赛的同学组成的集合.所以,A∩B={x︳x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}.
例4 设平面内直线l1上点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示l1,l2的位置关系.
解:平面内直线l1,l2可能有三种位置关系,即相交于一点,平行或重合.(1)直线l1,l2相交于一点P可表示为L1∩L2={点P};(2)直线l1 ,l2平行可表示为L1∩ L2= ;(3)直线l1 ,l2重合可表示为L1∩L2= L1=L2.
两个集合求交集,结果还是一个集合,由集合A与B的公共元素组成的集合,当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.
1.若集合M={x|-3<x≤5},N={x|x<-5,或x>5},则M∪N
2.设集合A={x|-1<x<a},B={x|1<x<3}且A∪B={x|-1<x<3},求a的取值范围.
人教B版 (2019)必修 第一册1.1.3 集合的基本运算教学课件ppt: 这是一份人教B版 (2019)必修 第一册1.1.3 集合的基本运算教学课件ppt,共13页。PPT课件主要包含了授课老师都乐,问题情境,发现问题和提出问题,猜想与假设,探究与论证,建构图式,自然语言,符号语言,深化概念,图形语言等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第一册1.1.3 集合的基本运算说课ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册1.1.3 集合的基本运算说课ppt课件,文件包含113《集合的基本运算》课件PPTpptx、113《集合的基本运算》第2课时教案docx等2份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
2020-2021学年1.1.3 集合的基本运算集体备课ppt课件: 这是一份2020-2021学年1.1.3 集合的基本运算集体备课ppt课件,文件包含113《集合的基本运算》第1课时课件PPTpptx、113《集合的基本运算》第1课时教案docx等2份课件配套教学资源,其中PPT共33页, 欢迎下载使用。













