高中数学人教版新课标A必修11.3.1单调性与最大(小)值背景图课件ppt

这是一份高中数学人教版新课标A必修11.3.1单调性与最大(小)值背景图课件ppt，共24页。PPT课件主要包含了创设情景，函数的最大值，构建数学，函数的最小值，想一想，归纳总结，题后反思，练一练等内容，欢迎下载使用。

前面我们学习了函数的单调性，知道了在函数定义域的某个区间上函数值的变化与自变量增大之间的关系，请大家看某市一天24小时内的气温变化图.
(1)说出气温随时间变化的特点.
从图象上看出0时4时之间气温下降,4时14时之间气温逐步上升,14时~24时气温逐渐下降.
(2)某市这一天何时的气温最高和何时的气温最低？
14时气温达到最高,4时气温达到最低.
(3)从图象上看出14时的气温为全天的最高气温,它表示在0~24时之间,气温于14时达到最大值,从图象上看出,图象在这一点的位置最高.这就是本节课我们要研究函数最大、最小值问题.
设函数y=f(x)的定义域为Ｉ,如果存在实数M满足:
(1)对于任意的xI,都有f(x)≤M;
(2)存在x0I,使得f(x0)=M.
则称M是函数y=f(x)的最大值(maximum value).
上面我们从直观的感受知道了最值的概念,下面给出严格的定义.
2.函数最大值应该是所有函数值中最大的,即对于任意的x∈I,都有f(x)≤M．
注意:1.函数最大值首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M；
定义中的两个条件缺一不可,只有(1)没有(2)不存在最大值点,而只有(2)没有(1),M不一定是函数y=f(x)的最大值. 比照最大值的定义, 最小值是如何定义的?
(1)对于任意的xI,都有f(x)≥M;
则称M是函数y=f(x)的最小值(minimum value).
函数的最大值从图象上看是在指定的区间里最高位置对应的点的纵坐标,好象有一种一览众山小的情景.同样函数的最小值从图象上看是在指定的区间里最低位置对应的点的纵坐标，好像有一种坐井观天的情景.
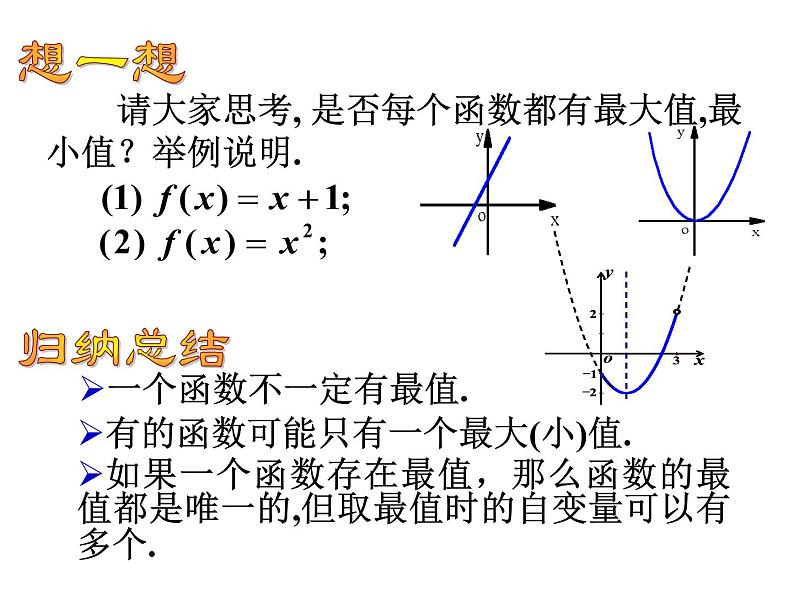
请大家思考, 是否每个函数都有最大值,最小值？举例说明.
一个函数不一定有最值.
有的函数可能只有一个最大(小)值.
如果一个函数存在最值，那么函数的最值都是唯一的,但取最值时的自变量可以有多个.
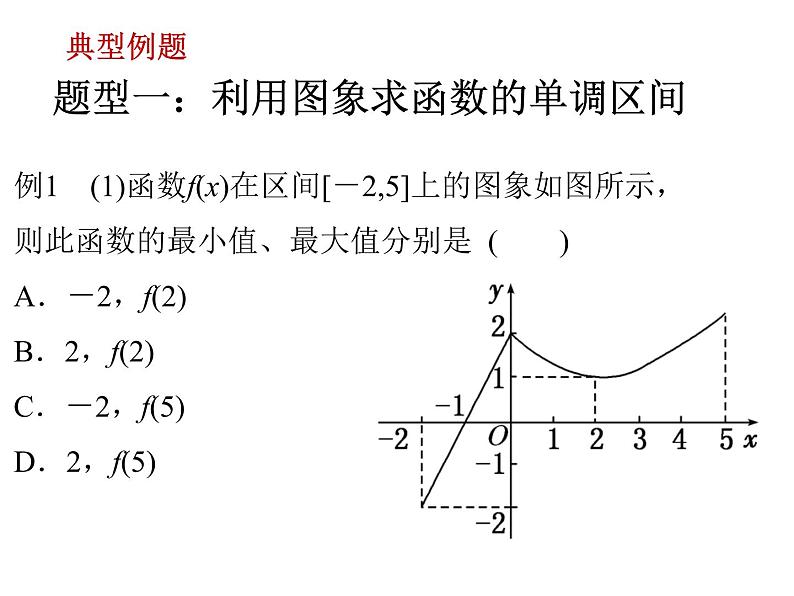
例1　(1)函数f(x)在区间[－2,5]上的图象如图所示，则此函数的最小值、最大值分别是 (　　)A．－2，f(2)B．2，f(2)C．－2，f(5)D．2，f(5)
题型一：利用图象求函数的单调区间
解：函数f(x)的图象如图
由图象可知f(x)的最小值为f(1)＝1，无最大值．
作出函数y＝|x－2|(x＋1)的图象，说明函数的单调性，并判断是否存在最大值和最小值．
题型二：二次函数的最值
答:烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.
(1)   x∈[0, 3](2)   x∈(2, 4](3)   x∈[-2, -1]
[思路探索]　借助二次函数的图象及单调性求解．
(1)   x∈[0, 3]，函数图象如图所示.
(2)   x∈(2, 4]时，函数单调递增，
所以x=4时，函数有最大值，且ymax=7，
函数值域为[2，7].
[例4](1)已知函数f(x)=x2-2x-3,若x∈[0,2],求函数f(x)的最值;(2)已知函数f(x)=x2-2x-3,若x∈[t,t+2],求函数f(x)的最值;(3)已知函数f(x)=x-2√x一3,求函数f(x)的最值.
(2)根据对称轴的位置情况讨论函数的单调性．
(1)确定二次函数图像的对称轴．
【规律总结】二次函数的最值通常借助图象，根据二次函数的性质求解，一般步骤：
题型三 ：利用单调性求函数的最值
【2】已知函数 求函数的最大值和最小值．
【3】在已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域__________.
规律总结：用单调性法求最值常用结论有：
(1)如果函数y＝f(x)在区间[a，b]上是增(减)函数，则在区间[a，b]的左、右端点处分别取得最小(大)值、最大(小)值．
（2)如果函数y＝f(x)在区间(a，b]上是增函数，在区间[b，c)上是减函数，则函数y＝f(x)，x∈(a，c)在x＝b处有最大值f(b)．　　
(3)如果函数y＝f(x)在区间(a，b]上是减函数，在区间[b，c)上是增函数，则函数y＝f(x)，x∈(a，c)在x＝b处有最小值f(b)．