沪科版八年级下册18.1 勾股定理课前预习ppt课件

这是一份沪科版八年级下册18.1 勾股定理课前预习ppt课件，共18页。PPT课件主要包含了勾股定理的应用，∵65666，引葭jiā赴岸，葭芦苇，旗杆有多高呢，x+1，风动红莲，数学来源于生活，服务于生活，试一试等内容，欢迎下载使用。

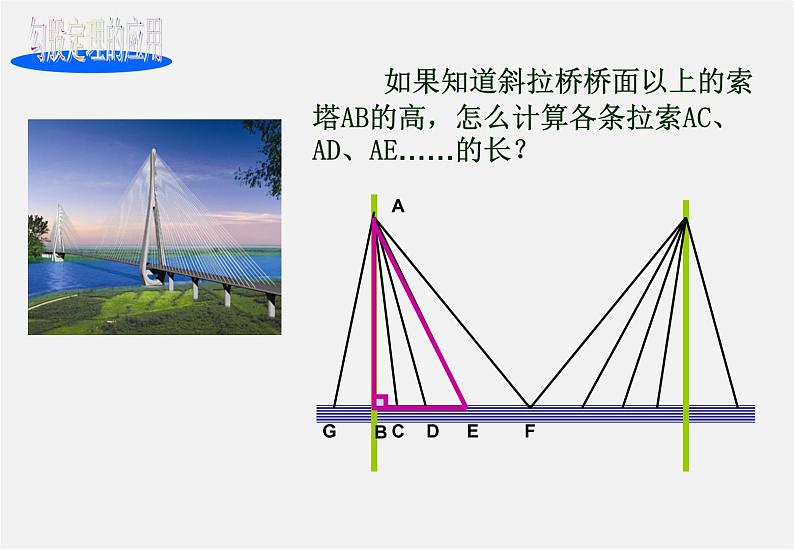
如果知道斜拉桥桥面以上的索塔AB的高，怎么计算各条拉索AC、AD、AE……的长？
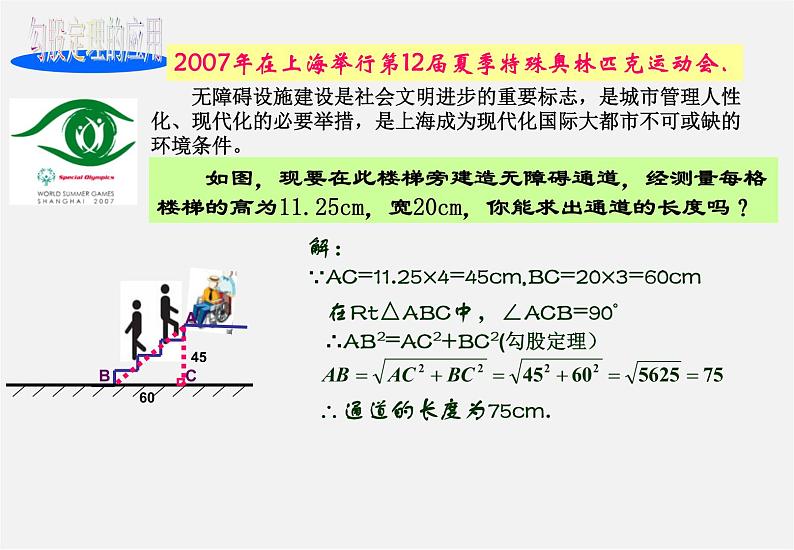
　　无障碍设施建设是社会文明进步的重要标志，是城市管理人性化、现代化的必要举措，是上海成为现代化国际大都市不可或缺的环境条件。
2007年在上海举行第12届夏季特殊奥林匹克运动会．
　　如图，现要在此楼梯旁建造无障碍通道，经测量每格楼梯的高为11.25cm，宽20cm，你能求出通道的长度吗？
在Rt△ABC中，∠ACB=90° ∴AB2=AC2+BC2(勾股定理）
解：∵AC=11.25×4=45cm,BC=20×3=60cm
∴通道的长度为75cm.
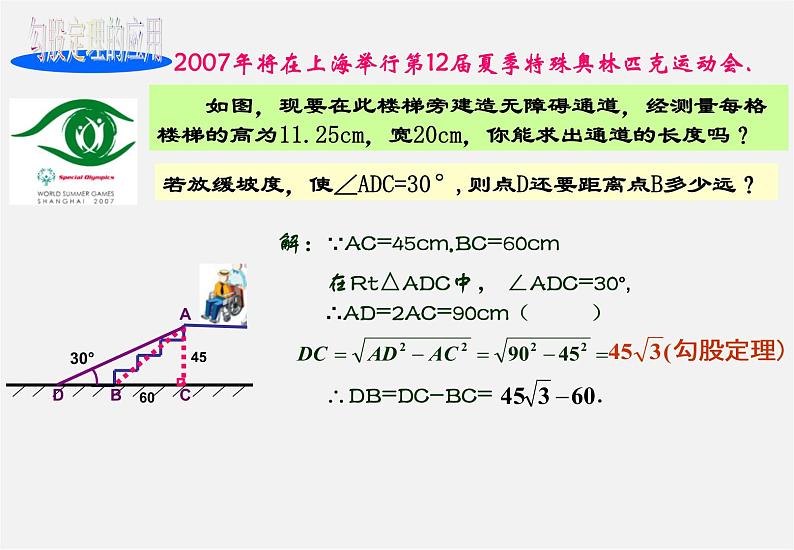
在Rt△ADC中， ∠ADC=30°, ∴AD=2AC=90cm（　　　）
解：∵AC=45cm,BC=60cm
若放缓坡度，使∠ADC=30°,则点D还要距离点B多少远？
2007年将在上海举行第12届夏季特殊奥林匹克运动会．
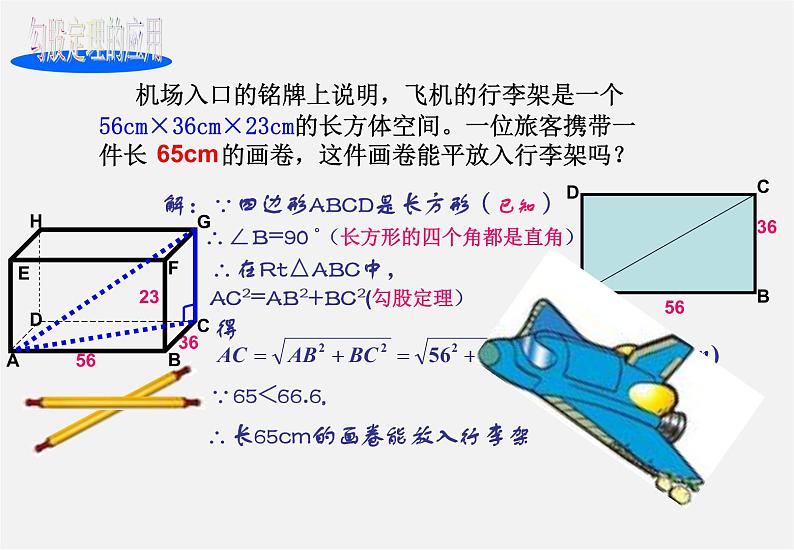
机场入口的铭牌上说明，飞机的行李架是一个56cm×36cm×23cm的长方体空间。一位旅客携带一件长 的画卷，这件画卷能平放入行李架吗？
解：∵四边形ABCD是长方形（已知）
∴∠B=90 °（长方形的四个角都是直角）
∴在Rt△ABC中， AC2=AB2+BC2(勾股定理）
∴长65cm的画卷能放入行李架
《九章算术》专设勾股章来研究勾股问题，共24个问题．按性质可分为三组，其中第一组的14个问题可以直接利用勾股定理来解决．很多是具有历史地位的世界著名算题．
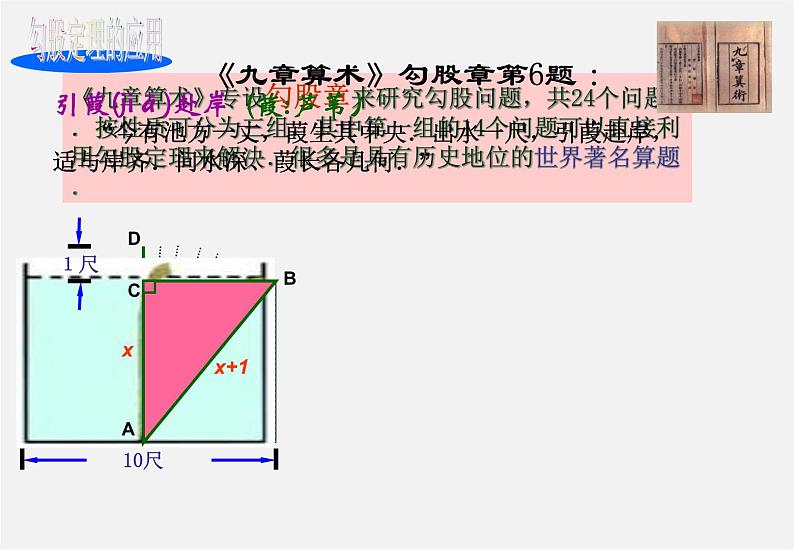
《九章算术》勾股章第6题 :
　　“今有池方一丈，葭生其中央．出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何．”
　　这一问题在世界数学史上很有影响．印度古代数学家婆什迦罗（Bhāskara，1114～1185）的《丽罗瓦提》一书中有按这一问题改编的＂风动红莲＂；
　　　　　　风动红莲平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边；渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅？
　　阿拉伯数学家阿尔•卡西的《算术之钥》也有类似的＂池中长茅＂问题；欧洲《十六世纪的算术》一书中又有＂圆池芦苇＂问题．
　　　《周髀算经》中还有＂陈子测日＂的记载
　　＂若求邪至日者，以日下为勾，日高为股，勾股自乘，并开方而除之，得邪至日者．＂
　　根据勾股定理，周子可以测量太阳的高度、太阳的直径和天地的长阔等．
　　“禹治洪水决流江河，望山川之形，定高下之势，除滔天之灾，使注东海，无漫溺之患，此勾股之所系生也．＂
　　大禹为了治理洪水，使不决流江河，根据地势高低，决定水流走向，因势利导，使洪水注入海中，不再有大水漫溺的灾害，是应用勾股定理的结果．
勾股定理在我国古代数学中占有十分重要的地位，千百年来逐渐形成了一门以勾股定理及其应用为核心的中国式的几何学．
战国时期另一部古籍《路史后记十二注》中就有这样的记载：
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,
你能想个办法吗?请你与同伴交流设计方案?
　　小明发现旗杆上的绳子垂到地面还多1米，当他们把绳子的下端拉开5米后，发现下端刚好接触地面，你能帮他们把旗杆的高度和绳子的长度计算出来吗？
通过这节课的学习你有什么收获？
　　校园里有一块三角形空地，现准备在这块空地上种植草皮以美化环境，已经测量出它的三边长分别是13、14、15米，若这种草皮每平方米售价120元，则购买这种草皮至少需要支出多少？
你能找出表示 这些数的点吗？
练习册P56 17.9（2）
　　今年开始，旧小区平改坡综合改造，将作为本市加快构筑住房保障体系、改善市民居住条件和环境的“重头戏”。
　　若屋顶的原来的长约为12米，宽为８米，新造的屋檐与原屋顶的夹角为30°，则屋檐AB的长为多少米？
　　工人铺设屋面时，若每平方米造价180元，则铺设一个屋顶需多少钱？