八年级下册18.2 勾股定理的逆定理评课课件ppt

这是一份八年级下册18.2 勾股定理的逆定理评课课件ppt，共23页。PPT课件主要包含了活动1复习巩固，探索新知，活动2动手想一想，勾股定理，互逆命题，想一想，勾股定理的逆命题，活动3验证，定理与逆定理，勾股定理的逆定理等内容，欢迎下载使用。

1.直角三角形有哪些性质?
2.如何判断三角形是直角三角形?
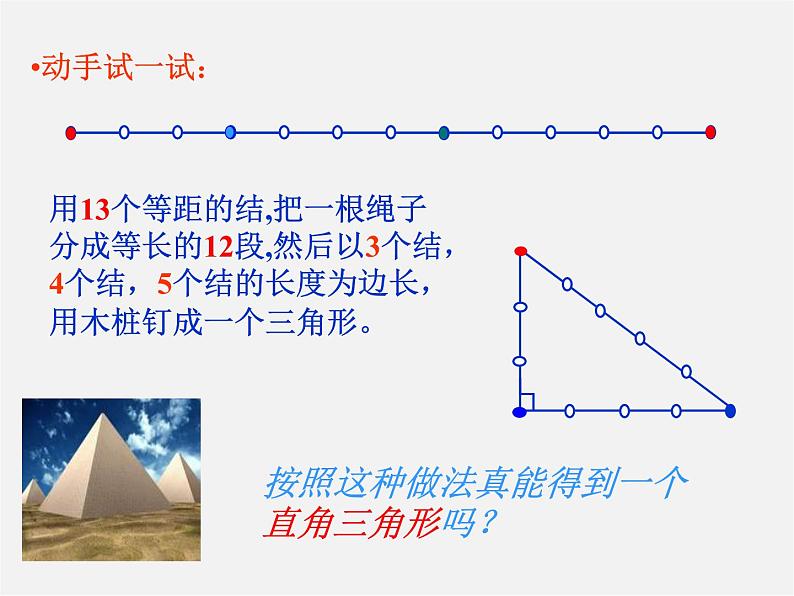
按照这种做法真能得到一个直角三角形吗？
用13个等距的结,把一根绳子分成等长的12段,然后以3个结，4个结，5个结的长度为边长，用木桩钉成一个三角形。
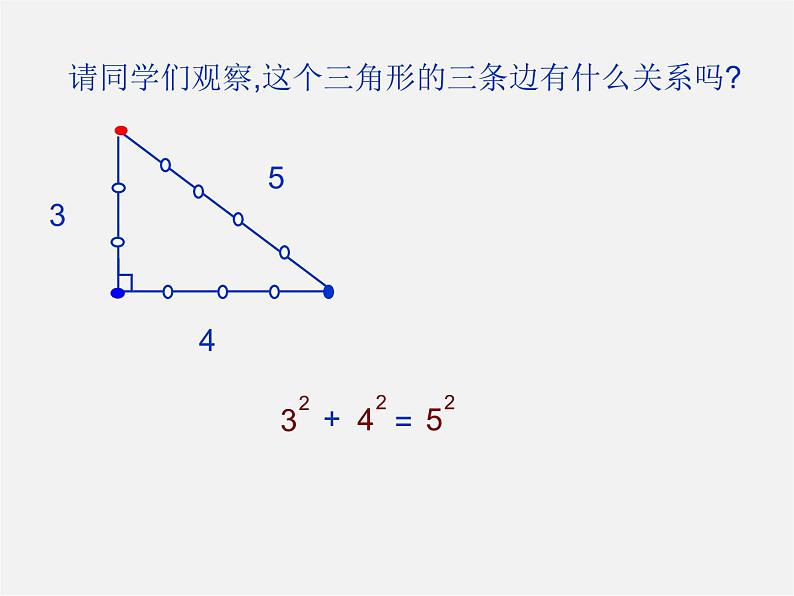
请同学们观察,这个三角形的三条边有什么关系吗?
下面的三组数分别是一个三角形的三边长a，b，c：
2.5，6，6.5； 6，8，10。
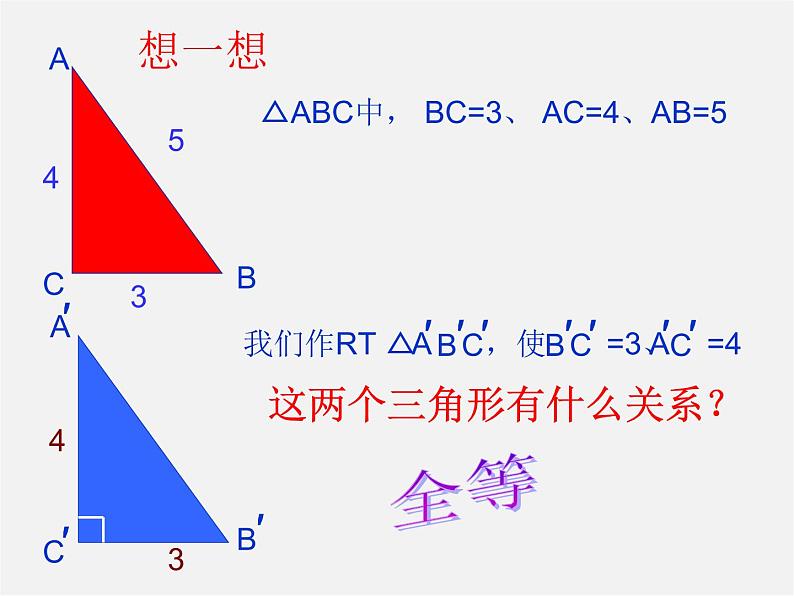
△ABC中， BC=3、 AC=4、AB=5
这两个三角形有什么关系？
我们作RT △ ，使 =3、 =4
∴ A’B’2= a2+b2
∴ A’B’ 2=c2
∴ △ ABC ≌△ A’B’C’（SSS）
∴ ∠ C= ∠ C’=90°
已知:在△ABC中，AB=c BC=a CA=b 且a2+b2=c2
求证:△ ABC是直角三角形
证明:画一个△A’B’C’,使∠ C’=90°,B’C’=a, C’A’=b
在△ ABC和△ A’B’C’中
则 △ ABC是直角三角形（直角三角形的定义）
我们已经学习了一些互逆的定理,如:勾股定理及其逆定理；两直线平行,内错角相等;内错角相等,两直线平行.
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
如果三角形的三边长a，b，c满足 a2+b2=c2那么这个三角形是直角三角形.
我们发现这个定理可以用来判定一个三角形是直角三角形.
例1 判断由a、b、c组成的三角形是不是直角三角形：(1) a＝7 , b ＝24 , c＝25
(2) a＝7, b ＝8 , c＝11
分析：由勾股定理的逆定理，判断三角形是不是直角三角形，只要看两条较小边的平方和是否等于最大边的平方。
解：∵72＋242＝49+576 252＝625 ∴ 72＋242＝252 ∴这个三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数，称为勾股数.
分析：先来判断a,b,c三边哪条最长，可以代n为满足条件的特殊值来试，n=4.则a=15,b=8,c=17,c最大。
∴△ABC是直角三角形
已知：如图，四边形ABCD中，∠B＝900，AB＝3，BC＝4，CD＝12，AD＝13,求四边形ABCD的面积?
S四边形ABCD=36
作业： 习题19.2第1题、第4题
2、什么叫做互逆命题、原命题与逆命题？
3、勾股定理的逆定理有什么用？
回顾：勾股定理的逆命题
如果三角形的较长边的平方等于其它两条较短边的平方和，那么这个三角形是直角三角形。
已知：在△ABC中，AB=c BC=a CA=b 且a2+b2=c2
求证： △ ABC是直角三角形
证明：画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形