沪科版八年级下册19.2 平行四边形课前预习ppt课件

这是一份沪科版八年级下册19.2 平行四边形课前预习ppt课件，共13页。PPT课件主要包含了说一说，动动脑，连结AC，∴∠3∠4，∴AB∥CD，同理AD∥BC，巩固练习，课后作业等内容，欢迎下载使用。
1、平行四边形的定义。
2、平行四边形有哪些性质？
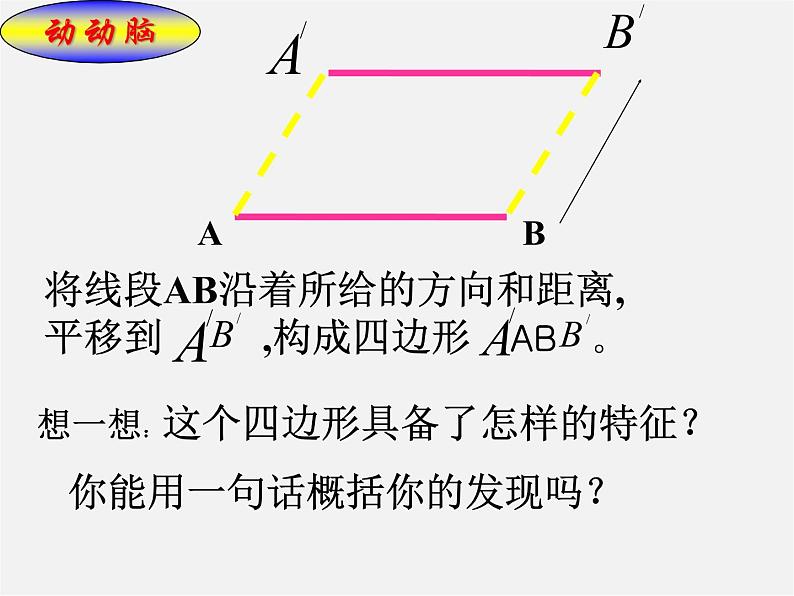
将线段AB沿着所给的方向和距离,平移到 ,构成四边形 AB 。
想一想：这个四边形具备了怎样的特征？
你能用一句话概括你的发现吗？
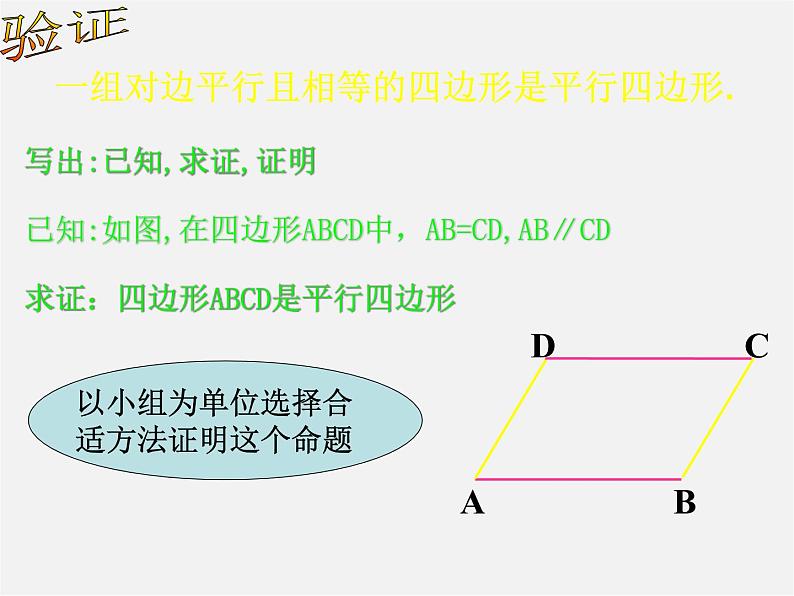
一组对边平行且相等的四边形是平行四边形.
写出:已知,求证,证明
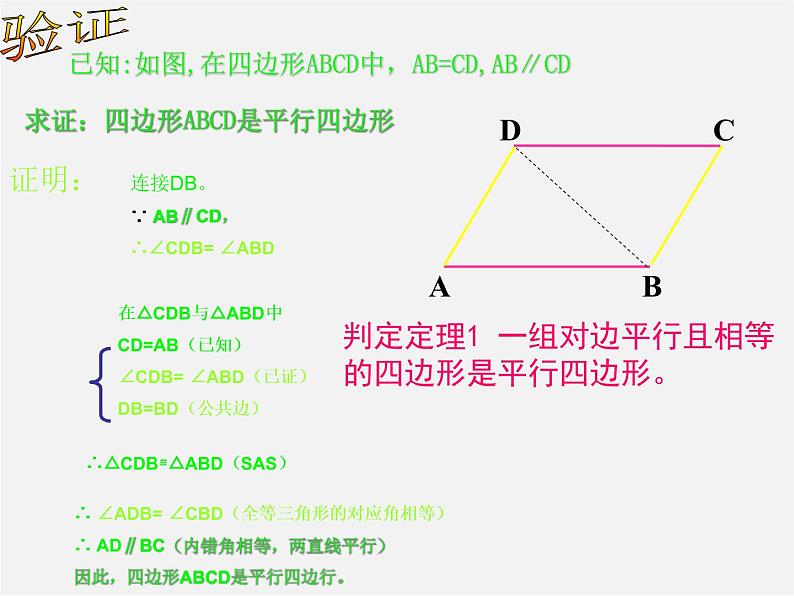
已知:如图,在四边形ABCD中，AB=CD,AB∥CD
求证：四边形ABCD是平行四边形
连接DB。∵ AB∥CD，∴∠CDB= ∠ABD
在△CDB与△ABD中CD=AB（已知）∠CDB= ∠ABD（已证）DB=BD（公共边）
∴△CDB≌△ABD（SAS）
∴ ∠ADB= ∠CBD（全等三角形的对应角相等）∴ AD∥BC（内错角相等，两直线平行）因此，四边形ABCD是平行四边行。
判定定理1 一组对边平行且相等的四边形是平行四边形。
平行四边形的对边相等。
逆命题两组对边分别相等的四边形是平行四边形。
已知：四边形ABCD, AB=CD，AD=BC求证：四边形ABCD是平行四边形
∵ 在△ABC与△CDA中AB=CD（已知）AD=BC （已知）AC=CA （公共边）∴△ABC≌△CDA（SSS）
∴∠1=∠2，∠3=∠4（全等三角形的对应边相等）∴ AB∥CD，AD∥BC （内错角相等，两直线平行）∴四边形ABCD是平行四边形
定理2 两组对边分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形
已知：如图，四边形ABCD, AC、BD交于点O且OA=OC，OB=OD求证：四边形ABCD是平行四边形
证明：∵在△AOB与△COD中 AO = CO （已知） ∠1 = ∠2 （已知） BO = DO （已知）
∴△AOB≌△COD（SAS）
∴四边形ABCD是平行四边形
定理3 对角线互相平分的四边形是平行四边形
你还能用其他的方法来证明吗?
例题：已知如图，点E、F是平行四边形对角线AB上的两点，且AE=CF。求证：四边形DEBF是平行四边形。
证明：连接BD交AC于点O
∵ 四边形ABCD是平行四边形，∴AO=CO，BO=DO。又∵AE=CF，∴OE=OF。∴四边形DEBF是平行四边形。
1．如图，在四边形ABCD中，AC、BD相交于点O， （1）若AD=8cm，AB=4cm，那么当BC=___  _cm，CD=___  _cm时，四边形ABCD为平行四边形； （2）若AC=10cm，BD=8cm，那么当AO=__  _cm，DO=__  _cm时，四边形ABCD为平行四边形． 
2、如图，在平行四边形ABCD的一组对边AD、BC上截取EF＝MN，连接EM、FN，EM和FN有怎样的关系？为什么？
谈谈你在这节课中，有什么收获？
课外作业第80面练习20.2 第1、2、4题
课堂作业1、求证：两组对角分别相等的四边形是平行四边形。2、第81面习题20.2第10、11题。