初中数学沪科版九年级上册第21章 二次函数与反比例函数21.2 二次函数的图象和性质教学演示ppt课件

这是一份初中数学沪科版九年级上册第21章 二次函数与反比例函数21.2 二次函数的图象和性质教学演示ppt课件，共22页。PPT课件主要包含了抛物线yax2，向上平移c个单位，向下平移c个单位，真知从实践走来，–10，y4x2，试一试，如何平移，比一比等内容，欢迎下载使用。

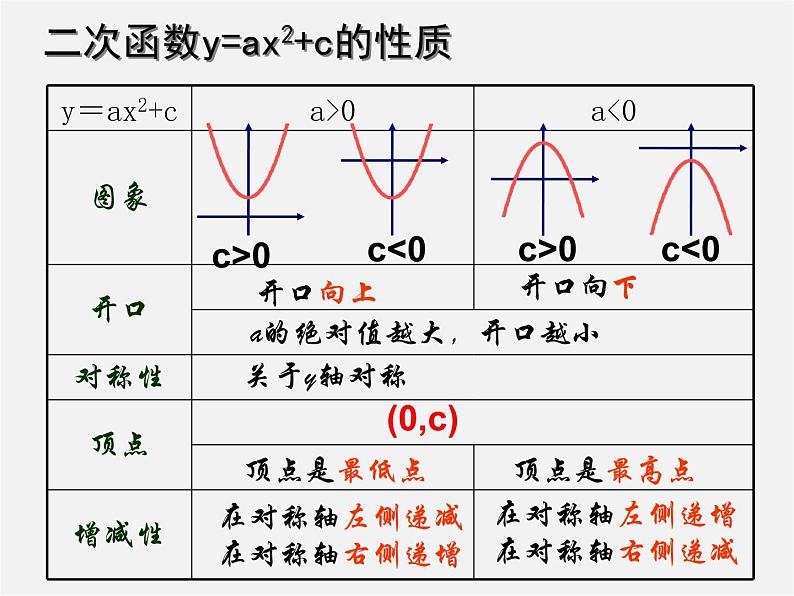
二次函数y=ax2+c的性质
a的绝对值越大，开口越小
在对称轴左侧递减在对称轴右侧递增
在对称轴左侧递增在对称轴右侧递减
抛物线y=ax2与y=ax2±c之间的关系是：
形状大小相同，开口方向相同，对称轴相同，而顶点位置和抛物线的位置不同．
抛物线之间的平移规律：(c>0)
抛物线 y=ax2－c
抛物线 y=ax2+c
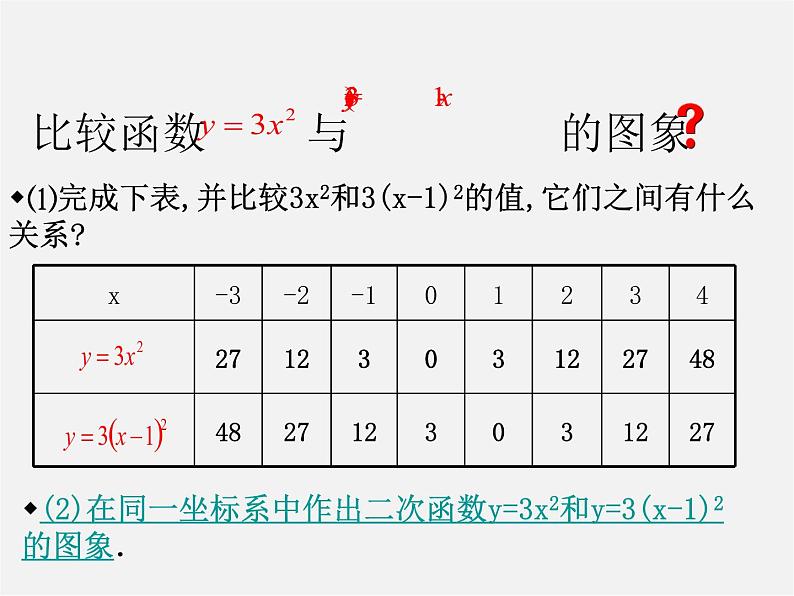
比较函数 与 的图象
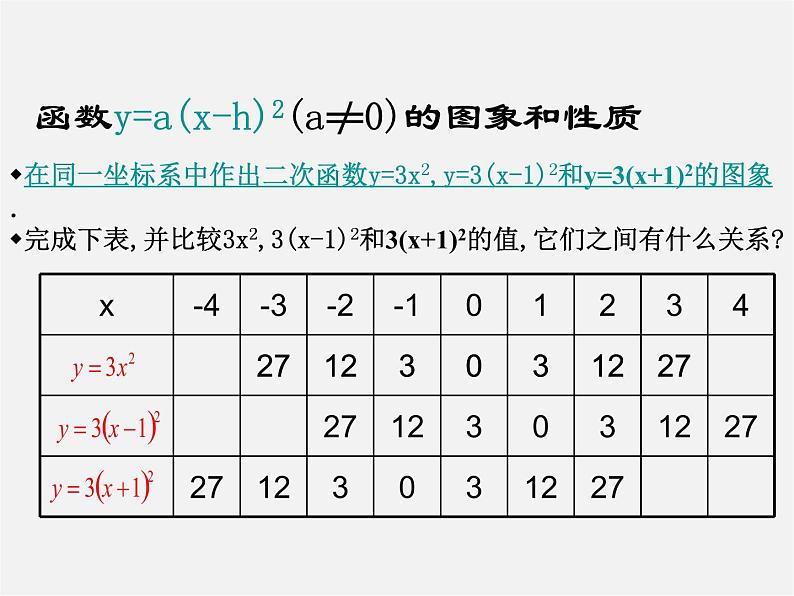
(2)在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象．
⑴完成下表,并比较3x2和3(x-1)2的值,它们之间有什么关系?
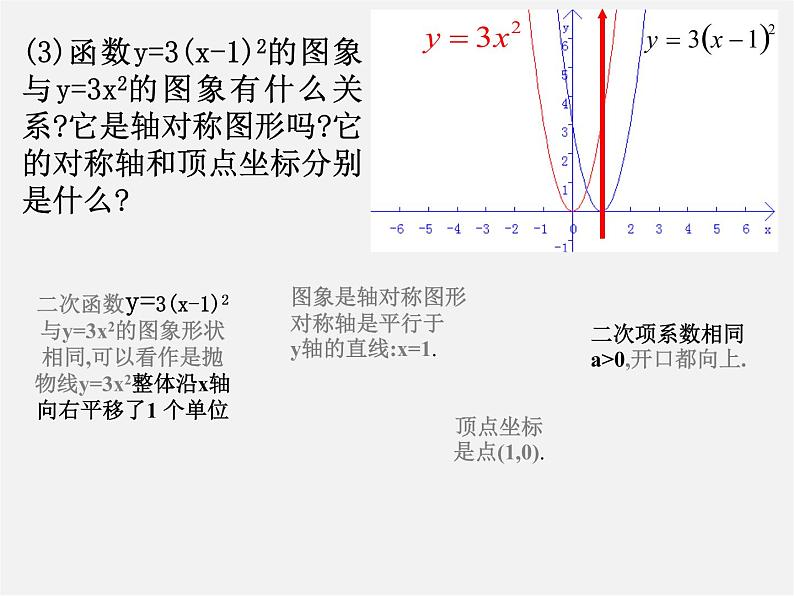
图象是轴对称图形对称轴是平行于y轴的直线:x=1.
顶点坐标是点(1,0).
二次函数y=3(x-1)2与y=3x2的图象形状相同,可以看作是抛物线y=3x2整体沿x轴向右平移了1 个单位
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
二次项系数相同a>0,开口都向上.
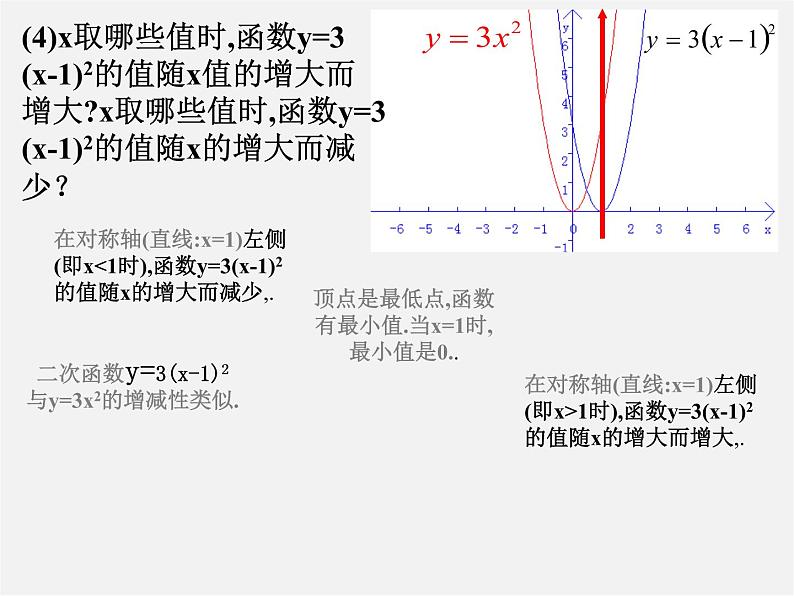
在对称轴(直线:x=1)左侧(即x<1时),函数y=3(x-1)2的值随x的增大而减少,.
顶点是最低点,函数有最小值.当x=1时,最小值是0..
二次函数y=3(x-1)2与y=3x2的增减性类似.
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少？
在对称轴(直线:x=1)左侧(即x>1时),函数y=3(x-1)2的值随x的增大而增大,.
1.在上面的坐标系中作出二次函数y=3(x+1)2的图象.它与二次函数y=3x2和y=3(x-1)2的图象有什么关系？它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x+1)2的值随x的增大而减少？
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x+1)2的图象．
完成下表,并比较3x2,3(x-1)2和3(x+1)2的值,它们之间有什么关系?
函数y=a(x-h)2(a≠0)的图象和性质
图象是轴对称图形.对称轴是平行于y轴的直线:x= -1.
顶点坐标是点(-1,0).
二次函数y=3(x+1)2与y=3x2的图象形状相同,可以看作是抛物线y=3x2整体沿x轴向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
在对称轴(直线:x=-1)左侧(即x<-1时),函数y=3(x+1)2的值随x的增大而减少,.
顶点是最低点,函数有最小值.当x=-1时,最小值是0..
二次函数y=3(x+1)2与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x+1)2的值随x的增大而减少？
在对称轴(直线:x=-1)右侧(即x>-1时),函数y=3(x+1)2的值随x的增大而增大,.
对称轴:y轴即直线: x=0
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
2.抛物线y=-3(x-1)2和y=-3(x+1)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.抛物线y=-3(x-1)2在对称轴(x=1)的左侧,当x<1时, y随着x的增大而增大;在对称轴(x=1)右侧,当x>1时, y随着x的增大而减小.当x=1时,函数y的值最大(是0);抛物线y=-3(x+1)2在对称轴(x=-1)的左侧,当x<-1时, y随着x的增大而增大;在对称轴(x=-1)右侧,当x>-1时, y随着x的增大而减小.当x=-1时,函数y的值最大(是0).
二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象
4.抛物线y=-3(x-1)2可以看作是抛物线y=-3x2沿x轴向右平移了1个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x2沿x轴向左平移了1个单位.
1.抛物线y=-3(x-1)2的顶点是(1,0);对称轴是直线:x=1;抛物线y=-3(x+1)2的顶点是(-1,0);对称轴是直线:x=-1.
1.抛物线y=a(x-h)2的顶点是(h,0),对称轴是平行于y轴的直线x=h.
3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).
二次函数y=a(x-h)2的性质
2.当a>0时,抛物线y=a(x-h)2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;当a<0时,抛物线y=a(x-h)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
课堂练习1.抛物线y= –(x+1)2的开口向 ，对称轴是 , 顶点坐标是 ；2.抛物线 向右平移2个单位,得到的抛物线是 ；
3.函数y= –5(x–3)2,当x______时,y随x的增大而增大；当x 时,y随x的增大而减小。
4 函数y=4(x+1)2的图象是由抛物线__________向___平移_____个单位得到.
5.抛物线y=-2x2向下平移2个单位得到抛物线________, 再向上平移3个单位得到抛物线____________; 若向左平移2个单位得到抛物线_____________，向右平移2个单位得到抛物线_______________.
2、按下列要求求出二次函数的解析式：（1）已知抛物线y=a(x-h)2经过点（-3，2）（-1，0）求该抛物线线的解析式。
（2）形状与y=-2(x+3)2的图象形状相同，但开口方向不同，顶点坐标是（1，0）的抛物线解析式。
（3）已知二次函数图像的顶点在x轴上，且图像经过点（2，-2）与（-1，-8）。求此函数解析式。
y= −2（x+3）2
画出下列函数图象，并说出抛物线的开口方向、对称轴、顶点，最大值或最小值各是什么及增减性如何？。
y= 2（x-3）2
y= −2（x-2）2
y= 3（x+1）2
（5）将函数y=3（x－4）2的图象沿x轴对折后得到的函数解析式是 ；将函数y=3（x－4）2的图象沿y轴对折后得到的函数解析式是 ；
（6）把抛物线y=a（x-4）2向左平移6个单位后得到抛物线y=- 3（x-h）2的图象，则 a= ，h= .若抛物线y= a（x-4）2的顶点A，且与y轴交于点B，抛物线y= - 3（x-h）2的顶点是M，则SΔMAB= .
（7）将抛物线y=2x2－3先向上平移3单位，就得到函数 的图象，在向 平移 个单位得到函数y= 2（x-3）2的图象.
（8）函数y=（3x+6）2的图象是由函数 的 图象向左平移5个单位得到的，其图象开口向 ，对称轴是 ，顶点坐标是 ，当x 时，y随x的增大而增大，当x= 时，y有最 值是 .
你认为今天这节课最需要掌握的是 ________________ ？
二次函数y=a（x-ｈ）2的性质
二次函数的性质有哪些？请填写下表：