沪科版九年级上册22.3 相似三角形的性质图文ppt课件

这是一份沪科版九年级上册22.3 相似三角形的性质图文ppt课件，共16页。PPT课件主要包含了试一试，探究新知，∴∠B∠B′，又∵∠B∠B′，相似比等内容，欢迎下载使用。

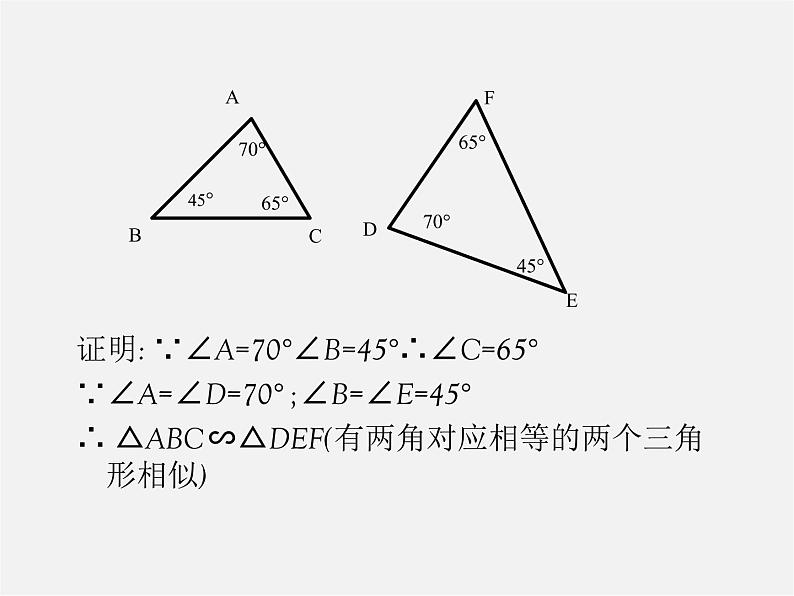
1.根据下列各图中给出的条件,确定△ABC与△DEF是否相似
证明: ∵∠A=70°∠B=45°∴∠C=65°∵∠A=∠D=70° ;∠B=∠E=45° ∴ △ABC∽△DEF(有两角对应相等的两个三角形相似)
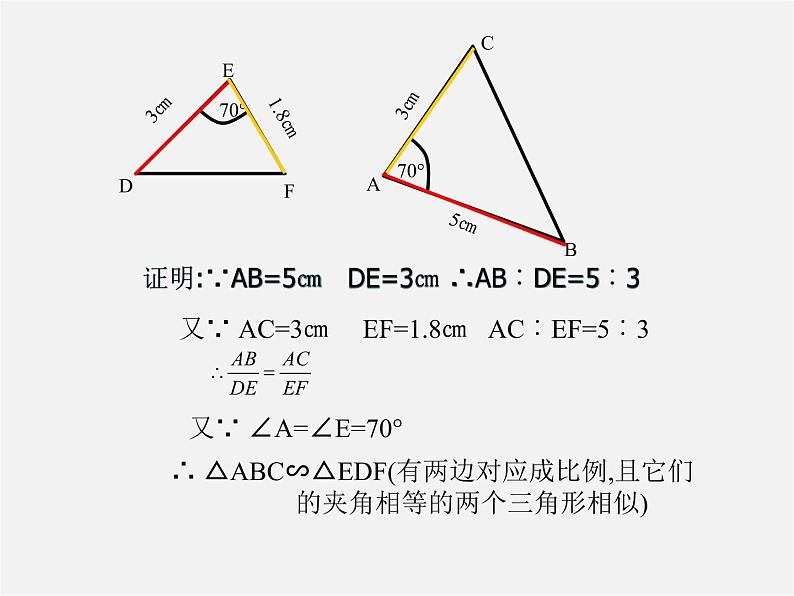
证明:∵AB=5㎝ DE=3㎝ ∴AB︰DE=5︰3
又∵ AC=3㎝ EF=1.8㎝ AC︰EF=5︰3
又∵ ∠A=∠E=70°
∴ △ABC∽△EDF(有两边对应成比例,且它们 的夹角相等的两个三角形相似)
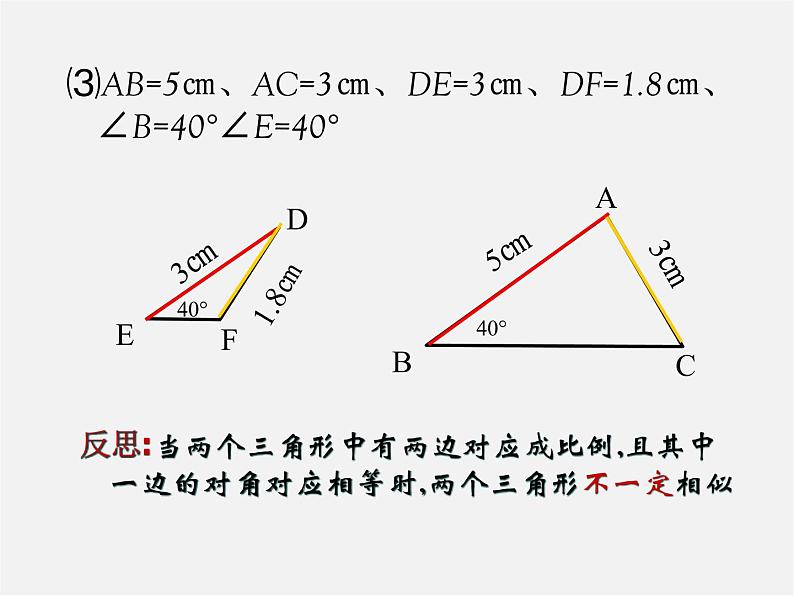
⑶AB=5㎝、AC=3㎝、DE=3㎝、DF=1.8㎝、∠B=40°∠E=40°
反思:当两个三角形中有两边对应成比例,且其中一边的对角对应相等时,两个三角形不一定相似
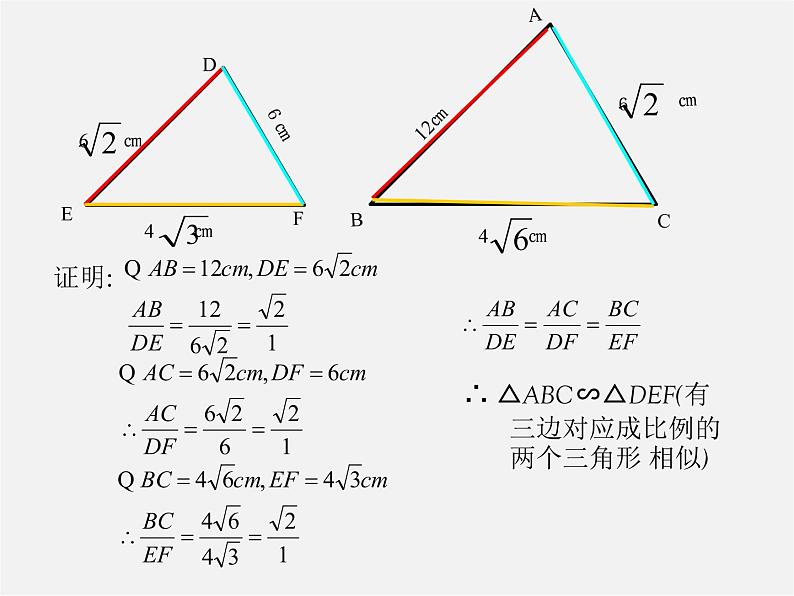
∴ △ABC∽△DEF(有三边对应成比例的两个三角形 相似)
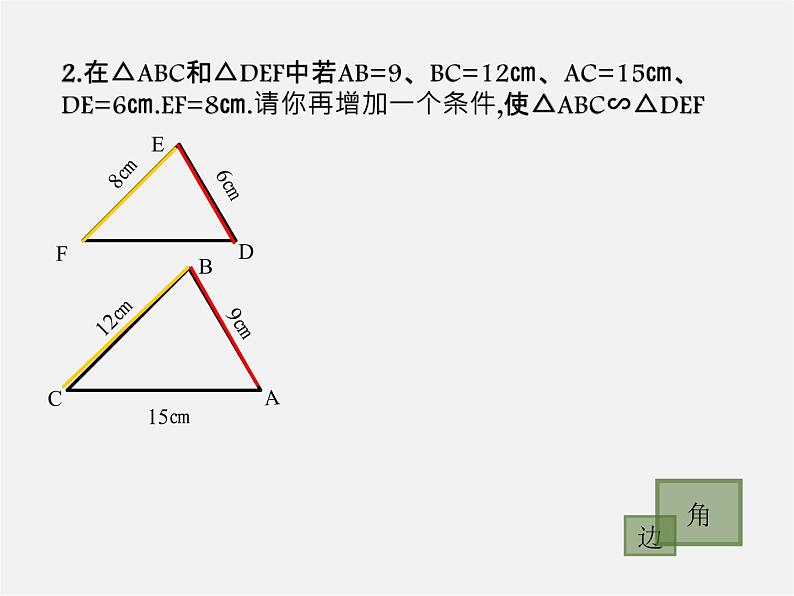
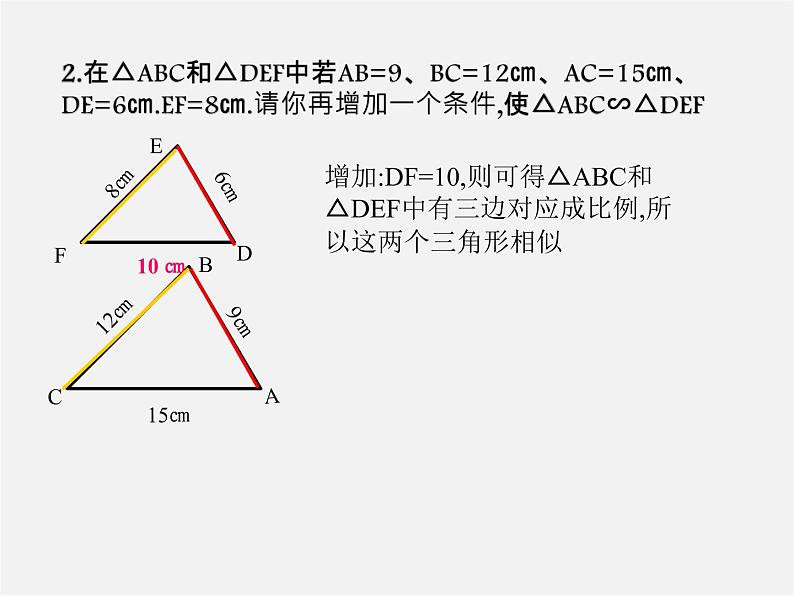
2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEF
增加:DF=10,则可得△ABC和△DEF中有三边对应成比例,所以这两个三角形相似
增加:∠B=∠E,则可得△ABC和△DEF中有两边对应成比例且它们的夹角对应相等,所以这两个三角形相似
增加: DF=10, 则可得△ABC和△DEF中有三边对应成比例,所以这两个三角形相似
增加: ∠B=∠E 则可得△ABC和△DEF中有两边对应成比例,且它们的夹角对应相等,所以这两个三角形相似
回顾与反思: 当两个三角形中已有两边对应成比例而要证明两个三角形相似时 ,可以再设法寻找第三边与它们成比例;或找这两边的夹角对应相等
3.如图,已知:在△ABC中D、E分别是AC、AB上的点,且∠ADE=∠C,AD：AC= ︰2, AB=6, DE= ,求AE,BC的长.
解:在△ABC和△ADE中∵ ∠A=∠A ∠ADE=∠C∴ △ABC∽△AED
已知如图: AD：AC=2︰3 AE= 3 AB= 4.5 求证: △ABC∽△AED.
又∵ ∠EAD =∠BAC∴△ABC∽△AED.
例题1 已知如图: △ABC∽△A′B′C′,相似比K=2︰3,又BD、B′D′分别是∠ABC、∠A′B′C′的平分线,求证BD︰B′D′=2︰3.
证明:∵△ABC∽△A′B′C′ ∴∠A =∠A′; ∠ABC=∠A′B′C′
思考:若K=a︰b,则可得AD︰A′D′的值为多少?由此可得什么结论
相似三角形的性质:相似三角形对应角平分线的比等于相似比.
∵△ABC与△A′B′C′的相似比 k=2︰3,.
∴△ABD∽△A′B′D′
∵BD、B′D′分别是∠ABC、∠A′B′C的平分线,∴∠ABD=∠A′B′D′； 又∠A =∠A′;
例题2 已知如图: △ABC∽△A′B′C′,相似比k,又AD、A′D′分别是BC、B′C′上的中线,求证AD︰A′D′=k.
证明:∵△ABC∽△A′B′C′
结论:相似三角形对应中线的比等于相似比
∵AD、A′D′分别是BC、B′C′ 的中线,
∴△ABD∽△A′B′D′
猜测:相似三角形对应高的比等于________.
∵AD⊥BC，A’D’⊥B’C’ ∴∠ADB = ∠A’D’B’又∵ ∠B = ∠B’ ∴ △ABD∽△A’B’D’
相似三角形对应高的比等于相似比.
已知如图: △ABC∽△A′B′C′,相似比k,又AD、A′D′分别是BC、B′C′上的高,求证:AD︰A′D′=k.
∵△ABC∽△A′B′C′,相似比k又AD、A′D′分别是BC、B′C′上的高