初中沪科版22.4 图形的位似变换教案设计
展开22.4位似变换
教学目标 (知识与能力;过程与方法;情感态度与价值观)
| 1.巩固位似图形及其有关概念. 2.会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律. 3.了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.
| ||
教材分析 | 重 点 | 用图形的坐标的变化来表示图形的位似变换. | |
难 点 | 把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律. | ||
教 学 方 法 |
| ||
教 具 准 备 |
| ||
学 法 指 导 |
| ||
教学过程 | |||
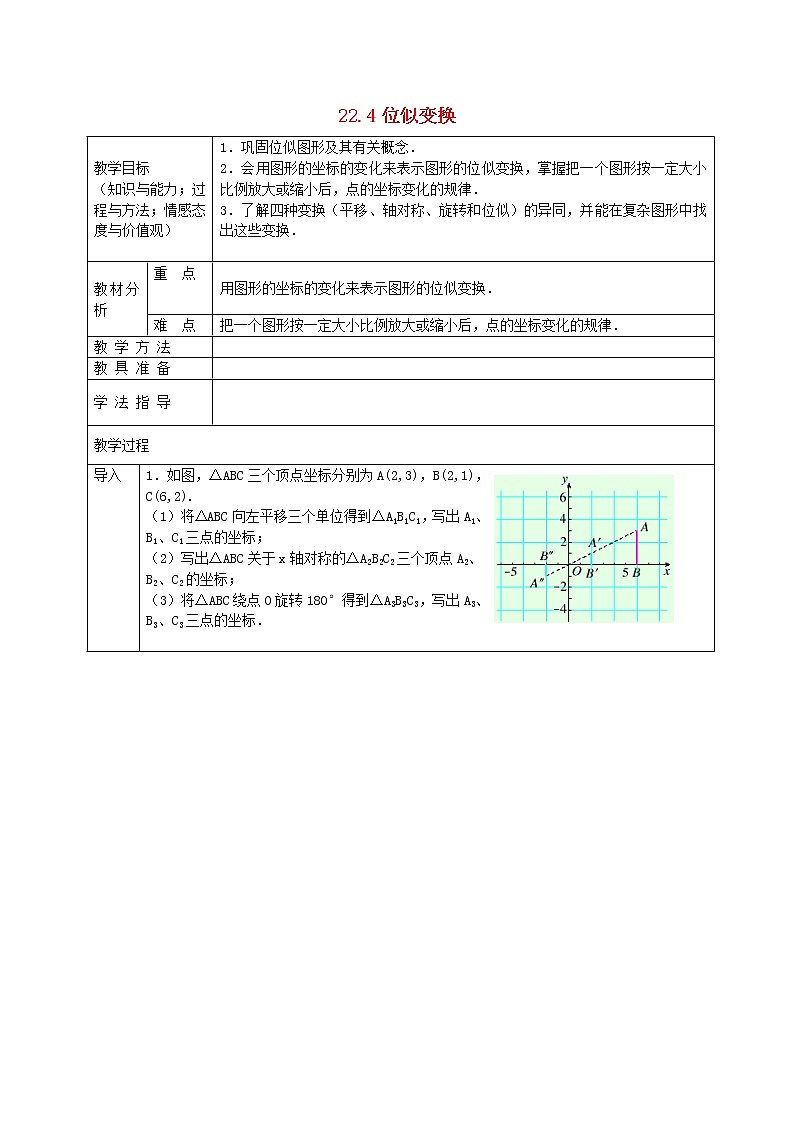
导入 | 1.如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2). (1)将△ABC向左平移三个单位得到△A1B1C1,写出A1、B1、C1三点的坐标; (2)写出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标; (3)将△ABC绕点O旋转180°得到△A3B3C3,写出A3、B3、C3三点的坐标.
| ||
新
授 | 2.在前面几册教科书中,我们学习了在平面直角坐标系中,如何用坐标表示某些平移、轴对称、旋转(中心对称)等变换,相似也是一种图形的变换,一些特殊的相似(如位似)也可以用图形坐标的变化来表示. 3.探究: (1)如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为,把线段AB缩小.观察对应点之间坐标的变化,你有什么发现? (2)如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现? 【归纳】 位似变换中对应点的坐标的变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k. 五、例题讲解 例1(教材P63的例题) 分析:略(见教材P63的例题分析) 解:略(见教材P63的例题解答) 问:你还可以得到其他图形吗?请你自己试一试! 解法二:点A的对应点A′′的坐标为(-6×,6×),即A′′(3,-3).类似地,可以确定其他顶点的坐标.(具体解法与作图略) 例2(教材P64)在右图所示的图案中,你能找出平移、轴对称、旋转和位似这些变换吗? 分析:观察的角度不同,答案就不同.如:它可以看作是一排鱼顺时针旋转45°角,连续旋转八次得到的旋转图形;它还可以看作位似中心是图形的正中心,相似比是4∶3∶2∶1的位似图形,……. 解:答案不惟一,略. 六、课堂练习 教材P64.1、2 △ABO的定点坐标分别为A(-1,4),B(3,2),O(0,0),试将△ABO放大为△EFO,使△EFO与△ABO的相似比为2.5∶1,求点E和点F的坐标. 如图,△AOB缩小后得到△COD,观察变化前后的三角形顶点,坐标发生了什么变化,并求出其相似比和面积比. 七、课后练习 1.教材P65.3, P66.5、8 2.请用平移、轴对称、旋转和位似这四种变换设计一种图案(选择的变换不限). 3.如图,将图中的△ABC以A为位似中心,放大到1.5倍,请画出图形,并指出三个顶点的坐标所发生的变化. 教学反思
| ||
板书设计 |
| ||
作业布置 |
| ||
教学反思 |
| ||
初中数学沪科版九年级上册22.4 图形的位似变换教案: 这是一份初中数学沪科版九年级上册22.4 图形的位似变换教案,共3页。教案主要包含了课堂练习等内容,欢迎下载使用。
初中数学沪科版九年级上册22.1 比例线段教学设计: 这是一份初中数学沪科版九年级上册22.1 比例线段教学设计,共3页。教案主要包含了合作探究,巩固提高,随堂训练等内容,欢迎下载使用。
数学第22章 相似形22.1 比例线段教案: 这是一份数学第22章 相似形22.1 比例线段教案,共4页。













