2021学年24.7.1 弧长与扇形面积课文配套课件ppt

这是一份2021学年24.7.1 弧长与扇形面积课文配套课件ppt，共14页。PPT课件主要包含了C2πR，SπR2等内容，欢迎下载使用。

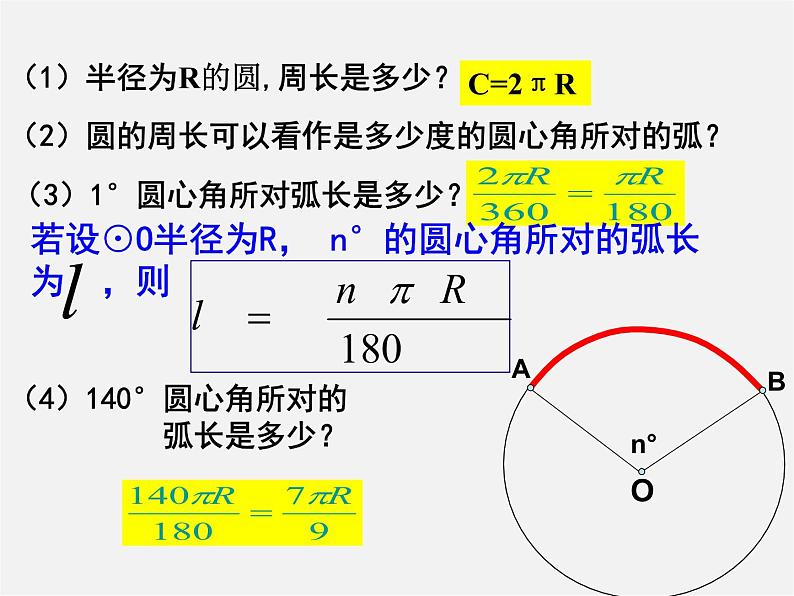
（1）半径为R的圆,周长是多少？
（3）1°圆心角所对弧长是多少？
（4）140°圆心角所对的 弧长是多少？
（2）圆的周长可以看作是多少度的圆心角所对的弧？
例1、制造弯形管道时，要先按中心线计算“展直长度”，再下料，试计算图所示管道的展直长度L(单位：mm，精确到1mm)
解：由弧长公式，可得弧AB 的长
因此所要求的展直长度
答：管道的展直长度为2970mm．
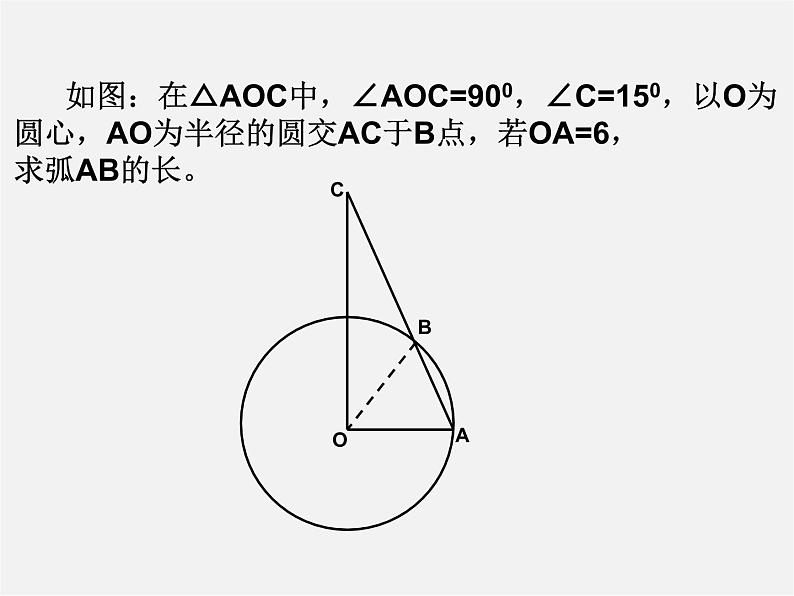
如图：在△AOC中，∠AOC=900，∠C=150，以O为圆心，AO为半径的圆交AC于B点，若OA=6，求弧AB的长。
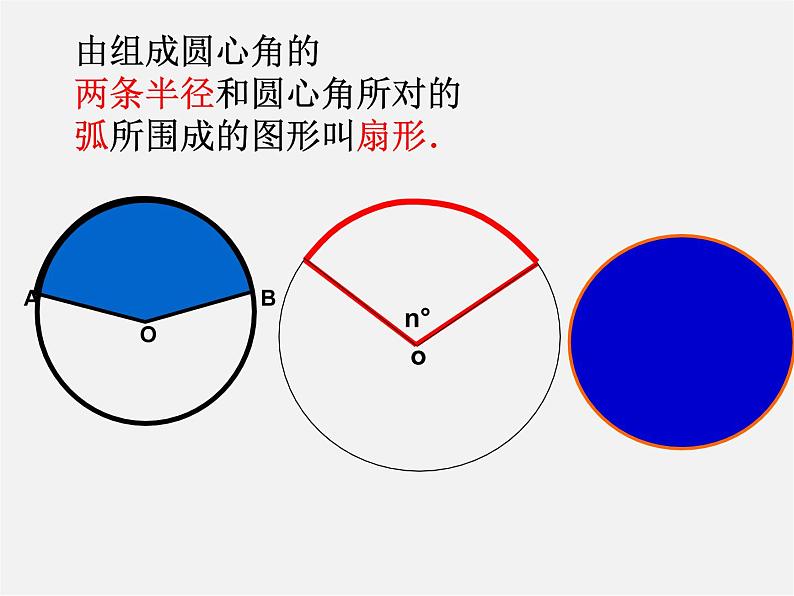
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．
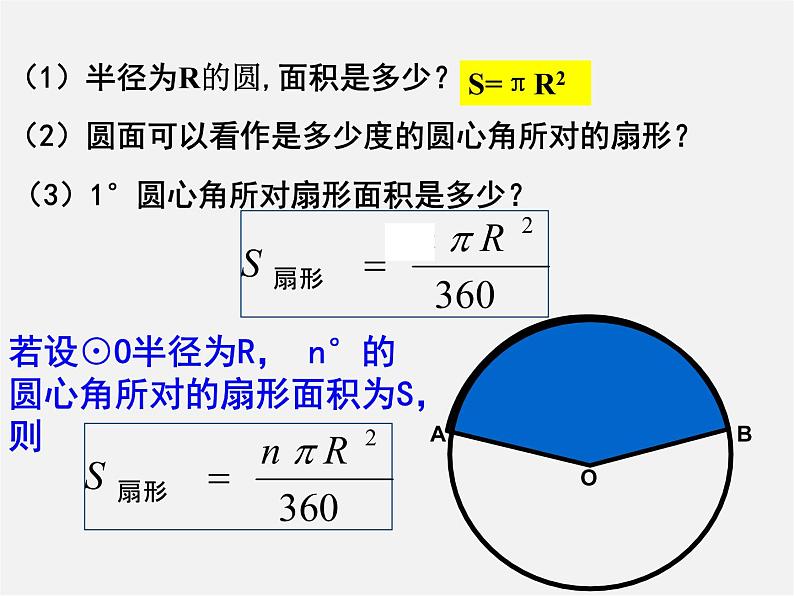
（1）半径为R的圆,面积是多少？
（3）1°圆心角所对扇形面积是多少？
（2）圆面可以看作是多少度的圆心角所对的扇形？
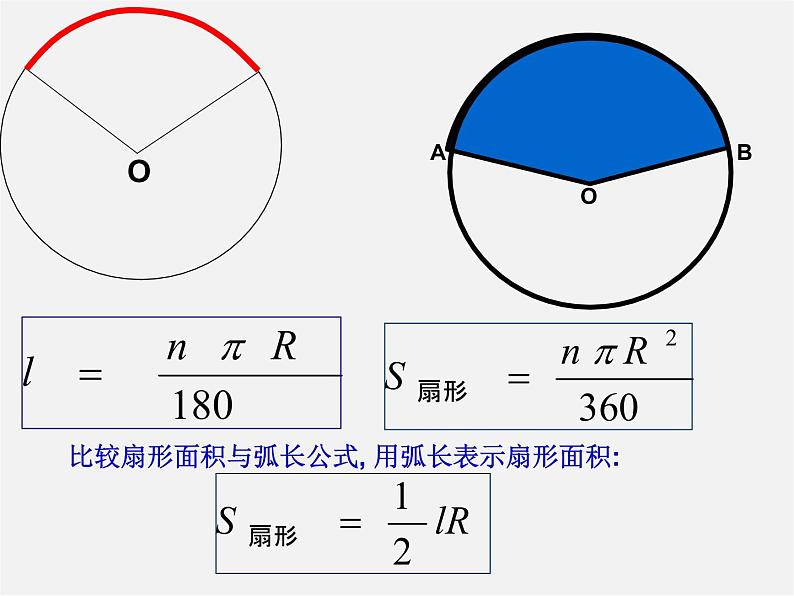
若设⊙O半径为R， n°的圆心角所对的扇形面积为S，则
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、已知扇形的圆心角为120°，半径为2，则这个扇形的面积S扇形=_ .
2、已知扇形面积为 ，圆心角为60°，则这个扇形的半径R=____．
3、已知半径为2cm的扇形，其弧长为 ，则这个扇形的面积，S扇形=——．
例2：如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.3cm，求截面上有水部分的面积。（精确到0.01cm）。
弓形的面积 = S扇- S⊿
变式：如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.9cm，求截面上有水部分的面积。（精确到0.01cm）。
弓形的面积 = S扇+ S△
2、如图，⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交，且半径都是2cm，求图中阴影部分的面积。
已知正三角形ABC的边长为a，分别以A、B、C为圆心，以a/2为半径的圆相切于点D、 E、F，求图中阴影部分的面积S.
3、如图，A是半径为1的圆O外一点，且OA=2，AB是⊙O的切线，BC//OA，连结AC，则阴影部分面积等于 。