初中数学浙教版八年级上册1.5 三角形全等的判定评课课件ppt

这是一份初中数学浙教版八年级上册1.5 三角形全等的判定评课课件ppt，共19页。PPT课件主要包含了问题导学，问题呈现，一题多解，△ADC≌△ADB，∠CAD∠BAD，DMDN，AD垂直平分BC，ABAC，盘点收获等内容，欢迎下载使用。
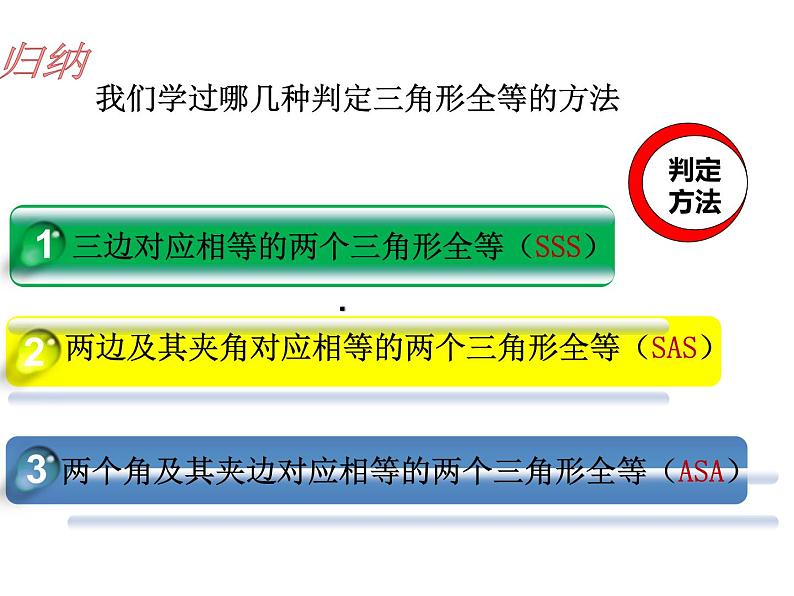
我们学过哪几种判定三角形全等的方法
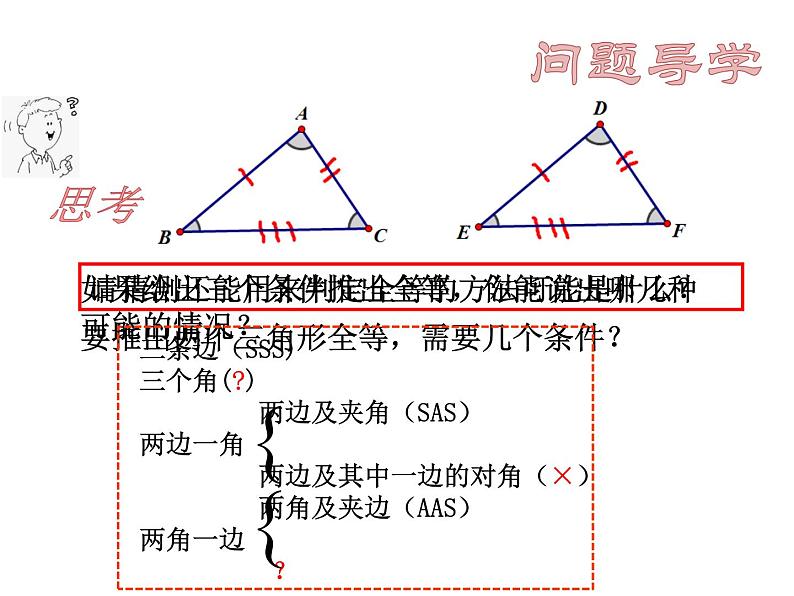
要推出两个三角形全等，需要几个条件？
如果给出三个条件推出全等，你能说出哪几种可能的情况？
三条边（SSS) 三个角(?) 两边及夹角（SAS） 两边一角 两边及其中一边的对角（×） 两角及夹边（AAS） 两角一边 ？
请猜测还能用来判定全等的方法可能是什么？
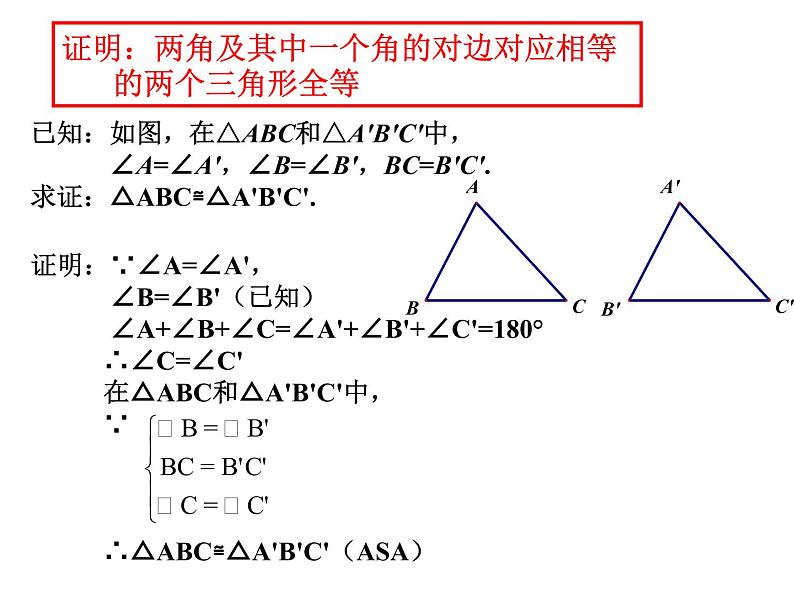
已知：如图，在△ABC和△A'B'C'中， ∠A=∠A'，∠B=∠B'，BC=B'C'.求证：△ABC≌△A'B'C'.
证明：∵∠A=∠A'， ∠B=∠B'（已知） ∠A+∠B+∠C=∠A'+∠B'+∠C'=180° ∴∠C=∠C' 在△ABC和△A'B'C'中， ∵ ∴△ABC≌△A'B'C'（ASA）
证明：两角及其中一个角的对边对应相等 的两个三角形全等
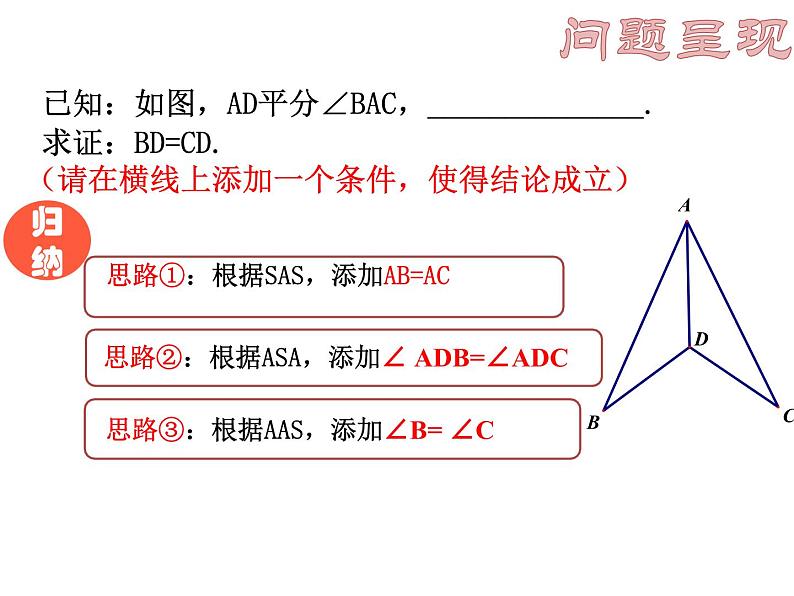
已知：如图，AD平分∠BAC，______________. 求证：BD=CD.（请在横线上添加一个条件，使得结论成立）
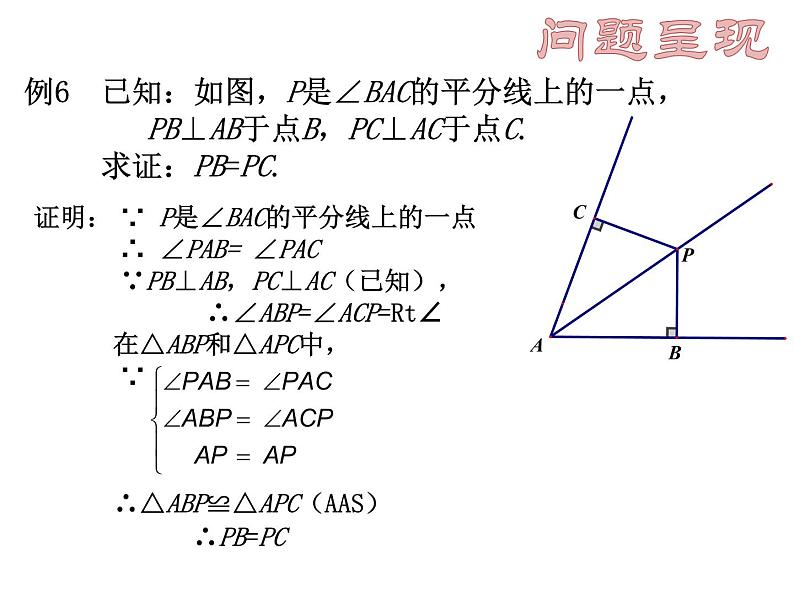
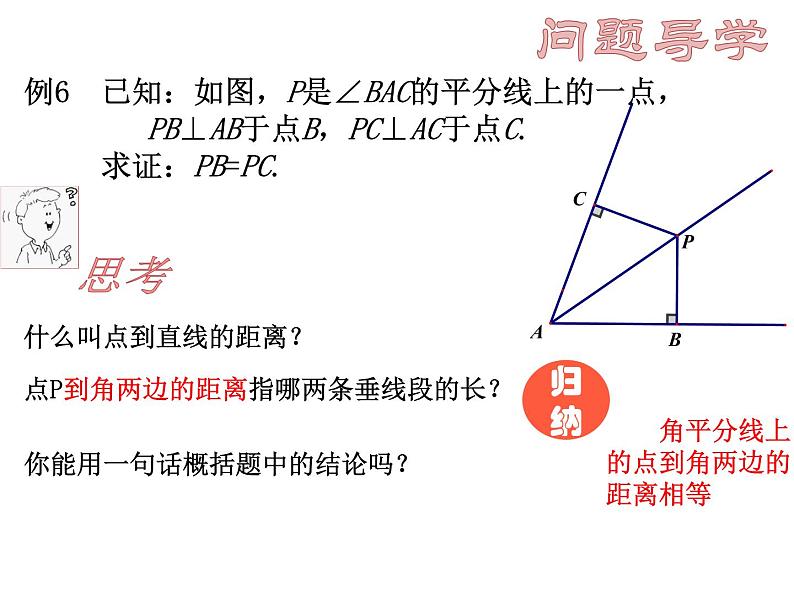
例6 已知：如图，P是∠BAC的平分线上的一点， PB⊥AB于点B，PC⊥AC于点C. 求证：PB=PC.
证明： ∵ P是∠BAC的平分线上的一点 ∴ ∠PAB= ∠PAC ∵PB⊥AB，PC⊥AC（已知）， ∴∠ABP=∠ACP=Rt∠ 在△ABP和△APC中， ∵ ∴△ABP≌△APC（AAS） ∴PB=PC
什么叫点到直线的距离？
角平分线上的点到角两边的距离相等
点P到角两边的距离指哪两条垂线段的长？
你能用一句话概括题中的结论吗？
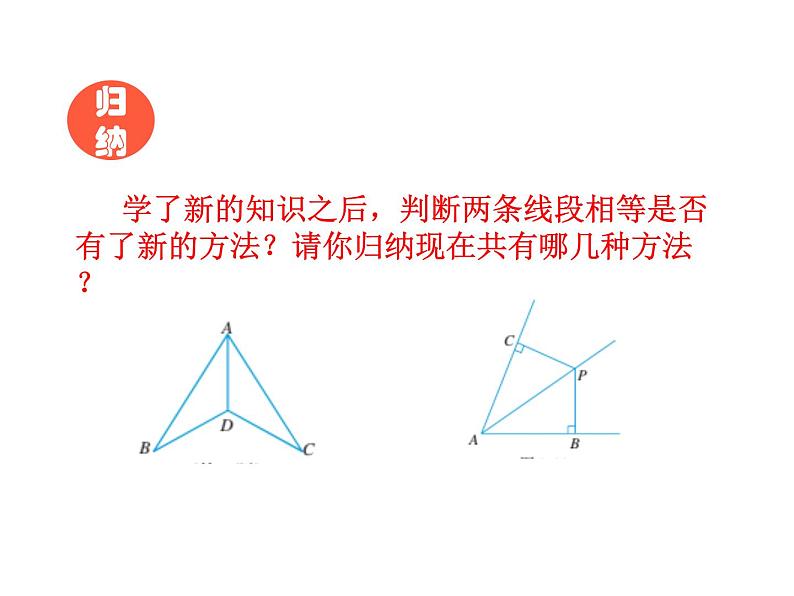
学了新的知识之后，判断两条线段相等是否有了新的方法？请你归纳现在共有哪几种方法？
例7 已知：如图，AB∥CD，PB和PC分别平分∠ABC和∠DCB，AD过点P，且与AB垂直.求证：PA=PD.
从已知条件分析：（1）由AB∥CD，可以推出什么？（2）由AD⊥AB，可以推出什么？（3）点P是∠ABC的平分线上的点，那么PA应等于什么？我们可以怎样添辅助线？（4）点P是∠DCB的平分线上的点，那么PD应等于什么？
AD过点P，且与AB垂直
∠BAD+∠CDA= 180°
几何证明的方法：综合法
为了证明PA=PD,不是直接证明这两条线段相等，而是分别证明它们与哪条线段相等？这种思考方法对你有怎样的启发？
当图形中没有现成的全等三角形时，必须通过添加适当的辅助线，构造出所需要的全等三角形
已知：如图，AD垂直平分BC，D为垂足. DM⊥AC，DN⊥AB，M，N分别为垂足.求证：DM=DN.
从已知条件分析：（1）AD垂直平分BC，你能得到哪些结论？（2）DM⊥AC，DN⊥AB，你又能得到哪些结论？
从结论出发分析：要证明DM=DN，你会想到哪些方法？
∠ADC=∠ADB=90°BD=CD
DM⊥AC，DN⊥AB
S△ADC=S△ADB
当题中出现全等三角形的时候，可以利用全等三角形对应边相等
当题中出现角平分线的时候，可以利用角平分线的性质定理
当题中具有面积相等的三角形时，可以试试面积法
证明两条线段相等的方法有哪些？
碰到几何证明题，我们可以如何进行分析呢？
从已知条件和结论两个角度入手进行分析.