2020-2021学年21.1 一次函数教学设计及反思

教学环节

教师活动

学生活动

设计意图

创

设

情

境

让我们信心饱满，伴随着儿时的童谣追忆童年。放音乐。      　　　　　　　　　　　　　　　　　　（1）你们能接着数下去吗？                     　　六只青蛙呢？          　　　　　　　　　　　　　x只青蛙呢？           　　　　　　　　　　　　x只青蛙有多少条腿？   　　　　　　　　　　　　x只青蛙共有的腿数y与x有怎样的函数关系呢？（板书；y=4x)

(2)像这样的函数关系，就是我们今天要认识的新朋友—— 一次函数。

我们该树立怎样的学习目标呢？请班长来播报。

（板书：25.1一次函数）

学生欣赏歌谣，

（1）       学生回答：能。

六只青蛙，六张嘴，

十二只眼睛，二十四条腿，六声扑通跳下水。x只青蛙共有4x条腿。

y＝ 4x.

(2)班长读学习目标。

通过歌谣《数青蛙》激发学生的求知欲，

唤起学生兴趣，引发函数关系，从而揭示课题。使学生快速进入本课的学习。

引

导

自

学

试着做一做：

众所周知：08年奥运会近在咫尺，很多人都想亲临赛场一饱眼福。你们想不想？

我们的同学小明也有这样的梦想，请这位阳光男孩来介绍一下。

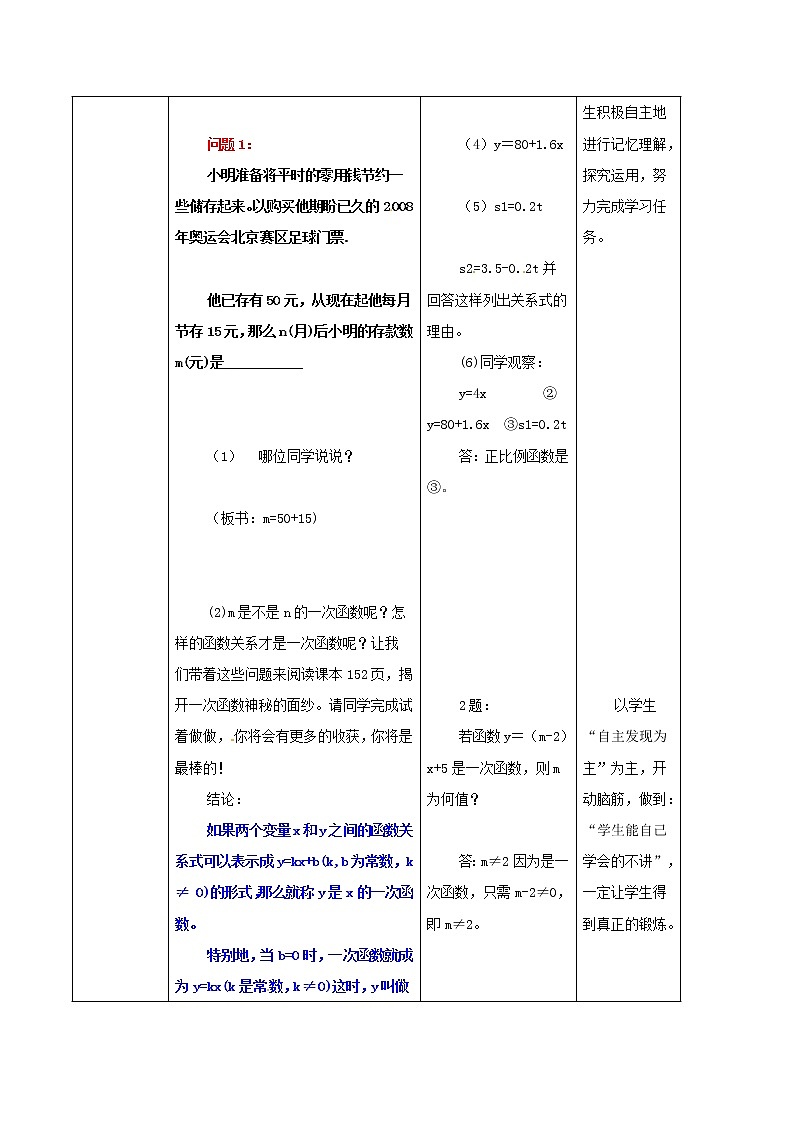
问题1：

小明准备将平时的零用钱节约一些储存起来。以购买他期盼已久的2008年奥运会北京赛区足球门票.

他已存有50元，从现在起他每月节存15元，那么n(月)后小明的存款数m(元)是___________

（1）         哪位同学说说？

（板书：m=50+15)

(2)m是不是n的一次函数呢？怎样的函数关系才是一次函数呢？让我们带着这些问题来阅读课本152页，揭开一次函数神秘的面纱。请同学完成试着做做，你将会有更多的收获，你将是最棒的！

结论：

如果两个变量x和y之间的函数关系式可以表示成y=kx+b(k,b为常数，k ≠ 0)的形式，那么就称y是x的一次函数。

特别地，当b=0时，一次函数就成为y=kx(k是常数，k ≠ 0)这时，y叫做x的正比例函数。

（4）同学们看得特认真，第1题你是如何填的？谁来试着说一下？同意的举手，咱们的同学分析问题能力很强。

（5）第2题中s1与t之间的函数关系怎样列？回答得完全正确，那s2与t呢？为什么这样列？答得非常精彩。

（6）请同学们细心观察，找出这些函数的共同点并回答问题。

1、这些函数的表达式中自变量是谁？谁是谁的函数？

2、在这些函数表达式中，表示函数的自变量的式子是整式吗？是关于自变量的几次式？他们的共同特点是什么？

（1）         同学回答：

（2）答：m=50+15n      

(3)学生看书三至四分钟。　　　

（4）y＝80+1.6x　　　　

（5）s1=0.2t

s2=3.5-0.2t并回答这样列出关系式的理由。  

(6)同学观察：

y=4x        ②y=80+1.6x  ③s1=0.2t

答：正比例函数是③。

2题：

若函数y＝（m-2）x+5是一次函数，则m为何值？

答：m≠2因为是一次函数，只需m-2≠0，即m≠2。　　　[来源:学|科|网]

3题：

若函数y=2x+5-m是正比例函数，则m为　　　　　　　

答：m=5　　　　　

因为当5-m=0时，才是y＝kx的形式，所以m=5。　　　　　

（9）多名同学列举一次函数表达式。

以问题做向导，安排自主学习，使学生积极自主地进行记忆理解，探究运用，努力完成学习任务。

以学生“自主发现为主”为主，开动脑筋，做到：“学生能自己学会的不讲”，一定让学生得到真正的锻炼。

自

主

探

究

  一起探究：

同学们在实际生活中一次函数也有非凡的表现，我们一起俯看气势磅薄的长江三峡大坝，

问题2：

长江三峡大坝从2003年6月1日开始下闸蓄水，到6月10日，水库的水位由106米升至135米，假设这段时间按220小时计算，且水位的上升可以看做匀速的。

请各小组针对这些问题展开合作交流，并把你们交流的结果填在智慧卡上，我们再来比一比哪一小组智慧多。

1 、在这段时间内,水库水位平均每小时上升多少米?

2、在这段时间内水库的水位y（米）与下闸蓄水的时间t（小时）之间的函数关系式是怎样的？

3、请指出这个一次函数的自变量的取值范围

（1）请一名播音员为我们播报长江三峡大坝。

（2）请各小组针对这些问题展开合作交流，并把你们交流的结果填在智慧卡上，我们再来比一比哪一小组智慧多。

（3）在展台上展示第一个做完的小组的答案，夺冠组可以由多名发言人进行答辩，同学不要啬吝你们的掌声啊！

（3）展示各个小组镶嵌的图案，大家列的函数关系式都是s=4n，同学们你们真了不起，当n＝10时，s是多少？

‘

可以提出这样的质疑：A、29怎么来的？　　B、为什么这样列表达式？　　　　　　　　　

C、自变量的取值范围为什么不超过200？……　　（4）能　　　　　　　　　

各组同学合作镶嵌图案（约三分钟）s=4n　　　　当n＝10时，s＝40

以问题做向导，安排自主学习，使学生积极自主地进行记忆理解，探究运用，努力完成学习任务。

让学生在已有的知识水平的基础上发现问题，分析问题，掌握知识提升能力。

通过考察对一次函数及正比例函数概念的理解，使同学们利用数学的抽象性。

让同学们举例说出一个一次函数的表达式，目的在于举一反三，使同学达到对新概念的理解

合

作

交

流

大家谈一谈：

问题3

如图：用边长相等的黄色正三角形与绿色正六边形镶嵌图案，按第1、2个图案所示规律依次下去，你能镶嵌出第3个图案吗？则第n个图案中黄色正三角形的个数m与n的函数关系式

　　　　　　　　　　　　　　展示各个小组镶嵌的图案，大家列的函数关系式都是s=4n，同学们你们真了不起，当n＝10时，s是多少？

咱们班的同学不用发愁下岗，你们至少可以当一名出色的设计师。

（1）一学生读题　　　　（2）学生交流讨论，填写智慧卡约3-4分钟

（3）可以提出这样的质疑：A、29怎么来的？　　B、为什么这样列表达式？　　　　　　　　　C、自变量的取值范围为什么不超过200？……　　（4）能　　　　　　　　　各组同学合作镶嵌图案（约三分钟）s=4n　　　　当n＝10时，s＝40

通过组内互动和组间交流，达到学生自主探索，解决疑问的目的。

通过师生互动，动手操作探寻规律，满足学生感受一次函数现实主义的愿望。

拔

高

创

新

例题讲解：

例 如图25－1，⊿ABC是边长为x的等边三角形。

（1）求BC边上的高h与x之间的函数关系式。h是x的一次函数吗？

（2）求△ABC的面积S与x之间的函数关系式，S是x的一次函数吗？

（3）如果边长是2x，高AD等于多少呢？（板书：h=√3x,h是x的一次函数）,h与x之间的函数关系式如何？h是x的一次函数吗？怎样求三角形ABC的面积S与x之间的函数关系式呢？s是x的一次函数吗？

（板书S＝，即　s不是x的一次函数）

（1）学生读题

请这位同学来读题。

（2）等边三角形是特殊的什么三角形？AD是等边三角形BC边上的高，你能根据等腰三角形的哪一特性求BD呢？

　（3）在直角三角形ABD中，根据勾股定理得

AD2＝AB2-BD2＝22-12＝3

所以AD＝√3　　　　　　　（4）AD＝√3x

h＝√3x,h是x的一次函数。S＝1/2*BC*AD

＝√3x2

s不是x的一次函数，因为x的次数不是一次。

比如：长江三峡大坝蓄水是方法①，铺正三角形和正方形镶嵌是用方法②，等边三角形钢筋结构则用的是方法③

总结：

猜想大概是下面的方法：找等量　　　直接列

观察实际　寻规律

看图形　抓特点

定理定义　　来帮忙

一次函数　　分辨清

一次整式　　不能忘

通过将实际问题转化为教学问题渗透数学建模思想，进而一层一层的拔高，使学生对一次函数有了更深的理解，使同学们体会到数学的抽象性和广泛应用性。

沙

场

练

兵

俗话说方法是最好的老师，有了好方法，就如同士兵有了精锐的武器，在战场上才会战无不胜，让我们真枪实弹，走进沙场，进行数学练兵，你们有没有信心？

（1）我们看这一枚枚光闪闪的奖牌在等着大家去摘取，去抢夺。下面，请每个小组选派一名同学来进行电脑操作。注意：你喜欢你喜欢哪枚奖牌就点击它，然后会出现一道特简单的选择题，再点击你选的答案，金牌就属于你了。我们再次在竟争中大显身手。

（2）刚才进行的必答题：最精彩的是下面的抢答题的比赛：请听：

①　　　②

多少小时能卖完？

生答：有

（1）每人一组开始逐个进行操作解答

（2）s1＝8.54t

s2＝110-8.54t

w=18n

y=900-15x即当y＝0时，900-15x＝0，x＝60，销售60小时可以卖完。

目的是查漏补缺，质量验收，让同学在应用中体验理解、提高，为教师提供反馈资料。

课

堂

小

结

同学谈收获

通过这节课的学习，请你谈谈自己有哪些收获？

布

置

作

业

请你利用一次函数的有关知识结合生活实际自己编一道应用题并进行解答。

教

学

反

思