冀教版九年级下册第29章 直线与圆的位置关系29.4 切线长定理教学演示课件ppt

这是一份冀教版九年级下册第29章 直线与圆的位置关系29.4 切线长定理教学演示课件ppt，

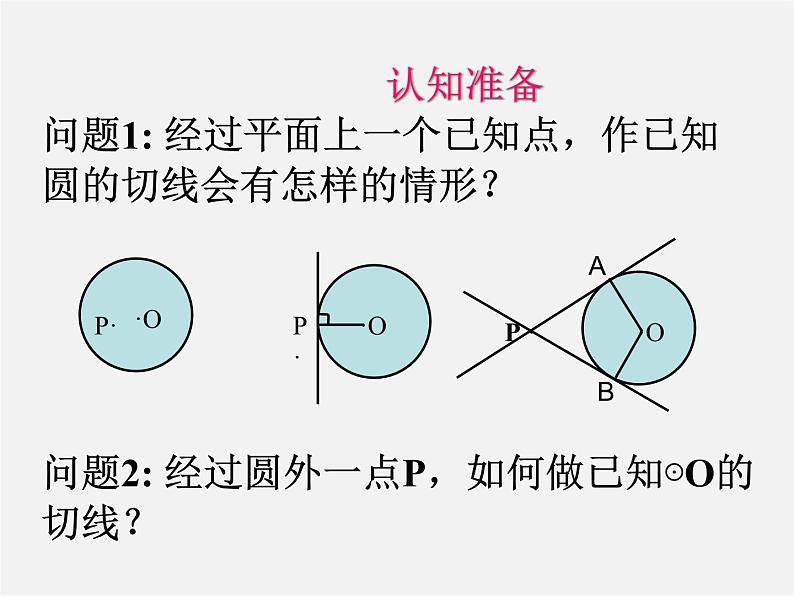
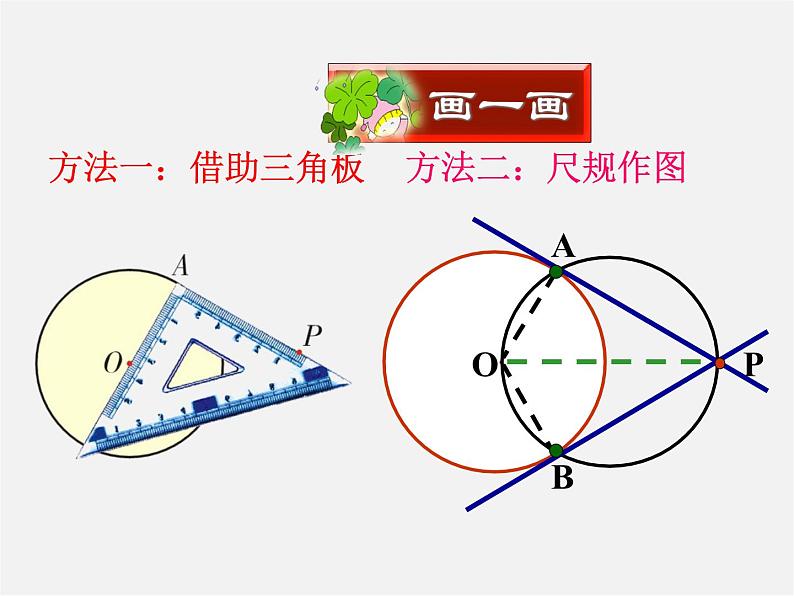
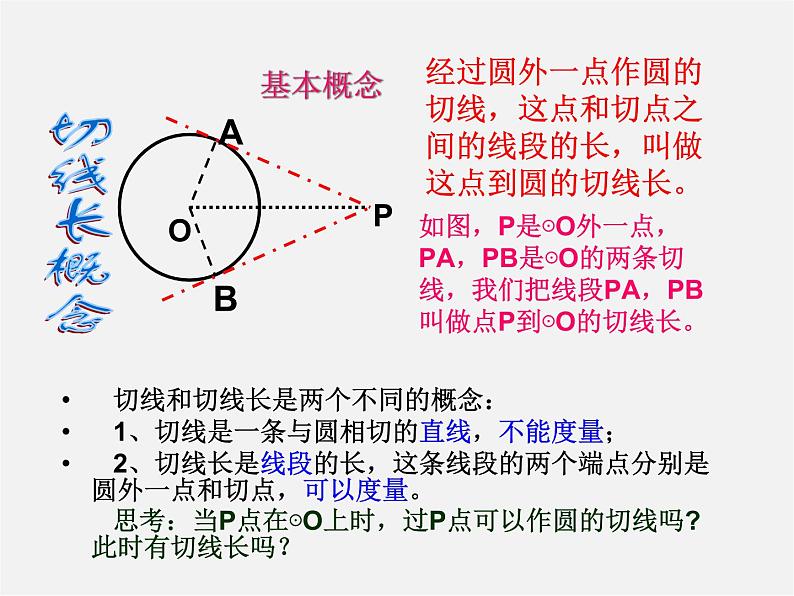
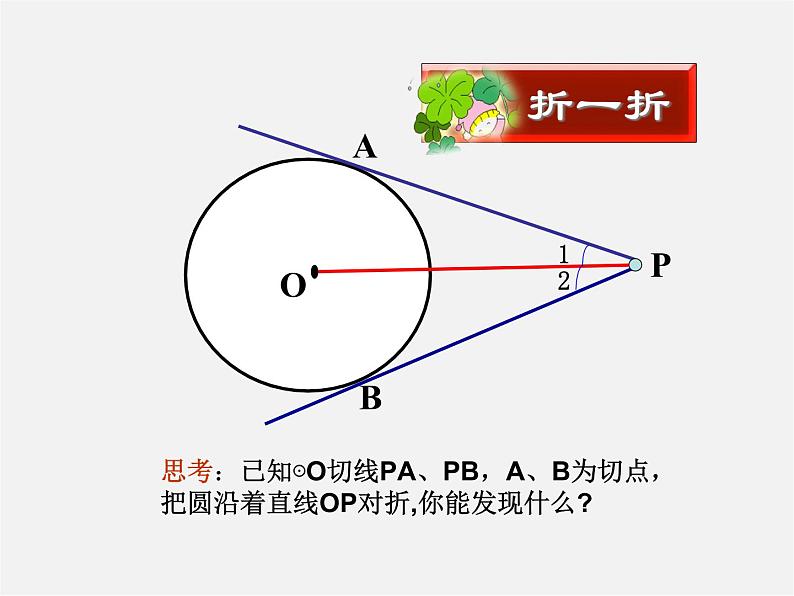
九年级数学备课组29.4切线长定理2014年12月5日问题1: 经过平面上一个已知点，作已知圆的切线会有怎样的情形？P ·P·P ·问题2: 经过圆外一点P，如何做已知⊙O的切线？AB认知准备 ·方法一：借助三角板方法二：尺规作图PABO切线长概念如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长。经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长。 切线和切线长是两个不同的概念： 1、切线是一条与圆相切的直线，不能度量； 2、切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。 思考：当P点在⊙O上时，过P点可以作圆的切线吗?此时有切线长吗？基本概念思考：已知⊙O切线PA、PB，A、B为切点，把圆沿着直线OP对折,你能发现什么? 若从⊙O外的一点引两条切线PA，PB，切点分别是A、B，连结OA、OB、OP，你能发现什么结论？并证明你所发现的结论。PA = PB，∠OPA=∠OPB试用文字语言叙述你所发现的结论P证明：∵PA，PB与⊙O相切，点A，B是切点 ∴OA⊥PA，OB⊥PB 即∠OAP=∠OBP=90° ∵ OA=OB，OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB ∠OPA=∠OPB证一证PA、PB与⊙O分别相切于点A、BPA = PB∠OPA=∠OPB几何语言:反思：切线长定理为证明线段相等、角相等提供新的方法从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。 切线长定理APOB1.若连结两切点A、B，AB交OP于点M.你又能得出什么新的结论？并给出证明.OP垂直平分AB证明：∵PA，PB是⊙O的切线,点A，B是切点 ∴PA = PB ∠OPA=∠OPB ∴△PAB是等腰三角形，PM为顶角的平分线 ∴OP垂直平分AB牛刀小试BPO。A2.若延长PO交⊙O于C点，连结AC、BC，你又能得出什么新的结论?并给出证明.AC=BC，证明：∵ PA，PB是⊙O的切线,点A，B是切点 ∴PA = PB，∠OPA=∠OPB ∵ PC=PC ∴△PCA ≌ △PCB ∴AC=BC，∠OCA=∠OCBC∠OCA=∠OCB牛刀再试 若PA、PB是⊙O的两条切线，A、B为切点，直线OP交于⊙O于点D、E，交AB于C。BAPOCED（3）写出图中所有的垂直关系OA⊥PA，OB ⊥PB，AB ⊥OP（5）写出图中所有的全等三角形△AOP≌ △BOP， △AOC≌ △BOC， △ACP≌ △BCP（4）写出图中所有的等腰三角形△ABP △AOB（1）写出图中所有相等的线段AO=BO=DO=EO，AP=BP，AC=BC（2）写出图中所有相等的弧AD=BD，AE=BE，DAE=DBE定理拓展。PBAO（3）连结圆心和圆外一点（2）连结两切点（1）分别连结圆心和切点反思：在解决有关圆的切线长问题时，往往需要我们构建基本图形，添加辅助线。归纳反思一、判断：（1）过任意一点总可以作圆的两条切线（ ）（2）从圆外一点引圆的两条切线，它们的长相等。（　　　）二、选择：如图所示，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8CM，则Δ PDE的周长为（ ）AABPDEOC1.切线长定理 从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPB切线长定理为证明线段相等，角相等，弧相等，垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结