初中数学北京课改版七年级上册第三章 简单的几何图形3.8 角平分线教课内容课件ppt

这是一份初中数学北京课改版七年级上册第三章 简单的几何图形3.8 角平分线教课内容课件ppt，

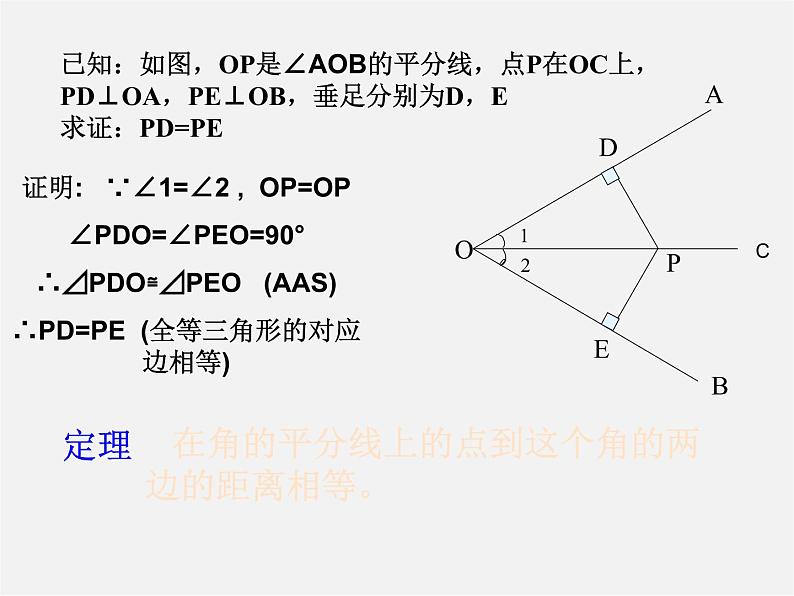
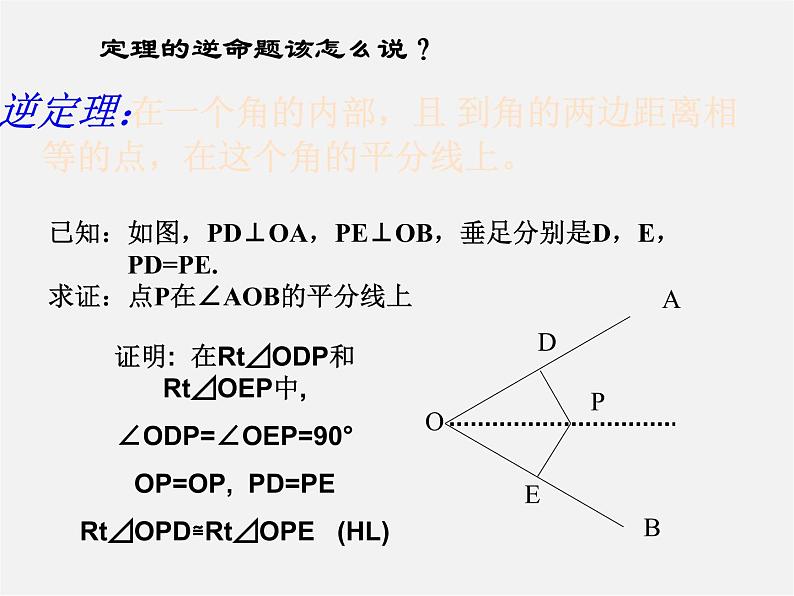
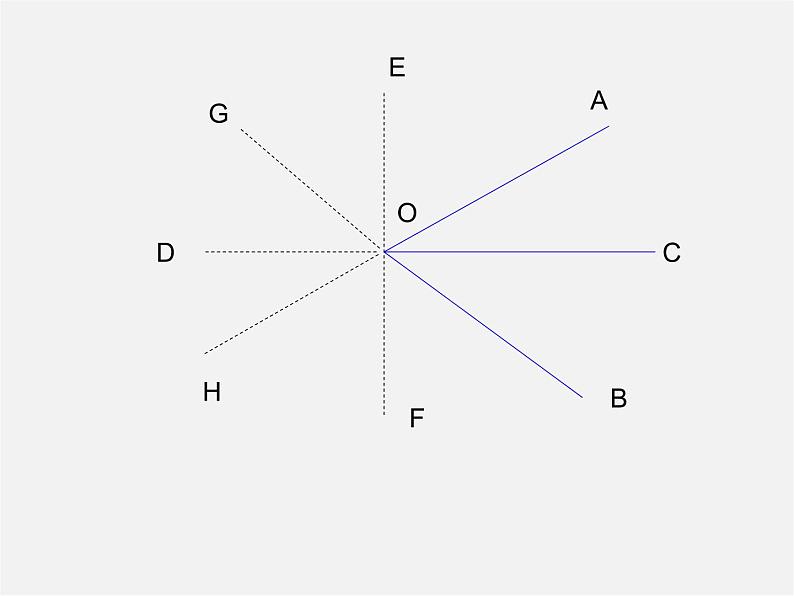
4.12角平分线 如图，浑南新区一个工厂，在公路西侧，到公路的距离与到河岸的距离相等，并且与河上公路桥较近桥头的距离为300米。你能尝试确定工厂的位置吗？并说明理由。 问题引入 问题探究角平分线性质 角的平分线上的点到这个角的两边的距离相等。已知：如图，OP是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E求证：PD=PE 在角的平分线上的点到这个角的两 边的距离相等。 ABOPDE12C定理证明: ∵∠1=∠2 , OP=OP∠PDO=∠PEO=90°∴⊿PDO≌⊿PEO (AAS)∴PD=PE (全等三角形的对应边相等) 定理的逆命题该怎么说？ 在一个角的内部，且 到角的两边距离相等的点，在这个角的平分线上。已知：如图，PD⊥OA，PE⊥OB，垂足分别是D，E， PD=PE.求证：点P在∠AOB的平分线上逆定理：证明: 在Rt⊿ODP和Rt⊿OEP中,∠ODP=∠OEP=90°OP=OP, PD=PERt⊿OPD≌Rt⊿OPE (HL)AOBCDEFGH尺规作图用尺规作角的平分线.已知:∠AOB求作:射线OC,使∠AOC=∠BOC数学问题源于生活实践，反过来数学又为生活实践服务OCP300m┒┓例1:例2: 已知：如图，E是∠BAC平分线上的一点，EB⊥AB，EC⊥AC，B，C分别是垂足。你能得到哪些结论？为什么？例3: 已知：如图所示：PA，PC分别是⊿ABC外角∠MAC与 ∠NCA平分线，它们交于P，PD⊥BM于M，PF⊥BN于F求证： 点P在∠MBN的平分线上E活动与探究:已知：如图，∠1=∠2，P为BN上一点，且PD⊥BC于D，AB+BC=2BD求证：∠BAP+∠BCP=180°123你有何收获?结束寄语严格性之于数学家,犹如道德之于人.证明的规范性在于：条理清晰，因果相应,言必有据.这是初学证明者谨记和遵循的原则.