




初中数学北京课改版九年级上册19.1 二次函数复习课件ppt
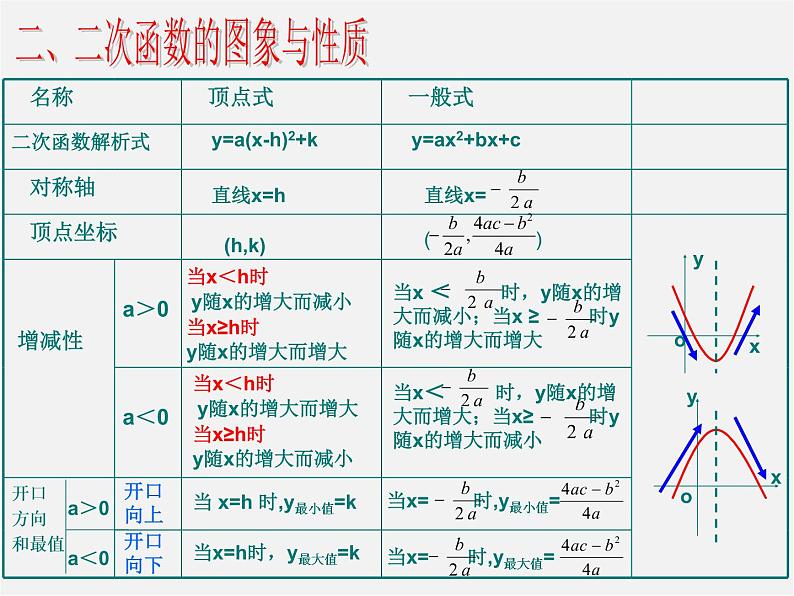
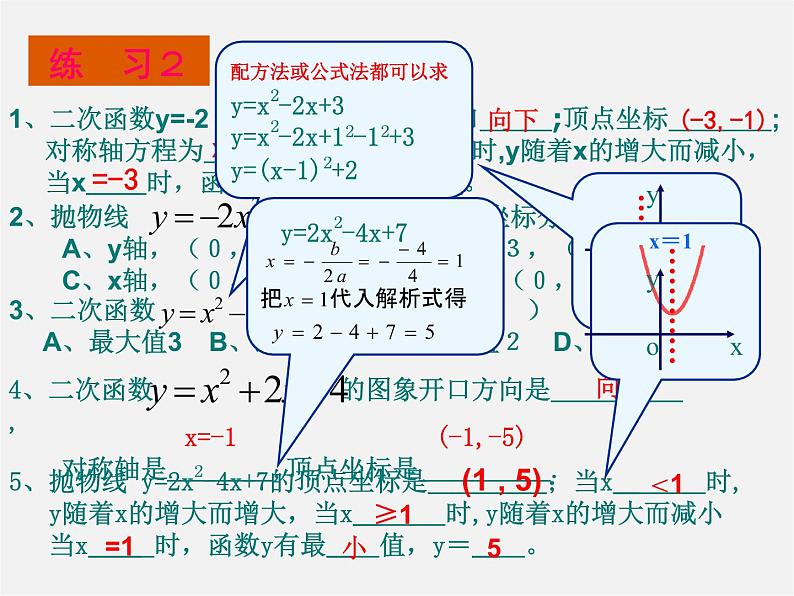
展开二 次 函 数复习(一)一、二次函数的概念函数y= (a、b、c为常数,______)叫做二次函数ax2+bx+ca ≠0(1)等式右边关于自变量x的代数式一定是判断一个函数是否是二次函数满足的条件:(2)化简后等式的右边自变量x最高次数为整式2(3)化简后等式的右边二次项系数a≠0 D、 y=3(x-1)²+1B、y=mx2+3x-1 A、y=(x+3)²-x²1.下列函数中是二次函数( )练 习1D2.如果函数 是二次函数, 那么m= .-2k1=0 k2=30m≠0二、二次函数的图象与性质y=a(x-h)2+ky=ax2+bx+c直线x=h直线x=(h,k)( ) 当x < 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大当x< 时,y随x的增大而增大;当x≥ 时y随x的增大而减小当 x=h 时,y最小值=k当x= 时,y最小值=当x=h时,y最大值=k当x= 时,y最大值=yxooyx当x<h时 y随x的增大而减小当x≥h时y随x的增大而增大当x<h时 y随x的增大而增大当x≥h时y随x的增大而减小a>0a<0开口向上开口向下1、二次函数y=-2(x+3)2-1 图象的开口 ;顶点坐标 ; 对称轴方程为 ;当x 时,y随着x的增大而减小, 当x 时,函数y有最 值是 。(-3,-1)练 习2Dx=-3向上x=-1 (-1,-5)5、抛物线 y=2x2-4x+7的顶点坐标是 ;当x 时, y随着x的增大而增大,当x 时,y随着x的增大而减小 当x 时,函数y有最 值,y= 。(1 , 5)B向下≥-3 大 -1 =-3<1 ≥1 =1 小 5配方法或公式法都可以求y=x2-2x+3y=x2-2x+12-12+3y=(x-1)2+2y=2x2-4x+7Bk+2>0k²+k-4=2k1=-3 k2=2k>-2∴k=2∴k+2>028、若抛物线y=x2+2x+ k的顶点在x轴 下方,则k的取值范 围是 k 。k-1<0<1配方法:y=x2+2x+12-12+k=(x+1)2+k-1k-1<0变式、抛物线y=x2+2x+ k的顶点在x轴上,则k 。=1三、二次函数y=ax2+bx+c(a≠0)的系数a,b, c,△与抛物线图象的关系a决定开口方向:a>0时开口向上, a<0时开口向下a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧 a、b异号时对称轴在y轴右侧 b=0时对称轴是y轴c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴 c=0时抛物线过原点 c<0时抛物线交于y轴的负半轴△决定抛物线与x轴的交点:△>0时抛物线与x轴有两个交点 △=0时抛物线与x轴有一个交点 △<0时抛物线与x轴没有交点(上正、下负)(左同、右异) (上正、下负)△= b2-4ac 1、二次函数y=ax2+bx+c(a≠0)的图象如图 所示,则a、b、c的符号为( ) A、a<0,b>0,c>0 B、a<0,b>0,c<0 C、a<0,b<0,c>0 D、a<0,b<0,c<0 2、二次函数y=ax2+bx+c(a≠0)的图象 如图所示,则a、b、c的符号为( ) A、a>0,b>0,c=0 B、a<0,b>0,c=0 C、a<0,b<0,c<0 D、a>0,b<0,c=0 3、二次函数y=ax2+bx+c(a≠0)的图象如图 所示,则a、b、c 、 △的符号为( ) A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0 C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0 BACooo练习3:熟练掌握a,b, c,△与抛物线图象的关系(上正、下负)(左同、右异) ·c4.抛物线y=ax2+bx+c(a≠0)的图象经过原点和 二、三、四象限,判断a、b、c的符号情况: a 0,b 0,c 0. <=<5.抛物线y=ax2+bx+c(a≠0)的图象经过原点, 且它的顶点在第三象限,则a、b、c满足 的条件是:a 0,b 0,c 0. >=[1999中考]6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0, 那么这个二次函数图象的顶点必在第 象限 先根据题目的要求画出函数的草图,再根据图象以及性质确定结果(数形结合的思想)[2000中考]四>-2二次函数y=ax2+bx+c(a≠0)的几个特例: 1、当x=1 时, 2、当x= -1时, 3、当x=2时, 4、当x= -2时,y=a+b+c y=a-b+cy=4a+2b+cy=4a-2b+cxyo1-12 二次函数y=ax2+bx+c(a≠0)的图象如上图所示, 那么下列判断正确的有 (填序号) .①abc>0 ②b2-4ac<0 ③2a=-b ④a+b+c<0⑤a-b+c>0 ⑥4a+2b+c<0 ⑦4a-2b+c<0. ③⑦a<0b>0,c>0例题在判断a+b+c,a-b+c, 4a+2b+c,4a-2b+c等式子的符号时需要整体考虑,结合图象观察x取相应值时y值在正半轴还是负半轴对于b与2a的关系式通常需要结合图象考虑对称轴的值判断×-1××××x=11、二次函数y=ax2+bx+c(a≠0)的图象 如图所示,下列判断不正确 的是( ) A、abc>0, B、b2-4ac<0, C、a-b+c<0, D、4a+2b+c>0. DC练习4:与y轴的交点(0,c)a< 0a< 0a>0a<0ABCX=-2(-3,0)(-1,0)(-2,-1)(0,3)已知二次函数y=x2+4x+3,回答下列问题:(1)说出此抛物线的对称轴 和顶点坐标 ;(2)抛物线与x轴的交点A、B的坐标, 与y轴的交点C的坐标;(3)函数的最值和增减性;(4)x取何值时① y<0 ;②y>0四、求二次函数y=ax2+bx+c与坐标轴的交点:图象与x轴的交点令y=0 ax2+bx+c=0图象与y轴的交点令x=0 y =c当 时,y>0,当 时,y<0.-3
北京课改版九年级上册21.3 圆的对称性课文ppt课件: 这是一份北京课改版九年级上册21.3 圆的对称性课文ppt课件,
北京课改版九年级上册第二十一章 圆(上)21.4 圆周角教课ppt课件: 这是一份北京课改版九年级上册第二十一章 圆(上)21.4 圆周角教课ppt课件,
初中北京课改版21.1 圆的有关概念教课内容课件ppt: 这是一份初中北京课改版21.1 圆的有关概念教课内容课件ppt,













