初中数学华师大版八年级上册14.2 勾股定理的应用多媒体教学课件ppt

这是一份初中数学华师大版八年级上册14.2 勾股定理的应用多媒体教学课件ppt，共16页。PPT课件主要包含了变式训练，实际应用3，在Rt△AOB中，在Rt△COD中，实际应用4，如何构造直角三角形，想一想，名题鉴赏，基础训练，过A作AE⊥BC于E等内容，欢迎下载使用。
勾股定理及其数学语言表达式:
直角三角形两直角边a、b的平方和等于斜边c的平方。
在△ABC中，AB=c, BC=a, AC=b, ∠B=90°.
(1)若c=24，b=25，则a= ;
(2)若a=6，b=10，则c = ;
例 在Rt△ABC中，∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c，若 a﹕b=3﹕4, c=15.求a、b.
通过设未知数，根据勾股定理列出方程求出a、b.
∴a=9, b=12.
设 a=3x, b=4x .
在Rt△ABC中，∠C=90°,
由勾股定理，得：a2+b2=c2
即：9x2+16x2=225
解得：x2=9 ∴x=3 (负值舍去)
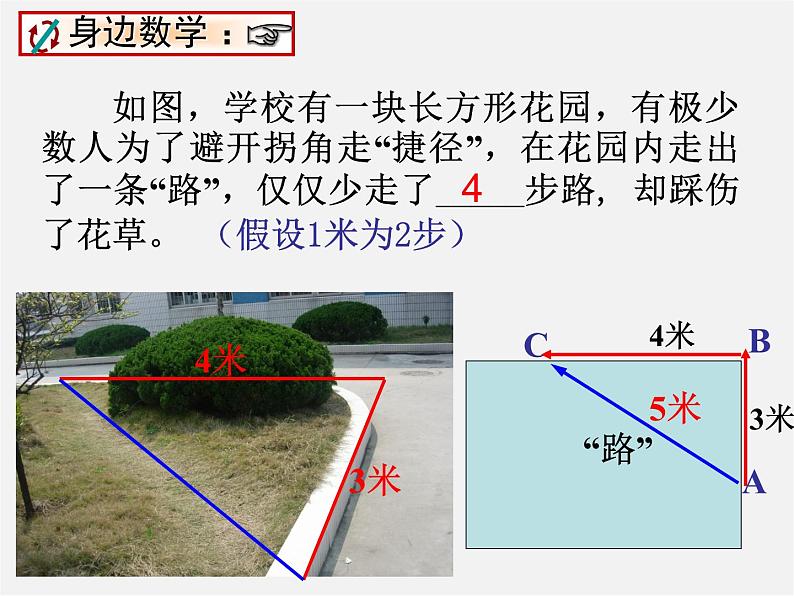
如图，学校有一块长方形花园，有极少数人为了避开拐角走“捷径”，在花园内走出了一条“路”，仅仅少走了_____步路, 却踩伤了花草。 （假设1米为2步）
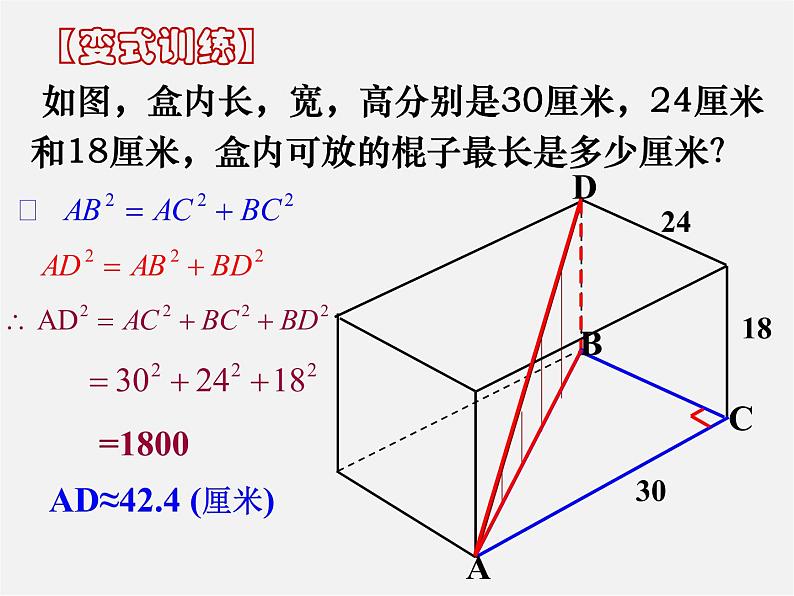
如图，盒内长，宽，高分别是30厘米，24厘米和18厘米，盒内可放的棍子最长是多少厘米？
AD≈42.4 (厘米)
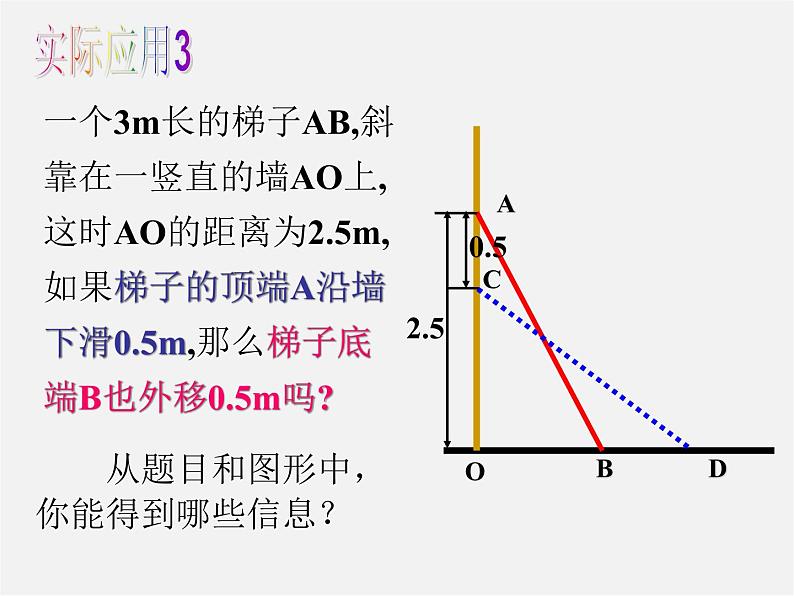
一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
从题目和图形中，你能得到哪些信息？
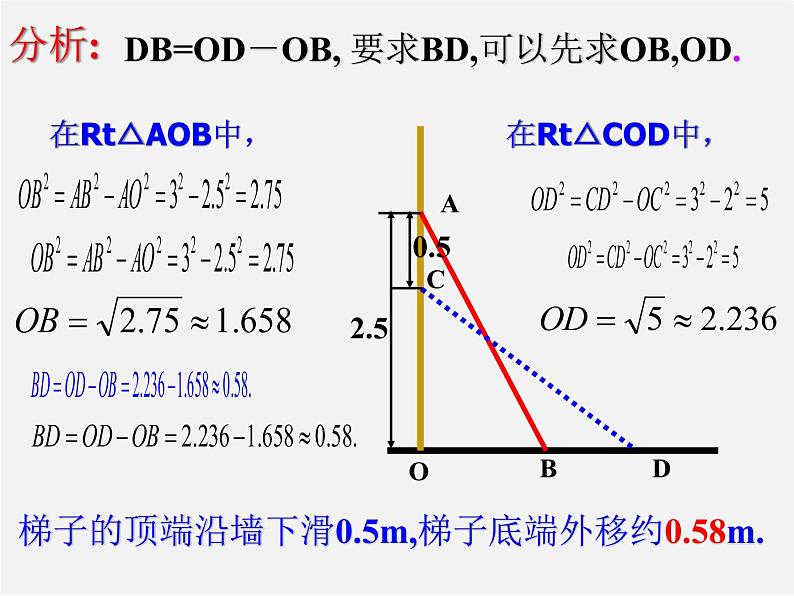
梯子的顶端沿墙下滑0.5m,梯子底端外移约0.58m.
DB=OD－OB, 要求BD,可以先求OB,OD.
如图，求矩形零件上两孔中心A、B的距离.
小明的妈妈买了一部29英寸（74厘米）的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你能解释这是为什么吗？
荧屏对角线大约为74厘米
我们通常所说的29英寸或74厘米的电视机，是指其荧屏对角线的长度
《九章算术》中：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，请问这个水的深度与这根芦苇的长度各是多少？
1、一个直角三角形中两边长分别为3和4，则另一边长为 。
2、在Rt△ABC中，∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c，若 a﹕c=3﹕5, b=20. 则a=____，c=___ .
3、如图，小方格都是边长为1的正方形，求四边形ABCD的面积与周长.（精确到0.1）
1. 如图，在△ABC中，AB=AC，D点在CB延长线上，求证：AD2－AB2 =BD·CD
∵AB=AC，∴BE=CE
AD2=AE2+DE2
AB2=AE2+BE2
∴ AD2－AB2=(AE2+DE2)－(AE2+BE2)
= (DE+BE)·( DE－BE)
= (DE+CE)·( DE－BE)
2. 如图，∠ACB=∠ABD=90°，CA=CB，
∵∠ABD=90°，∠DAB=30°
∠DAB=30°，AD=8，求AC的长。
谈谈你这节课的收获有哪些?
2.会用勾股定理解决简单应用题.
1.学会了构造直角三角形．