2021学年3 角平分线评课课件ppt

这是一份2021学年3 角平分线评课课件ppt，共10页。PPT课件主要包含了情境问题，3验证猜想，逆命题等内容，欢迎下载使用。

不利用工具，请你将一张用纸片做的角分成两个相等的角。你有什么办法？
再打开纸片 ，看看折痕与这个角有何关系？
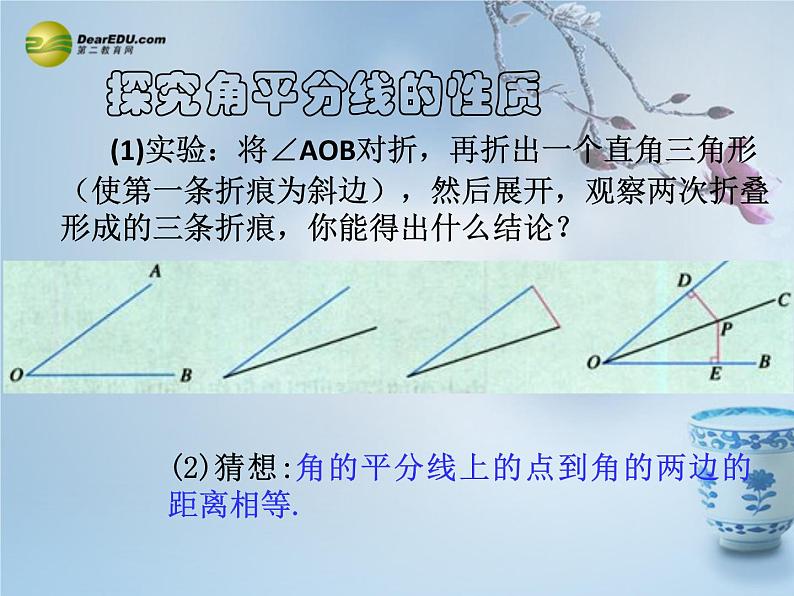
(1)实验：将∠AOB对折，再折出一个直角三角形（使第一条折痕为斜边），然后展开，观察两次折叠形成的三条折痕，你能得出什么结论？
(2)猜想:角的平分线上的点到角的两边的距离相等.
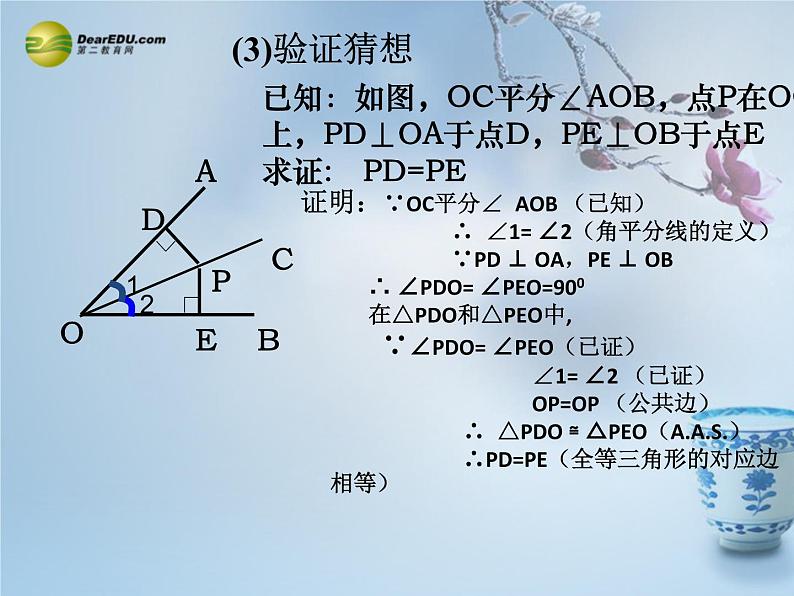
证明：∵OC平分∠ AOB （已知） ∴ ∠1= ∠2（角平分线的定义） ∵PD ⊥ OA，PE ⊥ OB ∴ ∠PDO= ∠PEO=900 在△PDO和△PEO中, ∵∠PDO= ∠PEO（已证） ∠1= ∠2 （已证） OP=OP （公共边） ∴ △PDO ≌ △PEO（） ∴PD=PE（全等三角形的对应边相等）
已知：如图，OC平分∠AOB，点P在OC上，PD⊥OA于点D，PE⊥OB于点E求证: PD=PE
此性质的推理过程:
∵ ∠1= ∠2, PD ⊥ OA， PE ⊥ OB（已知）∴PD=PE（角平分线上的点到角两边的距离相等）
(4)得到角平分线的性质：
角平分线上的点到角两边的距离相等。
判断题（ ）∵ 如图，AD平分∠BAC（已知）
∴BD = DC ( )
角的平分线上的点到角的两边的距离相等。
如图，在Rt△ABC 中，
角平分线的性质，为我们证明两条线段相等 又提供了新的方法与途径。
DE⊥AB，垂足为E，
∵ BD是∠ABC的平分线
已知：如图,PD⊥OA，PE⊥OB，点D、E为垂足，PD＝PE．求证：点P在∠AOB的平分线上．
证明： ∵PD⊥OA，PE⊥OB，
在Rt △PDO 与Rt △PEO中
∴∠PDO= ∠PEO=900
∴Rt△PDO≌ Rt △PDO(H.L.)
∴∠1=∠2 即点P在∠AOB的平分线上
到一个角的两边的距离相等的点在这个角的平分线上.
如图，在△ABC的 顶点 B的外角的平分线BD与顶点 C的外角的平分线CE相交于点P．求证：点Ｐ到三边AB、BC、AC的距离相等．
证明：过点P作PM、PK、 PH分别垂直于AB、BC、AC，垂足为M、K、H。∵BD平分∠CBM ∴PK＝PM同理PK＝PH∴PK＝PM＝PH即点P到三边AB、BC、AC的距离相等
若求证点P在∠BAC的平分线上，又该如何证明呢？