北京161中2020-2021学年九年级（上）期中数学试卷（word版无答案）

2020-2021学年北京161中九年级（上）期中数学试卷

一、选择题：（本题共16分，每小题2分）在每小题给出的四个选项中，只有一项符合题目的要求．

1．二次函数y＝﹣（x﹣1）2+3图象的顶点坐标是（　　）

A．（1，3） B．（﹣1，3） C．（﹣1，﹣3） D．（1，﹣3）

2．已知⊙O的半径为3cm，点P到圆心O的距离OP＝2cm，则点P在（　　）

A．在⊙O外 B．在⊙O上 C．在⊙O内 D．不能确定

3．如图，点A、B、C都在⊙O上，若∠AOB＝72°，则∠ACB的度数是（　　）

A．18° B．36° C．30° D．72°

4．若要得到函数y＝（x+1）2+2的图象，只需将函数y＝x2的图象（　　）

A．先向右平移1个单位长度，再向上平移2个单位长度 

B．先向左平移1个单位长度，再向下平移2个单位长度 

C．先向左平移1个单位长度，再向上平移2个单位长度 

D．先向右平移1个单位长度，再向下平移2个单位长度

5．如图，△ABC中，∠BAC＝80°，AB＝4，AC＝6．甲、乙、丙、丁四名同学分别在△ABC内画出一个阴影三角形与△ABC相似，其中画错误的是（　　）

A．甲 B．乙 C．丙 D．丁

6．关于x的一元二次方程（a﹣5）x2﹣4x﹣1＝0有实数根，则a满足（　　）

A．a≥1 B．a＞1且a≠5 C．a≥1且a≠5 D．a≠5

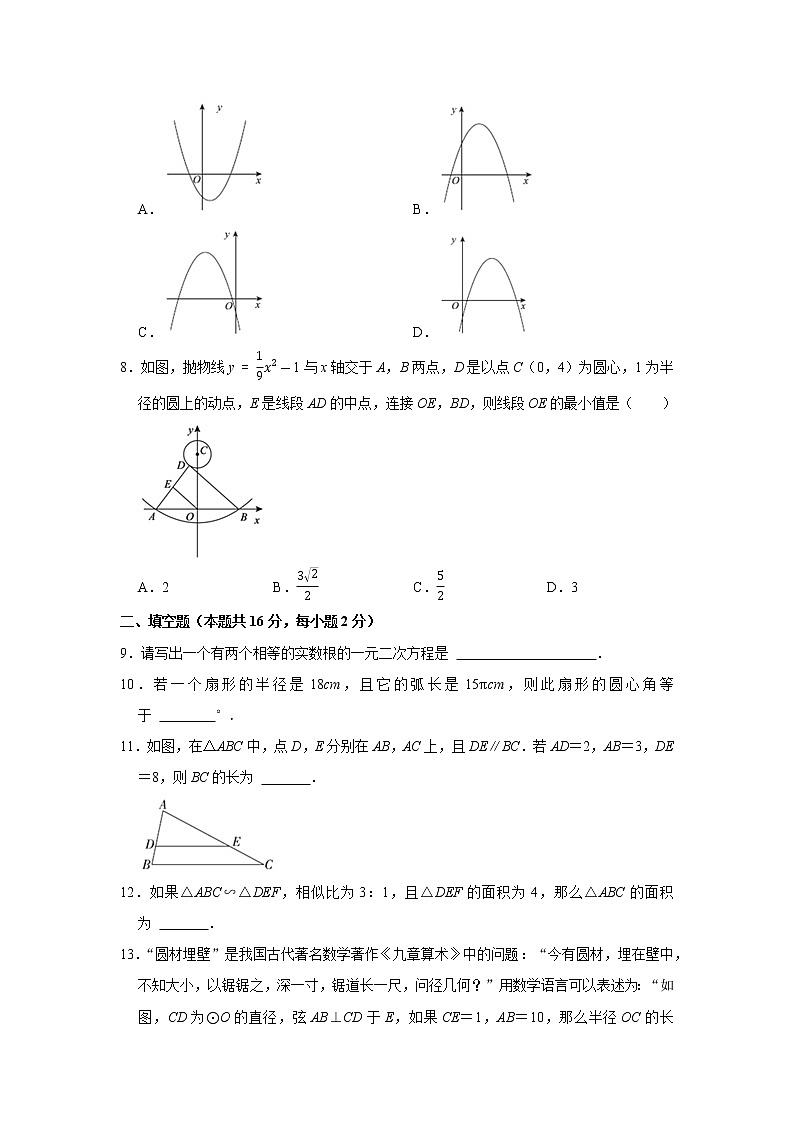
7．已知函数y＝﹣x2+bx+c，其中b＞0，c＜0，此函数的图象可以是（　　）

A． B． 

C． D．

8．如图，抛物线y1与x轴交于A，B两点，D是以点C（0，4）为圆心，1为半径的圆上的动点，E是线段AD的中点，连接OE，BD，则线段OE的最小值是（　　）

A．2 B． C． D．3

二、填空题（本题共16分，每小题2分）

9．请写出一个有两个相等的实数根的一元二次方程是 　                　．

10．若一个扇形的半径是18cm，且它的弧长是15πcm，则此扇形的圆心角等于 　    　°．

11．如图，在△ABC中，点D，E分别在AB，AC上，且DE∥BC．若AD＝2，AB＝3，DE＝8，则BC的长为 　   　．

12．如果△ABC∽△DEF，相似比为3：1，且△DEF的面积为4，那么△ABC的面积为 　   　．

13．“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可以表述为：“如图，CD为⊙O的直径，弦AB⊥CD于E，如果CE＝1，AB＝10，那么半径OC的长为 　   　．”

14．直线y＝x+m和抛物线y＝x2+bx+c都经过点A（1，0），B（3，2）观察图象直接写出不等式x2+bx+c＜x+m的解集 　      　．

15．方程2x2﹣3x﹣1＝0的两根为x1，x2，则的值为 　   　．

16．如图所示的网格是正方形网格，线段AB绕点A顺时针旋转α（0°＜α＜180°）后，直线AB与⊙O相切，则α的值为 　         　．

三、解答题（本题共68分，第17--20题，每小题5分，第21题6分，第22题5分，第23题6分，第24题5分，第25题6分，第26题6分，第27--28题，每小题5分.）解答应写出文字说明、演算步骤或证明过程.

17．解方程：（1）x（x﹣2）＝0；

               （2）x2+2x﹣5＝0．

18．下面是小文设计的“过圆外一点作圆的切线”的作图过程．已知：⊙O和圆外一点P．求作：过点P的⊙O的切线．作法：①连接OP；②以OP为直径作⊙M，交⊙O于点A，B；③作直线PA，PB；所以直线PA，PB为⊙O的切线．根据小文设计的作图过程，

（1）使用直尺和圆规，按上述作法 补全图形；（保留作图痕迹）

（2）完成下面的证明．

证明：连接OA，OB．

∵OP为⊙M的直径，

∴∠OAP＝∠OBP＝90° 　 　（填推理的依据）．

∴OA⊥AP，OB⊥BP．

∵OA，OB为⊙O半径，

∴直线PA，PB为⊙O的切线． 　 　（填推理的依据）．

19．已知：如图，AB为⊙O的直径，OD∥AC．求证：点D平分．

20．抛物线y＝ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表：

（1）写出该抛物线的对称轴及顶点坐标；

（2）求出抛物线y＝ax2+bx+c的解析式，并在平面直角坐标系中画出该抛物线的图象；

（3）结合图象回答：

①不等式ax2+bx+c＜0的解集是 　 　；

②当﹣1＜x＜2时，y的取值范围是 　 　．

21．如图，是一座古代拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．经过讨论，同学们得出三种建立平面直角坐标系的方案（如下图），你选择的方案是 　 　（填方案一，方案二，或方案三），则B点坐标是 　 　．

（1）求出你所选方案中的抛物线的表达式；

（2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．

22．如图，在△ABC中，AD平分∠BAC，E是AD上一点，且BE＝BD．

（1）求证：△ABE∽△ACD；

（2）若BD＝1，CD＝2，求的值．

23．已知关于x的一元二次方程x2﹣mx+m﹣1＝0．

（1）求证：方程总有两个实数根；

（2）若方程有一个根为负数，求m的取值范围．

24．如图，AB为⊙O的直径，C为⊙O上一点，⊙O的切线BD交OC的延长线于点D．

（1）求证：∠DBC＝∠OCA；

（2）若∠BAC＝30°，AC＝2．求CD的长．

25．关于x的一元二次方程ax2+bx+c＝0（a＞0）有两个不相等且非零的实数根，探究a，b，c满足的条件．小华根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小华的探究过程：第一步：设一元二次方程ax2+bx+c＝0（a＞0）对应的二次函数为y＝ax2+bx+c（a＞0）；第二步：借助二次函数图象，可以得到相应的一元二次方程中a，b，c满足的条件，列表如下：

（1）请帮助小华将上述 表格补充完整；

（2）参考小华的做法，解决问题：

若关于x的一元二次方程x2﹣（m+5）x﹣2m＝0有一个负实根和一个正实根，且负实根大于﹣1，求实数m的取值范围．

26．在平面直角坐标系xOy中，抛物线C1：y＝mx2+2mx+m﹣1沿x轴翻折得到抛物线C2．

（1）求抛物线C2的顶点坐标；

（2）横、纵坐标都是整数的点叫做整点．

①当m＝1时，求抛物线C1和C2围成的封闭区域内（包括边界）整点的个数；

②如果抛物线C1和C2围成的封闭区域内（包括边界）恰有7个整点，求出m的取值范围．

27．已知：在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC边中点．点M为线段BC上的一个动点（不与点C，点D重合），连接AM，将线段AM绕点M顺时针旋转90°，得到线段ME，连接EC．

（1）如图1，若点M在线段BD上．

①依据题意补全图1；

②求∠MCE的度数．

（2）如图2，若点M在线段CD上，请你补全图形后，直接用等式表示线段AC、CE、CM之间的数量关系．

28．如图1，已知线段AB与点P，若在线段AB上存在点Q，满足PQ≤AB，则称点P为线段AB的“限距点”．

（1）如图2，在平面直角坐标系xOy中，若点A（﹣1，0），B（1，0）．

1．在C（0，2），D（﹣2，﹣2），E（1，）中，是线段AB的“限距点”的是 　 　；

2．点P是直线y＝x+1上一点，若点P是线段AB的“限距点”，请求出点P横坐标xp的取值范围．

（2）在平面直角坐标系xOy中，点A（t，1），B（t，﹣1），直线yx+2与x轴交于点M，与y轴交于点N．若线段MN上存在线段AB的“限距点”，请求出t的取值范围．