
2021-2022学年武汉市新洲区邾城街九年级上学期期中数学试卷(word版无答案)
展开2021-2022学年武汉市新洲区邾城街九年级(上)期中数学试卷
一、选择题(共10小题,每小题3分,共30分)
1.将方程3x(x﹣1)=5(x+2)化成一元二次方程的一般形式后,一次项系数是( )
A.3 B.﹣8x C.﹣8 D.﹣10
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.抛物线y=(x﹣6)2+3的顶点坐标为( )
A.(6,3) B.(﹣6,3) C.(3,3) D.(﹣3,)
4.方程2x2﹣3x﹣=0的根的情况为( )
A.两个相等的实数根 B.两个不相等的实数根
C.没有实数根 D.只有一个实数根
5.将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的拋物线为( )
A.y=(x+3)2+5 B.y=(x﹣3)2+5 C.y=(x+5)2+3 D.y=(x﹣5)2+3
6.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.20° C.24° D.28°
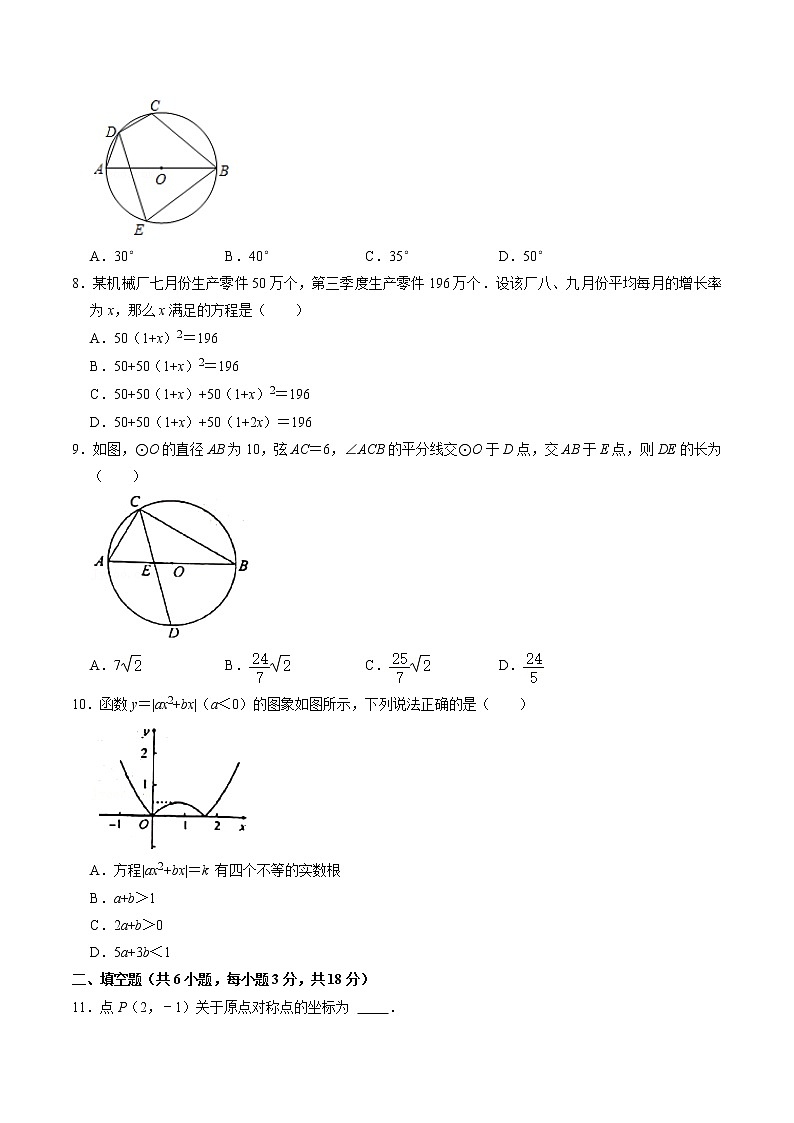
7.如图,AB为⊙O的直径,点C、D、E在⊙O上,且=,∠E=70°,则∠ABC的度数为( )
A.30° B.40° C.35° D.50°
8.某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=196
B.50+50(1+x)2=196
C.50+50(1+x)+50(1+x)2=196
D.50+50(1+x)+50(1+2x)=196
9.如图,⊙O的直径AB为10,弦AC=6,∠ACB的平分线交⊙O于D点,交AB于E点,则DE的长为( )
A.7 B. C. D.
10.函数y=|ax2+bx|(a<0)的图象如图所示,下列说法正确的是( )
A.方程|ax2+bx|=k 有四个不等的实数根
B.a+b>1
C.2a+b>0
D.5a+3b<1
二、填空题(共6小题,每小题3分,共18分)
11.点P(2,﹣1)关于原点对称点的坐标为 .
12.若关于x的一元二次方程ax2=b(a≠0)一根为2,则另一根为 .
13.把一个物体从地面以10m/s速度竖直上抛,那么物体经过x(s)时,离地面高度为h(m),h与x的函数关系为h=10x﹣4.9x2,则物体回到地面的时间为 s.
14.芳芳家今年搬进了新房,新房外的凉台呈圆弧形,如图所示,她测得凉台的宽度AB为8m,凉台的最外端C点离AB的距离CD为2m,则凉台所在圆的半径为 m.
15.已知关于x的一元二次方程(x﹣3)(x﹣2)﹣p2=0,下列结论:①方程总有两个不等的实数根;②若两个根为x1,x2,且x1>x2,则x1>3,x2<3;③若两个根为x1,x2,则(x1﹣2)(x2﹣2)=(x1﹣3)(x2﹣3);④若x=(p为常数),则代数式(x﹣3)(x﹣2)的值为一个完全平方数,其中正确的结论是 .
16.如图,∠ABC=90°,AC=6,以AB为边长向外作等边△ABM,连CM,则CM的最大值为 .
三、解答题(共8小题,共72分)
17.解方程:x2﹣4x﹣7=0.
18.用一段长为30m的篱笆围成一个靠墙的矩形菜园,墙的长度为18m.
(1)设垂直于墙的一边长为xm,则是菜园的面积为 ;
(2)若菜园的面积为100m2,求x的值.
19.如图,点A、P、B、C为⊙O上四点,∠APC=∠CPB=60°.
(1)判断△ABC形状并证明;
(2)将△APB绕点B顺时针旋转60°至△CMB,请画出图形,直接写出PA,PB,PC三者之间的数量关系 .
20.如图,在8×8的正方形网格中,点A,B,C,P都在格点上,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线表示,画图结果用实线表示).
(1)△ABC的形状为 ;
(2)在图1中将线段BC绕点B逆时针旋转90°,画出图形;
(3)在图1中在AC上找一点M,使∠AMP=45°;
(4)在图2中作PN⊥AC,且PN=AC,若AC绕某一点旋转得到PN(P与C对应),在图中标出旋转中心O.
21.如图,AB为⊙O的直径,点C为的中点,CD⊥AE交直线AE于D点.
(1)求证:OC∥AD;
(2)若DE=1,CD=2,求⊙O的直径.
22.甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出,如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元.
乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;②月利润=月租车费﹣月维护费;③两公司月利润差=月利润较高公司的利润﹣月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是 元;
(2)当每个公司租出的汽车为 辆时,两公司的月利润相等;
(3)求两公司月利润差的最大值.
23.问题背景:(1)如图1,等边△ABC,点P在△ABC左侧且∠APC=30°,将△APC绕点A顺时针旋转60°,画出图形.
探究思考:(2)在(1)的条件下,求证:PB=AC;
拓展创新:(3)如图2,等边△ABC,∠AMC=60°,AM=6,CM=4,直接写出BM的长 .
24.已知抛物线y=ax2+bx﹣2与x轴交于点A(﹣1,0),B(4,0),与y轴交于C点.
(1)求抛物线的解析式;
(2)如图1,直线x=m(0<m<4)交抛物线于M点,交BC于N点,且CM∥ON,求m的值;
(3)如图2,若点P为抛物线x轴下方一点,直线AP交y轴于M点,直线BP交y轴于N点,且OM•ON=,求P点坐标.
湖北省武汉市新洲区邾城街2023一2024学年上学期八年级期中数学试题: 这是一份湖北省武汉市新洲区邾城街2023一2024学年上学期八年级期中数学试题,共6页。
2022-2023学年湖北省武汉市新洲区邾城街九年级(下)月考数学试卷(3月份)(含解析): 这是一份2022-2023学年湖北省武汉市新洲区邾城街九年级(下)月考数学试卷(3月份)(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年湖北省武汉市新洲区邾城街九年级(下)月考数学试卷(3月份)(含解析): 这是一份2022-2023学年湖北省武汉市新洲区邾城街九年级(下)月考数学试卷(3月份)(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












